机器学习(一)基本概念
- 13 10 月, 2023
- by
- pladmin
一、概述
1.1 机器学习解决的问题
机器学习本质上就是一个庞大的函数式,主要能解决的问题有:regression(回归标量)、classification(选项/分类)、structured learning(模态生成)。
regression更偏向于预测结果,例如预测pm2.5、预测房价、预测股票等等;
classification更偏向于聚类划分,要给出一个具体的结果选项;
structured learning更偏向于图像、音频、视频、语句生成等任务。
1.2 机器学习的要素
机器学习的核心问题是,找到一个函数式,能够获得1.1所描述的各类问题的答案。例如:y = b + w_i * x就是一个完整的函数式,它可以根据输入的x、权重w_i和参数b来预测得到结果y。
所以可以看到,机器学习最关键的点就是:类似y = b + w_i * x这样的函数模型应该是什么样的,以及w_i应该取什么数值。对于前者的问题,就是要求我们设计出一个合适的、通用性高的函数结构(对于深度学习就是神经网络结构);对于后者的问题,就需要我们通过训练来找到最佳的w_i的取值。
那么如何评估 训练过程中的w_i是否合适呢?就需要引入loss的概念,loss就是用来计算 使用当前权重w_i来测试,得到的结果与正确结果之间的差值。因为要测试的数据很多,所以最后我们会获得很多个差值,我们可以通过以下两种算法来得到最终的loss结果:
$$LOSS_{MAE} = \frac{1}{N}\sum (|y_{result} – y_{real}|)$$
$$LOSS_{MSE} = \frac{1}{N}\sum (|y_{result} – y_{real}|)^2$$
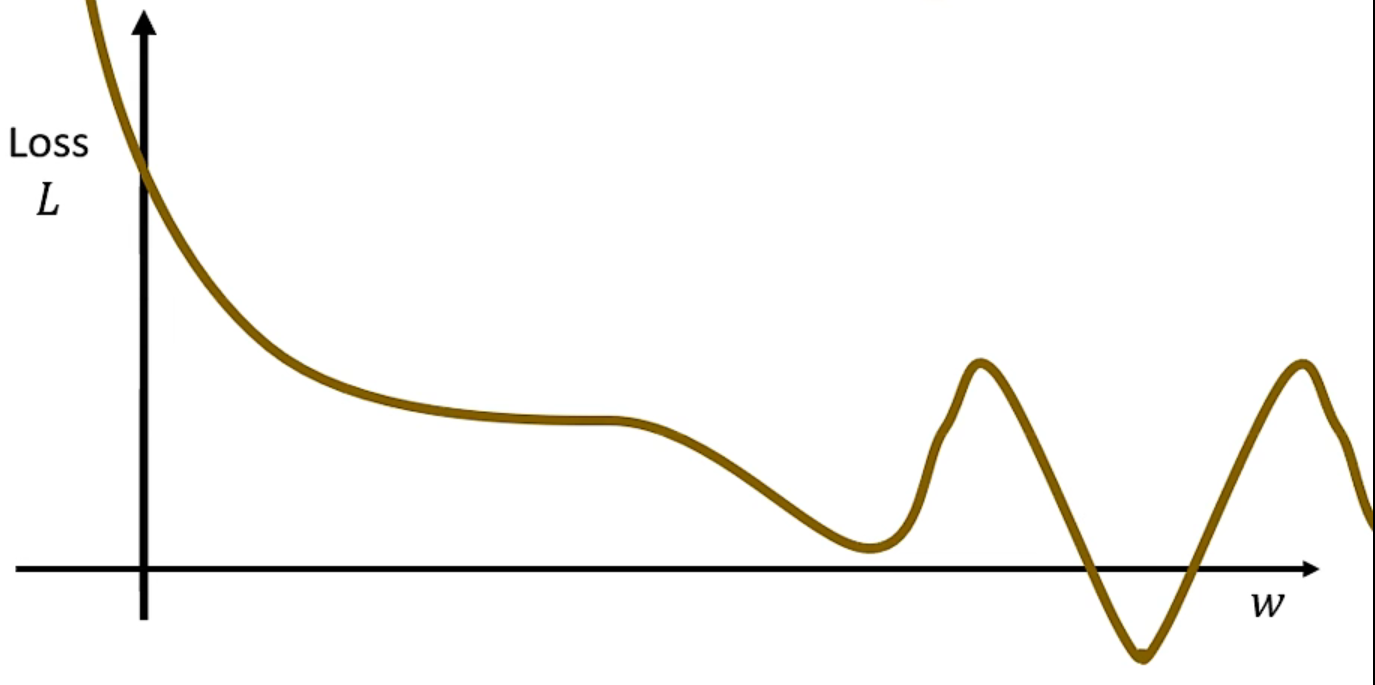
现在我们得到了loss值,也就得到了该组w_i的评估。但是要向哪个方向去调整w_i,才能让loss降低呢?我们观察一下这张图:
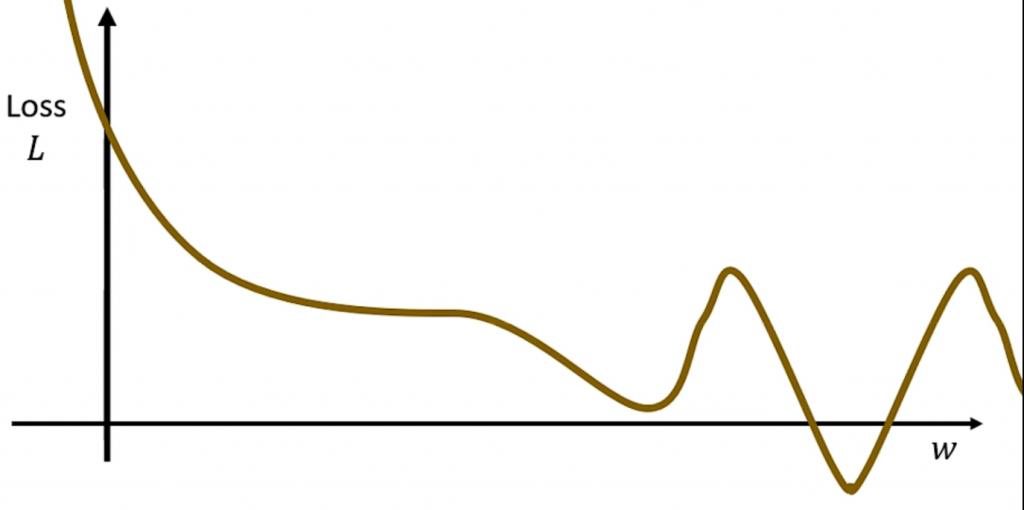
Loss值就是关于w_i的函数,假如当前的w=w_0,那么我们就可以计算出来该点 Loss关于w的梯度:
$$gradient = \frac{\partial LOSS}{\partial w}|_{w=w_0}$$
有了梯度,也就找到了Loss下降的方向,此时我们就根据梯度下降的方向去调整w的值即可完成Loss的降低,那么调整的步长就称作learning rate(学习率),记作η:
$$w_1 = w_0 – \eta * (\frac{\partial LOSS}{\partial w}|_{w=w_0})$$
这里我们需要操心另外一个问题:局部最优和全局最优。如上图,其实“全局最优解”是在最右侧的,但是在最左侧会有一个小的“局部最优解”,如果我们的w_0在最左侧开始迭代,那么就很容易陷入局部最优。因此一个合适的初始预权重是非常重要的。
1.3 函数式的构成
前面我们一直用y = b + w_i * x来作函数的例子,但实际情境中根本不可能是这么简单的线性函数,而是各种稀奇古怪的函数,例如: