引言

　　说到“渲染”这个词，大家肯定不陌生，就算非CGer也知道渲染就是通过大量计算将三维真实画面呈现在电脑屏幕上的技术。能够提供渲染操作的平台叫做渲染器，常规情况下，渲染器和渲染操作都是基于一些图形学应用程序编程接口来实现的，例如我们熟知的opengl、directX，这些编程接口极大地方便了程序员对于图形、渲染方面的编程。但在本系列博客中，为了能更彻底地理解渲染器或游戏引擎底层的渲染原理，我们将抛开这些编程接口，仅使用C++语言，在Qt软件平台上完成一套具有渲染功能的渲染器。（基于软件平台的渲染器就简称为“软渲染器”）

　　凡事在做之前，必须先明确做它的意义是什么。这里肯定有小伙伴会问，为什么放着opengl、dx这些接口不用，非要用C++来复现底层呢？这个问题其实就好比为什么ai课上要求手写神经网络、汇编课要求汇编语言写计算器，从开发层面来讲，这样的开发一定是低效的，做出来的成品也一定是简陋的，但是它能够督促我们了解底层的原理，体会底层的设计架构，巩固基础。我选择复现软渲染器，也是因为自己对于渲染管线、光栅化、裁剪剔除等渲染器内置功能仅停留在“知道原理”的层面，而完全不知道其实现方式（计科学生的课程实在不怎么学这些）因此希望能够在阅读他人论文、博客的过程中，进一步理解渲染管线中每一步的原理，掌握每一步的实现方法，从而在图形学领域打下坚实基础。

（最后感谢yangWC大佬的博客：https://yangwc.com/categories/Soft-Renderer/，给了我非常大的启示）

光栅化简介

　　当今图形学渲染主要是两大途径，一个叫做光栅化渲染（rasterization），一个叫做光线追踪（ray-tracing）。它们的区别主要在于：在光栅化渲染模式中，物体的基本单位是三角形，我们需要把空间中的所有三角形找出来、进行坐标变换，然后通过一些数学算法来完成描线和填面操作；光线追踪的思路是让光线从眼球出发，在各个物体上进行反射，最后得到对应点的最终颜色。前者的效率较好，但渲染质量一般；后者随着反射次数的提升，渲染质量大幅度提升，代价则是效率的大幅度下降。
　　光栅化本身的原理很简单，就是拿到世界中存在的所有顶点，判断其是否被抛弃、坐标变换到哪里，最后再进行描线和填充。它的支持核心叫做渲染管线，其中实现了光栅化的全部功能，接下来对光栅化进行一个简单的介绍。

　　首先我们需要明确：什么是渲染，什么是流水线？
　　渲染，可以简单理解为：根据一个模型的各种信息（坐标、顶点属性、材质、环境作用等），将该模型输出成三维图像的过程。大家在打3D游戏的时候会看到各种各样的模型，其实在初始状态下，它们都只是一系列的数据流信息，只有经过渲染器的计算分析之后，屏幕才能将完整的模型和附加视觉效果（如光照、晕影、模糊）完整地展现出来。因此可以简单理解为：渲染就是将模型数据信息转换为图像的操作过程。
　　流水线是工业引申出来的一个名词，它指的是对工业物品进行加工的秩序。它的特点在于：每个被加工物品要经过多个环节加工； 每个环节有一个工人； 每个工人加工完当前物品立刻加工下一个物品。如此，流水线上的物品应该是one by one的（紧挨着，不会有间隙），并且每个加工者也是闲不下来的。

　　结合起来看，渲染流水线（下文我们简称RP）指的就是：符合流水线秩序要求的渲染操作。被加工的对象是模型数据中的顶点、片元/像素，加工者是我们后文会详细解释的硬件、着色器，而工作区间就是我们电脑的gpu+缓存（两者加在一起就是我们所熟知的显卡）。RP的意义：对每一个图形单元进行多轮环节的分析，从而确定它最后在屏幕上的位置、颜色等状态。
　　接下来我们将详细介绍一下渲染流水线的具体流程。

　　RP一共分为三个阶段：应用阶段（ CPU向GPU通讯）几何阶段（分析并变换图形单元）光栅化阶段（将图形单元转化为屏幕上的结果）。

①应用阶段
　　这一部分比较偏硬件，开发者一般不需要关心这一阶段的内容，不过还是打算简单讲一下CPU和GPU之间的通讯过程。
　　首先，模型等原始数据储存在计算机的硬盘当中。硬盘的好处是可以长期安全地储存数据，但是计算机并不能直接应用硬盘中的数据，所以需要将数据从硬盘加载到内存RAM中，便于与其他硬件进行沟通。然后RAM会把数据传输到显存VRAM中，再由VRAM提供数据给显卡进行分析使用。使用VRAM是因为内存无法直接访问显卡（或者说访问效率过于低下），而VRAM作为显卡的一部分，与GPU的交流更加安全快捷，因此我们需要把数据先放入VRAM进行缓冲过渡。
　　当我们的数据成功被传入到显卡中后，CPU就可以向GPU发号施令了。首先是要确定渲染状态，渲染状态指的是场景、模型网格的渲染方式，即设置加工的“设备”或者加工材料，可以理解为加工设置。 渲染状态设置完成后，CPU（无耻资本家）调用“DrawCall”指令，命令GPU（苦逼打工人）开始渲染工作。Draw Call其实就是CPU调用图形编程接口命令GPU进行渲染的一个形象描述。这里多提一嘴，DrawCall过多会严重影响效率，不过并不是因为GPU渲染不动了，而是因为CPU提交指令的效率太低，过多的DrawCall会使得CPU过载。一个好的解决办法就是让CPU在RAM中将多组命令打包传入命令缓冲区，从而完成“批处理”的思想。

②几何阶段
　　上一步我们说到，CPU发号施令让GPU开始干活了，此时GPU所拥有的只是从硬盘输送过来的一大堆顶点数据。所以我们的第一个“流水线工人”就是专门处理顶点数据的，它叫做顶点着色器（Vertex Shader），是整个渲染流水线两大最关键着色器之一。（首先必须明确一件事情：对于任意3D模型网格体的基本单位都是三角形（如下图），而每个三角形是由3个顶点确定的。所以我们说当顶点确定下来了，模型也就基本确定下来了）

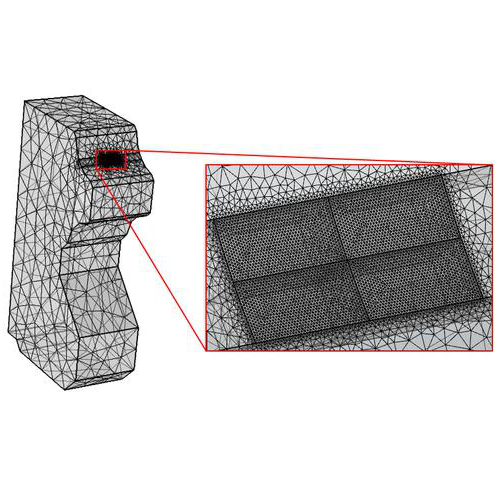
　　顶点着色器的作用是对顶点进行预处理，其中最重要的一步是进行坐标变换。顶点本身的坐标是以模型空间的锚点作为原点的，顶点着色器需要将顶点转移到我们想要的空间系中，就需要历经以下过程：模型空间->世界空间->观察空间->裁剪空间，这一步的流程可以参考下图：

　　（ps：顶点着色器暂时不会把顶点变换到屏幕空间，一般以裁剪空间作为变换结尾）
　　此外，它还可以通过光照公式，来计算每个顶点的光照颜⾊，并通过纹理坐标来映射顶点的纹理图样。有时候我们会想做一些动态效果，如蠕动、落叶、水波效果，它们本质上就是模型顶点在不断发生位移，因此也需要顶点着色器进行计算输出。
　　经过顶点着色器的变换之后，顶点位置基本就确定了，那么模型的基础形态也就确定下来了。但有时候，导入的模型质量不够高（网格精度低，贴图不精细），在视觉上看起来会非常难受，所以接下来需要引入曲面细分着色器：使用合适的细分算法，来生成高精度网格，从而提高游戏画面的细节（如下图）。比较令人舒心的是，这部分功能一般是内置的、不可编程的，所以我们无需关注怎么去改写它，只需要静待它自动处理就好了。

　　现在模型基本上已经完全确定下来了，是不是就可以把模型向屏幕空间进行映射了呢？别着急，要知道整个场景中，不是所有的物体都在我们的视野当中。为了减少无用数据的处理，提高渲染效率，我们需要将视野之外的顶点全部裁剪掉。上文我提到了，顶点着色器会将顶点变换到裁剪空间，在这个空间中管线可以迅速判断哪些点在视野当中，哪些点不在。然后便可以将视野外的顶点、模型区域全部裁剪掉，将保留下来的顶点进行屏幕映射，从而为几何阶段收尾。

③光栅化阶段
　　上文我们处理完了所有顶点，但是有一个比较大的问题是：现在只有一堆零散的点，没有把三角形面做出来。所以在光栅化阶段的开头，我们首先要进行三角形设置，即通过顶点信息确定三角形的边界。（这里会有一些特定的光栅化算法来做这件事情，不过实现方式比较唯一，所以我们也不需要关注它如何实现）当边界被确定下来了，那么三角形的面也就确定下来了。此时我们要做的就是三角形遍历，即检查每个像素属于哪个三角形中，或者反过来理解，每个三角形都包含了哪些像素。通过这一阶段，我们可以把所有三角形的全部信息给出，以便进行片元的计算。
　　那么接下来的这位“工人”，就是两大最关键着色器之二——片元着色器（Fragment Shader），亦称作像素着色器（Pixel Shader）。它的作用是通过对三角形三顶点的信息进行插值，从而得到三角形内片元的颜色。这是一个可编程的着色器，因此也可以在其中计算光照、颜色混合等等自定义事件。关于插值，就是根据每一个像素和其所在三角形三个顶点的位置关系，来计算出一个过渡很柔和的属性数值，这个数值不仅限于颜色数值，也可以是法线数值。

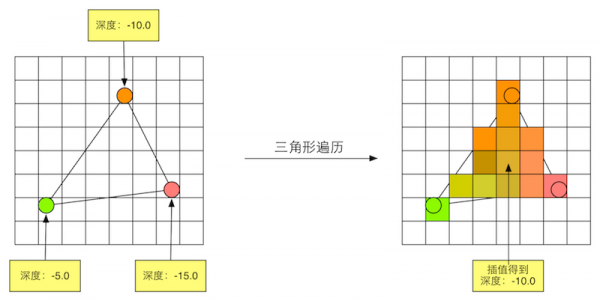
　　计算每个像素的插值结果有很多种方法，目前最主流的方法是使用“重心坐标”。因为这篇blog的重点不在这，因此就不耗费篇幅来推导了。
　　经过之前的操作，看似模型也确定下来了，三角面也确定下来了，颜色也计算过了，是不是就结束了呢？还没有，这是因为我们没有处理遮挡问题。按照常识，如果有两个点，它们在你视野中是重合的，那么你只能看到近处的，而远处的会被遮挡住。这个问题之前可没有处理过，因此我们要引入两个测试来解决它。第一个测试叫做模板测试，它可以理解为自定义的“及格线”，如果一个图元距离相机的距离过深，就会直接被剔除掉。这是一个粗筛的过程，用来把过远的、离谱的图元给丢弃；第二个测试叫做深度测试，它就是用来比较图元远近的了。当发现一个图元和缓冲区的一个图元重合，并且深度要比缓冲区图元要浅时，就在缓冲区中把原先这个图元覆盖掉。
　　当然如果涉及透明图元了，那这个问题就更加复杂了，我们在这里暂且不提。此外遮挡测试也有可能会被放在片元着色器之前进行，提前将无效的片元剔除，这样可以减轻片元着色器的工作负担。
　　至此，渲染管线的基本流程就结束了。实际上RP做的事情远比本文描述的要复杂，也会有流程上的一些出入。但是大部分引擎和渲染器都基于本文描述的原理，因此这部分的内容还是建议细看一下的。

　　在制作软渲染器之前，我们还需要明确一件事情：渲染器需要有什么功能？很显然，渲染器的功能就是输入我们的图元、模型数据，通过渲染循环附件来每帧调用渲染管线，进行输入顶点的位置变换、颜色分析等操作，最后将所有通过深度测试的顶点和片元渲染在我们的视口——画布（canvas）上。（初学者可能觉得这句话的生词太多了，没关系，在接下来的几篇blog中我会详细给大家解释）这是一个很庞大的软件体系，其中包括许多不同功能的附件，因此我们不可能把所有代码都写在一个C++文件中，而是分为多种类、多种对象进行设计。在本篇blog中，就先带大家复习（或者预习）一下C++的一些基础知识。
（接下来的内容，C++基础比较扎实的同学可以跳过了）

c++基础——类与继承

　　C++可以简单理解为具有面向对象范式的C语言，它的特点就是可以定义“类”这种能够封装大量数据的结构。我们在.h头文件中定义一下类，模板大概长这个样子：

　　它只交代了这个类里面有哪些成员，具体构造函数、析构函数、成员函数的内容都是什么，我们可以放到.cpp中进行详细解释：

　　继承是一个很重要的概念，指的是继承者类默认拥有被继承类的所有成员。被继承者类我们称作基类或父类，继承者类我们称作派生类。当然派生类可以自由地改变继承的成员，也可以给自己增添新成员。它的好处是，我们不需要在派生类中再把所有的成员定义一遍，而且当基类的成员改变时，所有的派生类都可以跟着改变，免去手动改派生类的麻烦。

c++基础——初始化列表

　　初始化列表是类调用构造函数时，比构造函数体更早执行的初始化操作，这种初始化方法更加安全：

c++基础——重载运算符

　　我们知道对于int、float等数字类型的变量，默认可以使用+-*/这些符号进行数学计算，但是像向量、矩阵这样自定义的类是无法直接使用这些符号的，因此我们需要手动定义一下这些符号在类当中的使用方法：

　　需要注意的是，传入的变量最好是const+引用类型，以保证变量安全。

c++基础——抽象类-虚函数-重写

　　这部分应该是最难理解的了。我们有时候会发现，某些基类并不具备实际含义，它只是单纯给派生类提供一个模板。例如shape类派生出三角形类、四边形类、五边形类，shape类本身没有任何实例化的意义，它只是声明一些必要的成员供给派生类来修改。那么这种类我们管它叫抽象类，而它提供的模板函数称作虚函数。具体的写法就是在成员函数前面加一个virtual，在函数头的末尾处加一个=0，表示这个函数在该类中没有任何内容，只是一个模板。而派生类对虚函数进行重新定义的操作，我们称作重写（override）。

　　需要注意的是，抽象类的析构函数也需要加上virtual标志。

c++基础——多态

　　那么接下来再来谈谈多态。多态这个特性不太好描述，举个例子：shape类派生出三角形、四边形、五边形类，并且将它们实例化。我定义三个shape类型的指针，赋值的时候分别赋值三角形、四边形、五边形实例的地址，这个时候调用三个指针的虚函数，结果是分别调用了三角形、四边形、五边形重写后的函数。这个就是多态，它体现在：同样是shape类型的指针，赋值不同的实例类型，就可以调用对应实例类型的虚函数。它的好处体现在我们不需要在一开始就给指针确定好类型，而是简单地全部定义为shape类型，这样便简化了我们的工作量。

　　那么C++的介绍部分就到此为止了，不熟悉的同学可以去网上找更多的资料，理解起来不是非常困难。接下来，我们将使用C++构建自己所需要的数学库。

数学库——二维向量

　　二维向量是最简单的向量，由两个浮点数x和y组成。二维向量在项目中的使用频率不高，但是在转换视口空间、uv映射的时候仍然会用到，因此我们仍需要构建它的类。
　　二维向量的变量成员非常简单，就是float类型的x和y；函数成员略微复杂一点，首先我们关注一下构造函数，构造函数是用来对类进行初始化的基础函数，当然也支持函数重载（overload），即不同的传入参数，构造函数有不同的初始化方法。我们常见的初始化方法有：默认构造（没有传入参数），传参构造（传入x和y），拷贝构造（传入一个二维向量）。析构函数一般没什么内容可写，直接摆在上面就可以了：

　　这里推荐大家也使用初始化列表来进行初始化。要注意的是，拷贝构造函数的传入向量前面必须要加const，网上给出的理由只是说这样更安全，但事实上不加const的话，后面有些函数写出来会报意想不到的错误。
　　接下来说说get()（获取成员变量）和set()（改变成员变量）的事。假如你的x和y是public类型的，那这两个函数没什么意义；如果是private类型的，就需要在向量类中设计public类型的set()和get()函数，以便其他对象获取或改变x和y。这个部分因人而异，不多赘述。
　　然后我们关注一下与向量性质有关的函数，一个是获取模长（magnitude），一个是单位化（normalize），都是十分简单的操作。只不过单位化我们可以做两个函数，一个是直接将向量自身单位化，一个是返还一个经过单位化的向量。

　　最后便是重载运算符了。我们打算重载+-*/，以及+=、-=、向量前面只有一个负号的情况。因为这部分代码量比较大，所以就不单放了，我直接把二维向量的全部代码粘上来：
.h部分：

.cpp部分：

数学库——三维向量

　　三维向量就比二维向量多了一个参数成员z，只需要把Vector2的部分复制过来，然后在各个函数里补上参数z就可以了。除此之外，三维向量要比二维向量多两种操作：点乘和叉乘。点乘的运算规律是：(a,b,c)·(x,y,z)=a*x+b*y+c*z，得到的值是一个没有方向的标量，而叉乘的运算规律是(a,b,c)×(x,y,z)=(bz-cy,cx-az,ay-bx)，得到的结果是一个与两向量都垂直的向量。话不多说，直接放代码：

.h部分：

.cpp部分：

数学库——四维向量

　　四维向量又比三维向量多了一个参量，只不过四维向量不存在叉乘操作，因此product函数可以删去。这部分没什么难点，直接给出所有代码：
.h部分：

.cpp部分：

　　向量部分就到此结束了。向量是大家初中就接触过的概念，比较好理解，也没有什么复杂的运算。接下来，就是一个比较磨人的数学结构了：矩阵。

数学库——矩阵

　　矩阵相比向量，难度明显上升了一些，倒不是矩阵的结构有多复杂，而是因为它有数不清的性质和抽象的概念要理解。当然，让我在这里给萌新从零讲述矩阵也不现实，因此还是建议大家对矩阵具备一定了解以后再继续写这部分代码。
　　首先要确定的事情是：我们的矩阵应该是几乘几的？在后面的项目中，我们可能会用到各种各样的矩阵，像2×2的、2×3的、3×3的等等，但我们没有必要把所有的矩阵情况都做出来。我们只需要做一个m×n的矩阵，其中m是所有矩阵中的最大行数，n是所有矩阵中的最大列数，这样所有类型的矩阵都能通过这个m×n的矩阵来表示了。那紧接着的问题是：m和n应该取多大？换句话说，我们项目中可能涉及到的最大矩阵是多大？那这部分就需要一点简单的cg知识了。
　　我们的世界是三维的，因此我们做的渲染器最高也是三维，那么理论上来讲我们对三维向量进行变换，只需要一个3×3的矩阵就足够了。但是事实上并非如此，举一个反例：如果我要对点(a,b,c)平移(x,y,z)，会发现3×3的矩阵无法将(a,b,c)变换为(a+x,b+y,c+z)，意思就是3×3的矩阵不够充分。这个时候我们需要把3×3的变换矩阵扩充到齐次空间，变为4×4的矩阵，而向量也要从三维向量扩展到四维向量（多出来的参数w默认置为1），此时我们可以推导出4×4的平移矩阵长这个样子： 

$$\begin{vmatrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \\ \end{vmatrix}$$

　　上述的矩阵就是朴素的平移矩阵，它说明了：即使是三维空间，变换矩阵的维度也至少是4——所以我们所涉及到的最大矩阵就是4×4的矩阵。矩阵类的基础成员和构造函数如下：

　　初始化16个成员变量有点麻烦。。。下面set函数的意思是将矩阵的第x行第y列的元素大小替换为e，不多赘述。
　　接下来的内容是重载运算符，矩阵的+-操作比较简单，直接对应元素加减就可以了。乘法操作主要有三种：矩阵乘数，矩阵乘向量，矩阵乘矩阵。乘数就不说了，乘向量和乘矩阵都秉承下面这个计算公式：

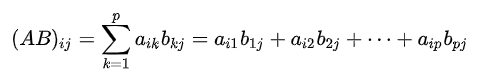
　　代码准备最后再放，我们接下来看一下各种变换矩阵：平移矩阵、放缩矩阵、旋转矩阵、透视投影矩阵、正交投影矩阵、lookat矩阵、屏幕变换矩阵。这里我们重点关注一下前三个矩阵，它们比较基础。后四个矩阵在2维渲染中暂时用不上，并且推导过于复杂，再加上本篇篇幅过长，因此先选择性跳过了。
　　平移矩阵、放缩矩阵和旋转矩阵的推导我写在了笔记本上（因为html不好编辑公式和图像），如下：

　　旋转操作只推导了按照x、y、z轴进行旋转的变换矩阵，按照任意轴旋转的矩阵我会放到四元数的博客里讲。
　　那么我们基础的4×4矩阵就已经构造完毕了，接下来是全部源码。
.h部分：

.cpp部分：

　　至此我们线性代数部分就结束了（其实没有完全结束，有些复杂矩阵的推导和编写需要放在后面的文章讲述）。
　　下一篇文章会讲述渲染器的核心部分——管线篇。