本篇从采样的数学角度来解析：如何采样才能更好的估计渲染方程中的积分部分，从而提升光线追踪结果的正确性。

Part1 均匀采样的蒙特卡洛积分

　　现在我们的渲染仍然存在一个问题：噪声太多，尤其是黑色噪点，这是因为我们使用的是均匀采样的蒙特卡洛积分，这种采样方式是有很大缺陷的。当然可能你还不知道蒙特卡洛积分到底是个啥，先不着急，我们首先回顾下我们的渲染方程：

$$L(x→out)=L_e(x→out)+\int_\omega^\omega f_r(x,in→out)L(x←in)cos(\pmb N,\pmb {in})d\omega$$

　　对于镜面反射而言，每根出射光线只对应一根入射光线，因此积分操作相当简单，不多赘述；然而对于漫反射，各个方向来的入射光线都会对同一根出射光线有贡献，即每根出射光线需要由很多入射光线积分得到。如果要精确计算出结果，则需对入射到该点的半球面上的所有光线做积分运算。然而直接求解该方程的精确积分值非常困难，在实际光线追踪应用中我们只能通过采样少量的光线来拟合这个积分的近似解，这便是蒙特卡洛积分的思路。回顾一下我们之前的程序，会发现漫反射材质的反射方向是均匀随机的，因此我们的程序本质上使用的是均匀采样的蒙特卡洛积分。

　　接下来我们解析一下均匀采样的蒙特卡洛积分的计算过程。假设我们有一个复杂函数f(x)，现在要求它在(a,b)区间上的近似解，那么我们可以直接在(a,b)区间上均匀采样，采到x1的时候，我们估算积分面积为底（b-a）乘上高（f(x1)），这就是我们第一次采样得到的面积。第二次我们采x2，那么面积就变成了(b-a)*f(x2)，如此反复采样下去，最后计算一个均值就是估算的积分值了。如下图：

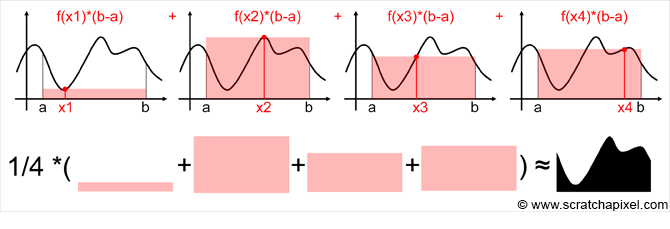
　　那么我们不难总结出来，在均匀采样的前提下，蒙特卡洛积分的表达式为：

$$S=\Sigma_{k=1}^N(f(x)*(b-a))*\frac{1}{N}。$$

　　事实上，我们之前的程序就是这样采样的：当光线击中一个漫反射材质后，它会均匀地随机向某一个方向发出反射（即均匀采样），最后我们把多个方向的采样结果取了均值，得到最后的结果。

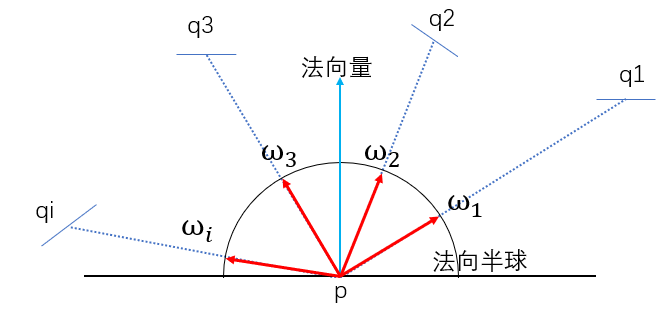
　　但是从渲染结果上大量的噪点可以推断出，均匀采样并不是合适的采样选择，接下来我们来讨论一下为什么均匀采样会导致严重的噪点现象，而合适的非均匀采样可以更好的拟合渲染方程的积分。

Part2 非均匀采样/重要性采样的意义

　　我们知道，在积分过程中需要采样大量的光线样本才能让积分收敛接近真实值，有两种情况会直接导致积分结果严重偏离真实值（即出现噪点）。一、采样数不足。如果只有零星的几次采样，很有可能它们都没有追踪到光源，最后只留下了黑色印记；二、入射光线样本与真实光线的分布有偏差，它指的是对于均匀随机采样的反射光线，可能大部分会落到没有意义的黑暗表面，只有少部分能够追踪到更有意义、对颜色贡献更大的光源上，这样大部分的光线其实是没有作用即浪费掉了。那么，如果能让采样的光线样本有较大的概率偏向较亮的方向，而不是像前面提到的均匀采样，这样就可以减少无意义的追踪，这就是重要性采样。

　　换个说法，光源和非光源对于着色的贡献是不同的。场景中如果少了一堵墙，它对于附近物体的颜色影响会小；但是场景中如果少了一盏灯，它对于附近物体的颜色影响就会很大。对于这个影响、贡献很大的光源，我们必须保证在随机采样的时候能够射中它。一旦没有射中，那么就会与预期结果产生较大差异（结果就是别的地方都亮了 到你这突然黑了一块）

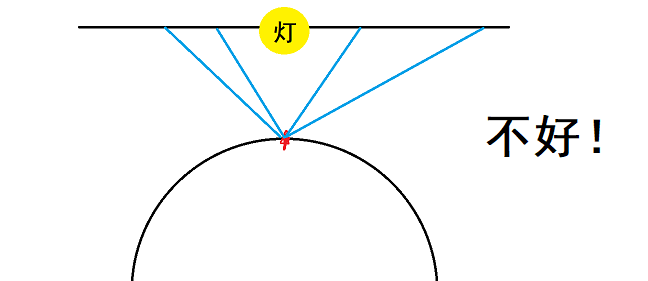
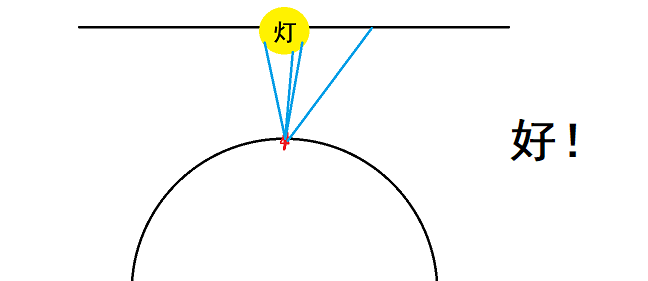
　　 因此，我们必须摒弃均匀采样的理念，提高向较亮方向采样的概率（注意不一定是光源，也可能是间接光更亮的地方），这就体现了我们非均匀重要性采样的主题。要注意的是，这一切还只是“理论猜测”，接下来我们将从数学角度来证明：提高光源方向采样的概率在数理统计中确实能够提高渲染方程蒙特卡洛积分的估计精度（降低方差）。首先，我们先来看看非均匀采样的蒙特卡洛积分公式。

Part3 非均匀采样的蒙特卡洛积分

　　首先回忆一下均匀采样估算积分的公式：

$$S=\Sigma_{k=1}^N(f(x)*(b-a))*\frac{1}{N}$$

　　均匀采样的概率密度函数PDF其实就是定值1/(b-a)。对于非均匀分布，假设其采样的概率密度函数PDF为非定值函数p(x)，那么估算积分的结果就是：

$$S=\Sigma_{k=1}^N\frac{f(x)}{p(x)}*\frac{1}{N}$$

　　这个式子可没有均匀采样公式那样好理解，所以我们直接证明一下这个式子的期望确实是f(x)在(a,b)区间上的积分就好了：对于任意函数g(x)，若x的概率密度为p(x)，其期望为：

$$E(g(x))=\int_a^b g(x)p(x)dx$$

　　假设g(x)=f(x)/p(x)，p(x)就是x的概率密度，那么有：

$$E(g(x))=E(\frac{f(x)}{p(x)})=\int_a^b \frac{f(x)}{p(x)}*p(x)dx=\int_a^b f(x)dx$$

$$h(x)=\Sigma_{k=1}^N\frac{f(x)}{p(x)}*\frac{1}{N}=\Sigma_{k=1}^N g(x)*\frac{1}{N}$$

$$E(h(x))=E(\Sigma_{k=1}^N g(x)*\frac{1}{N})= \Sigma_{k=1}^N \frac{1}{N}*E(g(x))=\int_a^b f(x)dx$$

　　可以看到，h(x)函数“多次采样f(x)/p(x)的值作平均”的期望恰好是f(x)在(a,b)区间上的积分。因此，我们把“多次采样f(x)/p(x)取均值”的式子作为非均匀蒙特卡洛的无偏估计，也就是我们刚刚提到的那个式子：

$$S=h(x)=\Sigma_{k=1}^N\frac{f(x)}{p(x)}*\frac{1}{N}$$

　　也就是说，如果我们给定一个非均匀采样的PDF并按照这个PDF来采样，那么每次我们把采样结果f(x)除以一下它的PDF值，最后再相加做平均，这样就能无偏估计蒙特卡洛积分的结果了。

Part4 选取PDF函数降低方差

　　上面我们得到了非均匀采样估计蒙特卡洛积分的公式。尽管我们做到了无偏估计，但是问题在于：选择不同的p(x) （即PDF函数） 会导致不同程度的方差。因此现在的问题就是：p(x)函数到底怎么选，才能将方差降到最低，从而更精确地估计积分值？话不多说，我们继续从方差的角度来作推导：

$$\sigma^2(h(x))=\sigma^2(\Sigma_{k=1}^N g(x)*\frac{1}{N})=\Sigma_{k=1}^N \frac{1}{N^2} \sigma^2(g(x))$$

$$=\frac{1}{N^2}\sigma^2(N*g(x))=\frac{1}{N}\sigma^2(g(x))$$

　　这其实说明了两件事：一、增大采样数N确实可以降低方差，这对应了前面说的采样数的问题；二、也是我们最关注的一件事，蒙特卡洛积分公式的方差与g(x)（即f(x)/p(x)）的方差是成正比的。因此，要想让蒙卡积分采样的方差最小，就要让f(x)/p(x)采样的方差尽可能最小。根据概率论的知识我们知道，当一个函数是定值函数时，其采样的方差可以降低到0（就是无论你采样的x是几，最后得到的值都是相同的，这样方差就是0了）。因此要想让g(x)采样的方差降到0，就要让f(x)/p(x)是定值。这样我们就得到了结论：当f(x)/p(x)是定值，即p(x)和f(x)走势完全相同，可以写成p(x)=k*f(x)的形式时，蒙特卡洛积分的方差是最小的。

　　拿f(x)=x^2、范围0~1这个函数来举例，根据上述规则，为了让方差最低，PDF函数的形式应当为k*x^2，由于概率密度函数的积分必须为1，这样就能解出k的值：

$$p(x)=k*x^2$$

$$\int_0^1 p(x)dx=1$$

　　解出来k=3，因此我们选择的PDF函数为p(x)=3*x^2。当然这只是函数比较简单的情况下，在大部分情况下被积函数f(x)都是极其复杂的，其反导会很难解甚至不可解，这样即使我们令p(x)=k*f(x)也没办法解出k的值来。所以很多时候我们只是找一个走势大致相同的简单p(x)，尽可能地将方差降到最低。例如对于一个陡缓不规则的单调递增函数f(x)，我们可以简单粗暴地让p(x)=x，这样走势与f(x)大体相符，也能保证方差比均匀采样低很多。

　　说到这里，我们就可以证明“提高光源方向采样的概率能够提高渲染方程蒙特卡洛积分的精度”了。拿出我们的渲染方程：

$$L(x→out)=L_e(x→out)+\int_\omega^\omega f_r(x,in→out)L(x←in)cos(\pmb N,\pmb {in})d\omega$$

　　被积部分可以写作f(x)函数：

$$f(x)=f_r(x,in→out)L(x←in)cos(\pmb N,\pmb {in})$$

　　我们知道如果一个光线来自于较亮的区域，那么它的L(x←in)会非常大，f(x)也会相应更大，根据前面的结论，当采样这个方向的PDF值（即概率密度）也随之更大时，f(x)与PDF走势更接近，蒙特卡洛积分便会有更精准的解（准确说是方差最小、最不容易出噪点的解）。这样就从数学角度证明了：指向光源的方向，应该有更大的采样概率，才能更好的降低渲染方程拟合的方差，减少噪点。

Part5 随机采样数生成

　　根据前面的结论，我们能快速找到合适的PDF函数。但是在编程语言中，我们实现随机数的方法大部分是均匀随机的，如何通过均匀随机数来完成非均匀概率密度的采样呢？这里有几个方法。

一、逆采样法

　　我们计算机只能生成服从U~U(0,1)分布（即均匀分布）的随机数，然而我们的X服从的是不均匀的分布，因此我们要想办法找到一个变换T，能让T(U)和X做到同分布，这样我们就能利用计算机生成的U分布来生成X的分布了。这个T是这样子的：

$$T(U)=F_X ^{-1} (U)$$

　　能证明T(U)与X是同分布的。其证明过程如下：

$$P(F_X ^{-1} (U) \leqslant x) = P(inf[t : F_X (t) = U] \leqslant x) = P(U \leqslant F_X (x)) = F_U(F_X (x)) = F_X (x)$$

　　既然T(U)与X是同分布的，那么过程就是这样的：对于给定的一个PDF，首先通过积分求出它的CDF（概率累积分布函数）：

$$y=CDF(x)=\int_{-\infty} ^x PDF(x)dx$$

　　然后取其逆函数：

$$x=\int_{-\infty} ^y PDF(y)dy$$

　　这个y就是前面提到的F^{-1} (X)。因此当我们产生服从U~U(0,1)分布的随机数u时，代入到y这个式子得到的结果和目标X的概率分布是一样的。举个最简单的例子：

$$f(x)=x^2,x\in (0,1)$$

$$PDF(x)=3*x^2$$

$$CDF(x)=\int_0^x 3*t^2dt$$

$$CDF(x)=[t^3]_0 ^x=x^3$$

$$y=CDF^{-1}=\sqrt[3] x$$

　　这种方法有一个明显的缺陷：如果CDF函数没有逆函数的解析解，那么这个方法就没法继续用了。因此我们还有第二种方法：拒绝采样。

二、拒绝采样法

　　这种方法相比于逆采样法会直观很多，一张图就能说明它的原理：

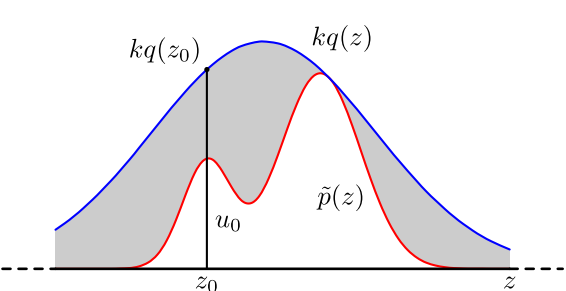
　　对于一个PDF函数，我们可以构造一个程序可抽样的分布q(x)，如均匀分布或高斯分布，要求它能够完全把PDF函数包含进去，所以我们可以给它乘一个k变成kq(x)。然后我们先根据kq(x)来生成样本z0（意思就是生成的样本都会在kq(x)函数的内部）我们接受它的概率就是p(z0) / kq(z0)。那么我们只需要再从U~U(0,1)的分布中随机一个u出来，如果u<p(z0) / kq(z0)，那么接受这个采样值就好了。

　　当然还存在更多厉害的生成采样数的算法，如马尔科夫蒙特卡洛采样、Gibbs采样等，不过不是我们这里讨论的重点，因此就不再赘述了。

Part6 渲染实战中的PDF选择

　　现在我们的数学理论基础已经非常完备了，那么就需要转向实战环节——在光线追踪程序中实现重要性采样。那么依然回到我们的渲染方程上：

$$L(x→out)=L_e(x→out)+\int_\omega^\omega f_r(x,in→out)L(x←in)cos(\pmb N,\pmb {in})d\omega$$

　　我们把积分部分提出来：

$$f()=f_r(x,in→out)L(x←in)cos(\pmb N,\pmb {in})$$

　　这个被积函数显然可以分为三部分：L，即入射光线本身的强度；cos值，即入射反向光线与法线的夹角余弦值；f_r，即材质的BRDF。我们将对这几项分别进行重要性采样的分析。

一、cosine的重要性采样

　　cos项作被积函数，PDF为了拟合其走势，可以设计成c*cos的形式：

$$\int_{\Sigma^+}c*cos\theta_id\omega=1$$

$$c=\frac{1}{\pi}$$

　　但是注意到积分里的dw是个高维立体角，现在需要将它拆成方向角ϕ和天顶角θ，从而得到一个关于方向角和天顶角的PDF：

$$d\omega=sin\theta d\theta d\phi$$

$$\int_{\Sigma^+}\frac{cos\theta_i sin\theta}{\pi} d\theta d\phi=1$$

$$pdf(\theta,\phi)=\frac{cos\theta sin\theta}{\pi}$$

　　PDF的自变量有两个量，我们可以根据边缘概率公式和条件概率公式将两个量分开，然后使用逆采样法，分别求两个量的cdf函数和cdf逆采样函数（由计算机生成的均匀随机数用U1和U2来表示）：

$$pdf(\theta)=\int_0^{2\pi}pdf(\theta,\phi)d\phi=sin2\theta$$

$$cdf(\theta)=\int_0^\theta sin2tdt=1-cos^2\theta$$

$$逆采样：cdf^{-1}=\theta=arccos(\sqrt{1-U_1})$$

$$pdf(\phi | \theta)=\frac{pdf(\theta,\phi)}{pdf(\theta)}=\frac{1}{2\pi}$$

$$cdf(\phi | \theta)=\int_0^\phi \frac{1}{2\pi}dt=\frac{\phi}{2\pi}$$

$$逆采样：cdf^{-1}=\phi=2\pi U_2$$

　　现在我们已经获得了方向角和天顶角的采样方式了，我们还需要把它转换成向量的x、y、z形式，则有：

$$x=sin\theta cos\phi=cos(2\pi U_2)\sqrt{U_1}$$

$$y=sin\theta sin\phi=sin(2\pi U_2)\sqrt{U_1}$$

$$z=cos\theta=\sqrt{1-U_1}$$

　　推导就结束了。那么我们在程序里要怎么做呢？首先我们要生成两个符合U~U(0,1)均匀分布的随机数U1和U2，然后将两个随机数代入上述的式子中，就得到了采样的弹射光线(x,y,z)，注意此时需要把这个弹射光线转换到对应的空间，因为我们得到的(x,y,z)只是法线竖直向上情况下的向量，如果法线指向其他方向，就必须把弹射光线变换到对应的空间。已知原空间的方向向量V，以及现空间的法线N，那么有：

$$helper=(1,0,0) || helper=(0,1,0)$$

$$tangent=N×helper 并归一化$$

$$bitangent=N×tangent 并归一化$$

$$V’=V.x*tangent+V.z*bitangent+V.y*N$$

　　这个算法能够把原空间的方向向量转换到对应法线的空间的方向向量V’，这个转换在光线追踪渲染器终结版那篇blog也用到了。

　　得到的光线强度别忘了除以pdf，这里要注意pdf应该取pdf(w)而不是pdf(θ,φ)，因为两者的度量是不同的。其优化效果如图所示：

二、BRDF的重要性采样

　　这里存在一个很大问题，就是博客至今还没有讲过Disney、cook-torrance和ggx的BRDF微表面模型。所以对微表面模型不熟悉的小伙伴可以先跳过这一节，当然如果你已经熟悉以上模型了，可以继续看这部分内容。

　　这里我们拿cook-torrance模型来举例，分析一下BRDF如何实现重要性采样。cook-torrance这个模型我在brdf的博客中有提到，还整了个活把它的brdf给拆了出来：

$$f_r=\frac{(\frac{|\frac{\eta_2cos\theta_1-\eta_1cos\theta_2}{\eta_2cos\theta_1+\eta_1cos\theta_2}|^2+|\frac{\eta_1cos\theta_1-\eta_2cos\theta_2}{\eta_1cos\theta_1+\eta_2cos\theta_2}|^2}{2})(\frac{1}{m^2cos^4\theta_h}e^{-(\frac{tan\theta_h}{m})^2})(min[1,\frac{2(\pmb N·\pmb H)(\pmb N·\pmb {out})}{\pmb{out}·\pmb H},\frac{2(\pmb N·\pmb H)(\pmb N·\pmb {in})}{\pmb{out}·\pmb H}])}{\pi(\pmb N·\pmb {in})(\pmb N·\pmb {out})}+k_d$$

　　好吧不闹了，它的原式是长这样的：

$$f_r=\frac{F(\beta)D(\theta_h)G}{\pi(\pmb N·\pmb {in})(\pmb N·\pmb {out})}+k_d$$

　　F指的是菲涅尔方程，D指的是为平面分布函数，G指的是几何阴影项：

$$F_p=\frac{\eta_2cos\theta_1-\eta_1cos\theta_2}{\eta_2cos\theta_1+\eta_1cos\theta_2}（偏振光p方向）$$

$$F_s=\frac{\eta_1cos\theta_1-\eta_2cos\theta_2}{\eta_1cos\theta_1+\eta_2cos\theta_2}（偏振光s方向）$$

$$F=\frac{|F_p|^2+|F_s|^2}{2}（非偏振光）$$

$$D(\theta_h)=\frac{1}{m^2cos^4\theta_h}e^{-(\frac{tan\theta_h}{m})^2}$$

$$G=min[1,\frac{2(\pmb N·\pmb H)(\pmb N·\pmb {out})}{\pmb{out}·\pmb H},\frac{2(\pmb N·\pmb H)(\pmb N·\pmb {in})}{\pmb{out}·\pmb H}]$$

　　brdf公式粗略地分成了漫反射部分和镜面反射部分。对于漫反射部分可以与前面提到的cosine重要性采样结合在一起，就是pdf=cosθ/π。

　　再来看镜面反射部分，无非就是拆成D、F、G三项。对于菲涅尔项F需要知道采样方向后才能计算，所以无法计算它的pdf；对于几何阴影项G并不连续，也无法计算它的pdf。因此只剩下一个平面分布函数D可以计算了，我们希望找到一个正比于D项的pdf函数。

　　回忆D项的物理意义：每单位面积，每单位立体角所有法向为wh的微平面的面积。其公式为：

$$\int_H^2 cos\theta_hD(\omega_h)d\omega_h=1$$

　　好巧不巧，它的形式恰好是对某个式子的积分结果为1，那么用它来做pdf再合适不过了。但是wh我们没法直接用，所以需要把wh带换成wi的形式：

$$\frac{d\omega_h}{d\omega_i}=\frac{1}{4(\omega_h·\omega_i)}$$

$$pdf(\omega_i)=\frac{cos\theta_h}{4(\omega_h·\omega_i)}D(\omega_h)$$

　　这样我们就得到了平面分布函数的pdf函数了。采样的时候，我们可以不对wi直接采样，而是直接根据wh直接采样微平面法线，再将wo转换为wi，经过一段复杂的推导（原谅我犯懒了），就能得到方向角和天顶角的采样公式：

$$\theta_h=arctan\sqrt{-m^2*ln(1-U1)}$$

$$\phi_h=2\pi U2$$

　　 然后转化为(x,y,z)向量即可，方法与cosine重要性采样那里提到的方法相同。

三、L的重要性采样

　　回想我们的PART-2，其实一直在说的就是这件事：有时候场景中的光源非常小，导致大部分追踪的光线都打在了黑暗的地方从而浪费掉了，因此我们要增大对于光源的追踪概率PDF。

　　这里我们使用一个非常激进的思想：我们把光照分为直接光照和间接光照。对于直接光照的部分，我们直接全部对光源径直采样！让弹射光线都直接找光源！这件事听着很不靠谱，但是在cornell box这样的场景中，这个方法几乎无懈可击。假设场景中有个面片光源，其面积为A，那么我们采样就对这个灯光面片进行均匀采样，即pdf=1/A。回顾我们之前讲渲染方程的博客，曾经提出一个适用于光源面片的渲染方程区域公式：

$$L(x→out)=L_e(x→out)+\int_A^A f_r(x,in→out)L(y→-in)V(x,y)cos(\pmb N,\pmb {in})cos(\pmb {N_y},-\pmb {in})\frac{dA_y}{r_{xy}^2}$$

　　这个式子还是不好用，因此我们可以根据下图的原理来变换一下：

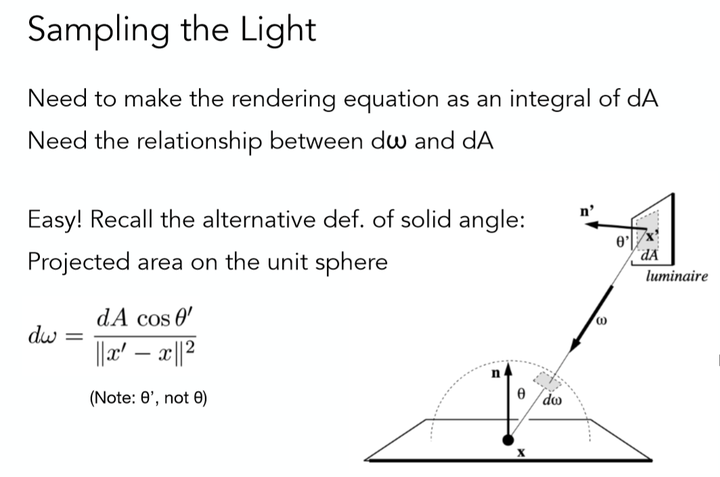
　　从而得到了一个新的渲染方程形式,其中x是着色点，x’是光源采样点：

$$L(x → out)=L_e(x→out)+\int_A^A f_r(x,in→out)L(y→-in)\frac{cos\theta cos\theta’}{||x’-x||^2}dA$$

　　那么我们便可以把光照分为两部分：1、直接光照，直接对光源采样，pdf是1/A；间接光照，就是类似漫反射采样，pdf使用cosine或者brdf的重要性采样pdf。这里还有一个小问题，就是直接对光源采样的话，你不能保证着色点和采样点之间没有遮挡。因此这里就需要稍微求个交，检查着色点发射的射线到底能不能直接打到光源上。如果被阻挡，那么此方向就不能作为直接光源的采样点了。上一份官方的伪代码：

四、多重重要性采样

　　这里前面我们介绍了对cosine重要性采样和对BRDF重要性采样，那么我们到底用哪个比较好呢？如果我们直接对光源进行采样，也就是使用L的重要性采样，效果如图：

　　可以看到，下方粗糙板子的反射效果比较好，但是上方光滑板子的反射效果就很差，这是因为它的brdf只有一个小范围对计算结果有贡献，而光源比较大，那么对大光源进行均匀采样的时候，很难恰好找到有贡献的范围，因此就会出现零零星星光点的现象。

　　如果我们使用brdf重要性采样，结果会是这样的：

　　可以看到光滑板子的反射效果比较好，但是粗糙板子的反射效果就很差，这个原因比较只管，就是粗糙面板的反射方向很随机，很难保证它能正好命中光源。如果击中不了光源，就会导致该有反射的地方完全没有亮度。

　　因此我们看到光源重要性采样和材质重要性采样各有各的长处，如果能够把它们有机地结合在一起，就能处理绝大部分有噪声的情况了。假设有n种采样分布，每种采样ni次，那么i,j就代表第i种采样的第j个采样点。其结合的公式为：

$$F=\Sigma_{i=1}^n \frac{1}{n_i} \Sigma_{j=1}^{n_i}\omega_i(X_{i,j})\frac{f(X_{i,j})}{p_i(X_{i,j})}$$

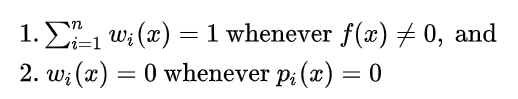
　　下面证明其无偏性：

$$E(F)=\Sigma_{i=1}^n \frac{1}{n_i} \Sigma_{j=1}^{n_i} \int_\Omega \frac{\omega_i(x)f(x)}{p_i(x)}p_i(x)dx$$

$$=\int_\Omega \Sigma_{i=1}^n \omega_i(x)f(x)dx=\int_\Omega f(x)dx$$

　　那么最后一件事就是，如何分配权重w？其实这就像我们平时组队做作业打比赛一样，谁擅长啥就去做啥。对于粗糙材质，直接光源采样就要发挥最大权重；对于光滑材质，BRDF重要性采样就要发挥最大权重。效果如下：

　　 这样就将各个重要性采样有机地结合在了一起，从而在光滑表面、粗糙表面都有比较优秀的反射效果。