一、渲染管线概述

管线一共可以分为3大概念阶段：应用阶段、几何阶段、光栅化阶段。

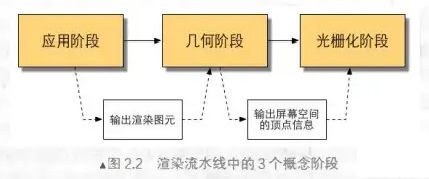
应用阶段：主要是准备好各种场景数据：例如相机位置、视锥体、场景里的模型、纹理光源等，简单做一些粗粒度剔除（剔除太远看不到的物体），最终输出渲染图元(例如点、线、三角面)，传递给几何阶段

几何阶段：几何阶段的一个重要任务是：使用空间变换 将顶点变换到屏幕空间，并传递打包每个顶点对应的深度值、着色、法线等相关信息，交给光栅化阶段

光栅化阶段：使用几何阶段传递来的数据在屏幕上产生像素，决定每个渲染图元的哪些像素应该被绘制到屏幕上。它需要对几何阶段得到的逐顶点数据（纹理坐标、顶点颜色……)进行插值，然后进行逐像素处理并渲染出最终图像

每个阶段的各个模块功能详见C++光栅化软渲染器（上）框架篇 – PULUO

整个硬件之间的协作流程如下图：

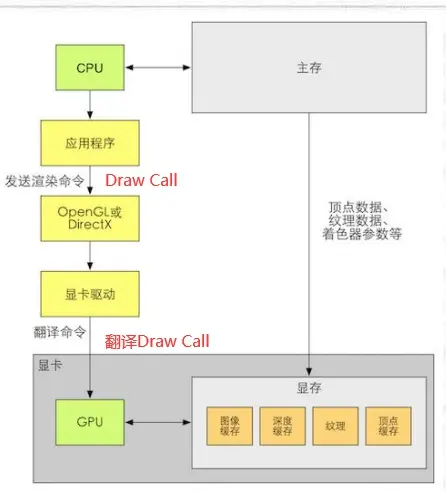
所谓DrawCall，就是CPU调用图像编程接口，以命令GPU进行渲染工作。计算机维护了一个命令队列，CPU不断往里面添加渲染命令，然后GPU接到队列中的命令后逐个执行。

CPU的DrawCall是非常耗时的，DrawCall越碎越多，最终的效率就越低。因此可以使用合批处理：把很多小的DrawCall合并成一个大的Draw Call。

需要注意的是，由于我们需要在CPU的内存中合并网格，而合并的过程是需要消耗时间的。因此，合批更加适合于那些静态的物体，例如不会移动的大地、石头等，对于这些静态物体我们只需要合并一次即可。当然，我们也可以对动态物体进行批处理。但是，由于这些物体是不断运动的，因此每一帧都需要重新进行合并然后再发送给GPU,这对空间和时间都会造成一定的影响。

二、空间变换与矩阵

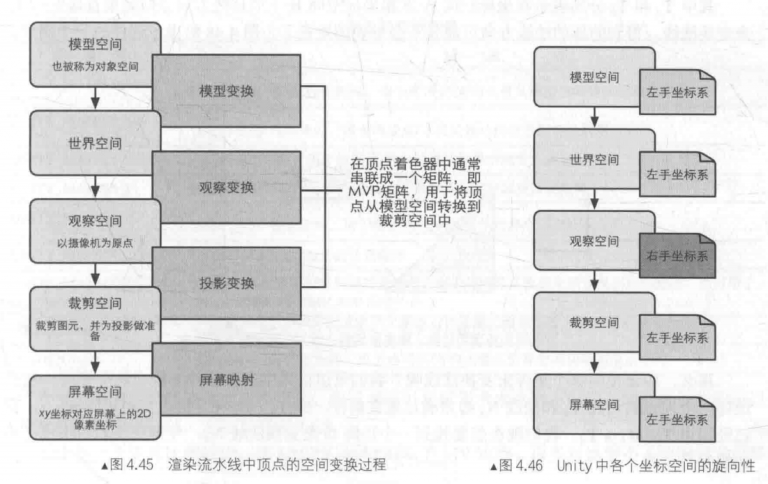
介绍方面的话就不多说了，直接进入主题。先复习一下渲染管线中，一个顶点是如何从模型空间的坐标计算出最终在屏幕上的坐标的：

像模型变换和观察变换，本质都是对顶点进行缩放、旋转、平移等操作完成的。因此首先要了解一下最基础的平移、旋转、缩放矩阵。

平移矩阵：

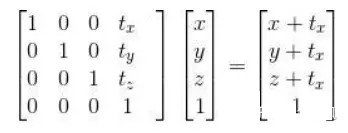
旋转矩阵：

缩放矩阵：

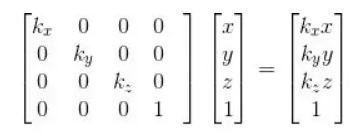
对于这些矩阵有一些特征：

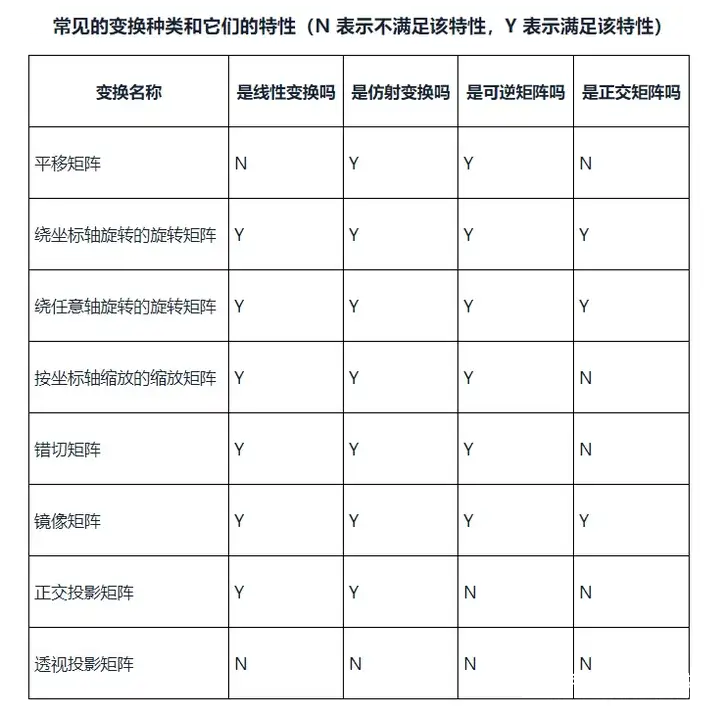
根据以上特征，可以得到一些计算顺序和技巧：

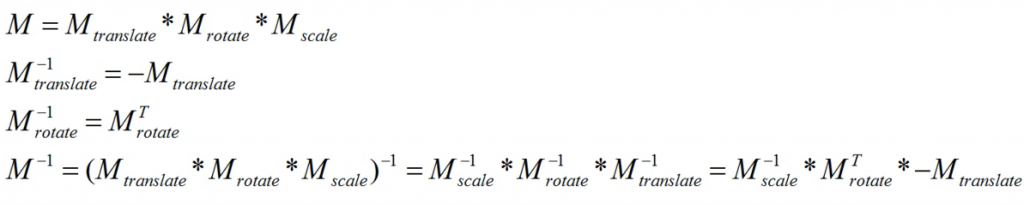
问：如果已知M，要逆推平移、旋转、缩放矩阵该怎么做呢？第四列的前三个数就是平移量，第一列数字的平方和开根号就是x的缩放，第二、三列对应y、z的缩放；给左上3×3子矩阵按列除以缩放值，得到的就是分解后的旋转矩阵。

模型变换和观察变换可以用上述矩阵组合得到，但是投影变换就没那么简单了。透视投影矩阵：

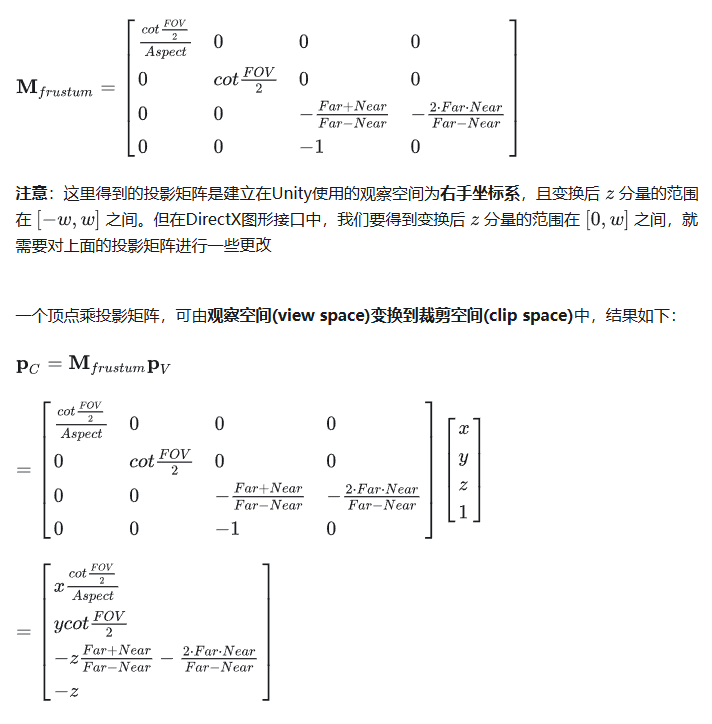
透视投影就是将视锥内的所有物体映射到一个(-1,-1,-1)到(1,1,1)的一个正方体空间内。

屏幕空间矩阵：

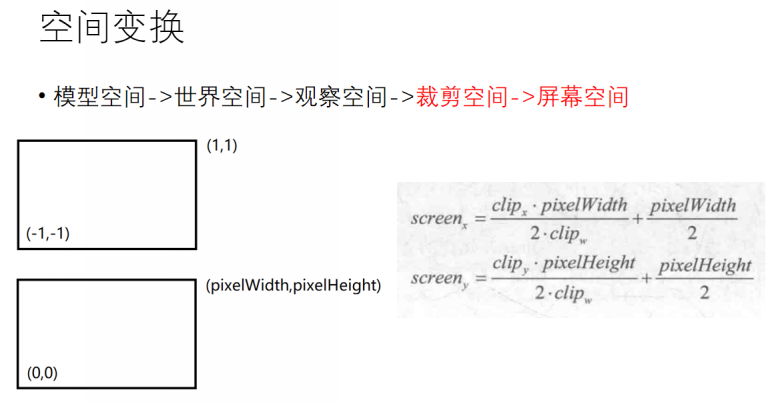
注意首先需要进行齐次除法（除以一个clipw），变换到NDC空间，再做屏幕空间的坐标转换。

综上，从模型空间到屏幕空间的变换顺序：

这里就是经典的mvp矩阵变换，先用m将模型空间转换为世界空间，再用v将世界空间转换为视角空间，再用p将视角空间变换为投影空间，最后用s将投影空间变换到屏幕空间。

最后再看一遍流程图：

【特殊情况】法线变换

我们知道顶点在做空间变换的时候，可以根据上述知识直接构造出一个空间变换矩阵M。而一个顶点的切线，是由两个临近顶点作差得到的，因此切线也可以使用矩阵M来进行空间变换。

法线是要保证变换前后一直和所有切线垂直的，假设法线的变换矩阵是M’，要满足：(M’n)·(Mt)=0，最终可以推导出M’=(M^-1)T，即空间变换矩阵的转置逆矩阵。

三、欧拉角与四元数

欧拉角使用3个旋转弧度来表示在x、y、z轴上的旋转，绕右向量为pitch、绕上向量为yaw、绕前向量为roll。

优点：直观、存储量小（3个float）、没有无效的欧拉角（任何一个欧拉角都有旋转意义）

缺点：多个欧拉角可能会对应同一个旋转角度（解决方案：yaw、roll限制±180°，pitch限制±90°）；万向节死锁（这个解决不了，所以只能使用后续的四元数）

理解三维空间的四元数旋转确实有点困难，可以从更简单的情况（二维空间的旋转）入手来辅助理解。如下图，在二维坐标系下，将二维坐标写成(实数,虚数)的形式，那么对坐标乘以一个虚数i就可以起到旋转90°的作用：

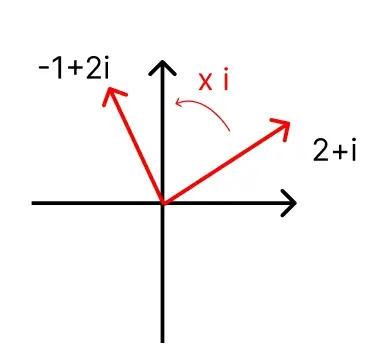
上面是90°的特殊情况，推广到一般情况，乘以一个a+bi，那么其实就是将向量的模长翻根号a^2+b^2倍，然后旋转arctan(b/a)角度，如下图所示：

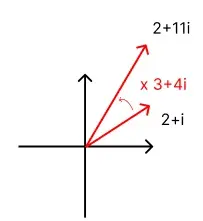
换一个说法，如果我们想要将一个向量(x,y)旋转θ°，那么只需要将(x+y*i)乘以一个(cosθ+sinθ*i)。（旋转二元数就是(cosθ,sinθ)）

那么过渡到三维空间，应该很快能想到：再加一维新的虚数j，即(a+bi+cj)。但是根据“毛球定理”，只加一维是不够的。什么是毛球定理呢，首先对于一个二维的圆，我们可以让圆上的每个点拥有一个向量场（例如全部点都向切线方向移动，最终的结果呈现就是旋转），这样就可以形成一个旋转后的圆。但是对于三维的球，我们同样希望球上的每个点拥有一个连续的向量，那么一定会有两个点的向量为0，这就是毛球定理。

换言之，如果是用a+bi+cj来构造三维的旋转，那么总会存在点压根转不起来。因此需要继续扩展一个维度dk，变成a+bi+cj+dk 也就是我们所说的四元数。接下来看一些运算规则：

在二维坐标系中，i表示沿不存在的z轴旋转90°，以此类推j和k就可以分别表示x、y轴旋转90°。可想而知，如果某个点沿x轴旋转90°，再沿y轴旋转90°，最后沿z轴旋转90°，那么这个点就会跑到相反数的位置上，即：

(x,y,z)*i*j*k=(-x,-y,-z)

由此可得ijk=-1

其余部分，i、j、k都严格遵守所有复数运算规则。此外，四元数也有逆，表示反向旋转。四元数的逆的计算方法就是使用四元数的共轭复数除以四元数的模。

那么最后来看一下四元数的应用。假如我们将目标点(x,y,z)按轴(b,c,d)旋转a°（注意这个轴的向量表示必须是单位向量），那么其旋转四元数就是：(cosθ,sinθ*b,sinθ*c,sinθ*d)，目标点(x,y,z)的四元数形式是(0,x,y,z)。计算方法为：目标点四元数左乘一个旋转四元数，并右乘一个旋转四元数的逆。

四、平面与射线

如何定义一个平面？假如我们选取一个点p0，其拥有一条法线n，那么所有与p0连接成向量后与n垂直的点p，就是该平面上的点：n(p-p0)=0；

换一种写法，令d=-np0那么满足np+d=0的p点就在该平面上，其中d/||n||就是平面到原点的距离。如果点p满足np+d＞0，则p点在平面外侧，反之在内侧。

射线的定义就是p(t)=p0+tu，其中p0是射线的端点，u是方向向量，t是该方向向量的延长量。

图形学光线追踪中，就需要根据当前光线和目标面进行求交测试，得出该射线是否能命中对应面、命中点在哪里。因此可以根据上述面和射线的数学定义来计算命中点的坐标：

p(t)=p0+tu np+d=0

n(p0+tu)+d=0

t=(-d-np0)/nu

射线求交的场景应用：

①光线追踪，需要枚举大量的三角面与当前光线进行求交测试；

②碰撞盒检测，需要枚举碰撞盒的最少4个面与视线或枪线进行求交测试；

③鼠标点选，需要先将鼠标点击的屏幕坐标转化到世界空间，即先乘Ms-1，再乘Mp-1，最后乘Mv-1，这样可以得到目标点在世界空间中的坐标，连接相机点就形成了鼠标点击后发出来的射线