Deprecated: Function create_function() is deprecated in /www/wwwroot/puluo.top/wp-content/plugins/codecolorer/lib/geshi.php on line 4698

引言

　　在之前的几篇blog中，主要介绍了最基础的两类渲染算法——光栅化和光线追踪。光栅化讲的是通过简易渲染管线来完成逐顶点计算和逐片元计算，光线追踪讲的是通过模拟光线传播行为来决定视口中每一个像素的颜色结果。而现代游戏引擎中，并不太可能使用这两种朴素算法，因此引入了一系列新型技术——实时渲染技术。

　　实时渲染追求的最终目标是以光栅化的速度完成光追级别的渲染效果，其一大特点是：追求效果大于理论——只要够快速，效果也够真实，即使违背一些理论也在所不惜。实时渲染技术已经广泛应用于各个建模软件与游戏引擎，尤其针对游戏行业，不可能使用离线渲染，然而又需要震撼玩家的画质，那么就不得不依赖于现代的实时渲染技术。

　　实时渲染技术分为很多方面，例如阴影、环境贴图、实时全局光照、实时PBR、实时光追等等，本篇先从最简单的实时阴影技术开始介绍。


shadowmap

　　shadowmap相对比较好理解。想想阴影出现的原因是什么？是因为光线照射的时候，被一些物体所遮挡，导致后面的物体表面无法接收到光线。因此假如我们需要判断某一点上是否有阴影，就要判断光线是否能够抵达到该点。

　　如何判断光线抵达的位置呢？我们可以切换到光源视角，即以光源为视线点，向周围环境去看，然后将看到的物体的深度写入到一张texture中（注意深度只保留绝对值最小值）。这个texture就是我们所说的shadowmap，其存入的深度的含义就是：光源向某个方向能照射到的最大距离。这一步的图示如下：

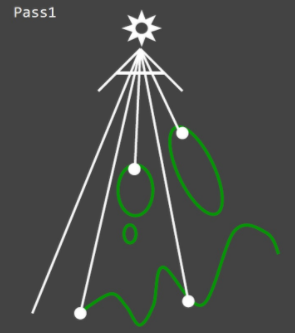
　　那么回到相机视角，如何确定我看到的某个点上是否有阴影呢？首先要计算出该点到光源的实际距离，然后查shadowmap上的深度，如果深度小于距离，那么说明光源在未到达对应点时就被挡住了，那么就需要产生阴影；如果深度等于距离，那么说明光线刚好抵达该点，就不需要产生阴影。这一步的图示如下：

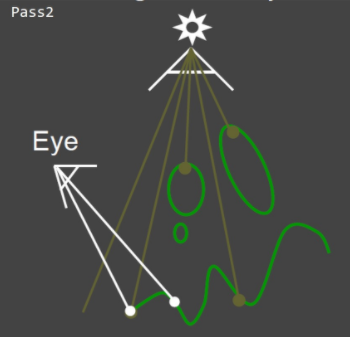
　　上图可以看到，有些目光打到的点恰巧也是光线打到的点，有些目光打到的点对应的光线却被提前遮挡。


　　好了，那我们便可以开始编程了。这里我以games202课程项目与《我的世界》光影为例，来编写代码。首先看一下games202中的项目，由于助教过于友好把框架几乎完全写好了，我们只需要补充一下函数就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
float useShadowMap(sampler2D shadowMap, vec4 shadowCoord){
  if(unpack(texture2D(shadowMap,shadowCoord.xy))<shadowCoord.z)return 0.0;
  return 1.0;
}

void main(void) {

  vec3 shadowCoord = (vPositionFromLight.xyz/vPositionFromLight.w)/2.0 +0.5;
  float visibility;
  visibility = useShadowMap(uShadowMap, vec4(shadowCoord, 1.0));
  vec3 phongColor = blinnPhong();
  gl_FragColor = vec4(phongColor * visibility, 1.0);
}

　　unpack是一种将压缩进texture的高精度浮点数解压出来的方法，不需要过多关注它的细节；texture2D(shadowMap,shadowCoord.xy)就是在shadowMap上采样，将对应点的深度信息采集出来；shadowCoord.z存的就是对应点距离光线的实际距离，如果深度小于实际距离，代表有阴影，那么最后着色的时候就应该是纯黑阴影（即visibility=0）。效果图如下：

　　结果发现这里有非常多的黑色条纹，地上和裙子上都有，san值狂掉。。。这里先不说为什么有这种现象，我们继续编写一下mc中的阴影效果。我们在shaderpacks中创建composite.fsh（片元着色器），编写如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#version 120

uniform sampler2D texture;
uniform sampler2D depthtex0;
uniform sampler2D shadow;

uniform float far;

uniform mat4 gbufferModelView;
uniform mat4 gbufferModelViewInverse;
uniform mat4 gbufferProjection;
uniform mat4 gbufferProjectionInverse;

uniform mat4 shadowModelView;
uniform mat4 shadowModelViewInverse;
uniform mat4 shadowProjection;
uniform mat4 shadowProjectionInverse;

varying vec4 texcoord;
vec4 getShadow(vec4 color, vec4 positionInWorldCoord) {
    // 我的世界坐标 转 太阳的眼坐标
    vec4 positionInSunViewCoord = shadowModelView * positionInWorldCoord;
    // 太阳的眼坐标 转 太阳的裁剪坐标
    vec4 positionInSunClipCoord = shadowProjection * positionInSunViewCoord;
    // 太阳的裁剪坐标 转 太阳的ndc坐标
    vec4 positionInSunNdcCoord = vec4(positionInSunClipCoord.xyz/positionInSunClipCoord.w, 1.0);

    // 太阳的ndc坐标 转 太阳的屏幕坐标
    vec4 positionInSunScreenCoord = positionInSunNdcCoord * 0.5 + 0.5;

    float currentDepth = positionInSunScreenCoord.z;    // 当前点的深度
    float closest = texture2D(shadow, positionInSunScreenCoord.xy).x;   // 离光源最近的点的深度

    // 如果当前点深度大于光照图中最近的点的深度 说明当前点在阴影中
    if(closest <= currentDepth) {
        color.rgb *= 0.5;   // 涂黑
    }
   
    return color;
}

void main() {
    vec4 color = texture2D(texture, texcoord.st);

    float depth = texture2D(depthtex0, texcoord.st).x;
   
    // 利用深度缓冲建立带深度的ndc坐标
    vec4 positionInNdcCoord = vec4(texcoord.st*2-1, depth*2-1, 1);

    // 逆投影变换 -- ndc坐标转到裁剪坐标
    vec4 positionInClipCoord = gbufferProjectionInverse * positionInNdcCoord;

    // 透视除法 -- 裁剪坐标转到眼坐标
    vec4 positionInViewCoord = vec4(positionInClipCoord.xyz/positionInClipCoord.w, 1.0);

    // 逆 “视图模型” 变换 -- 眼坐标转 “我的世界坐标”
    vec4 positionInWorldCoord = gbufferModelViewInverse * positionInViewCoord;

    color = getShadow(color, positionInWorldCoord);
   
    gl_FragData[0] = color;
}

　　这里的思路如下：对于某一个点，首先我们获得了一个屏幕坐标中的深度，这个深度值不能直接用，因为它是我们相机的屏幕坐标，我们想要的是它在光源视角下的屏幕坐标。所以我们首先要逐步将该点在相机下的屏幕坐标一路转化为世界坐标，然后再传入到getShadow函数中，将该点在世界下的坐标转化为光源视角下的屏幕坐标，这样就能得到了光线向该点照射的最大距离，即对应着shadowmap记录的深度值。再用这个深度值与对应点到光源的距离进行比较，如果有阴影就×0.5。最后的效果如下图所示：

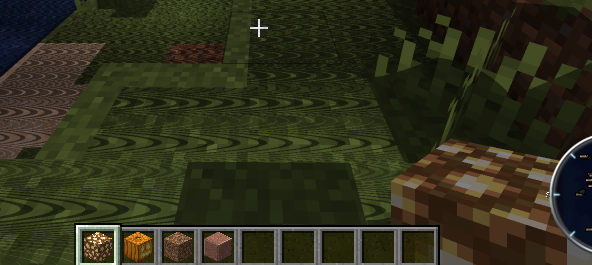
　　同样的问题出现了。。。一些莫名其妙的、类似摩尔纹一样的黑纹，到底是是什么导致了这个现象呢？我们知道，shadowmap的精度是有限的，意思是map上的每一个像素块都是有一定大小的，因此它记录的是某一小区块的深度信息。但是事实上，如果你斜着去看平面，那么每一个点的深度值都是不同的。如下图：

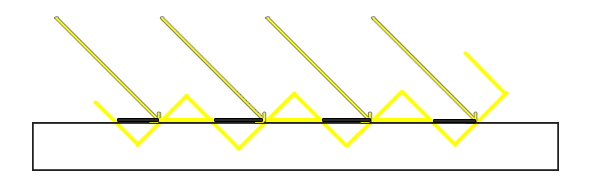
　　黄色代表了shadowmap记录的深度信息，那么你就会发现有些部分记录的深度在地面上方。这样，尽管光线本来可以打到地面上，但是记录的深度却比实际距离要小，那么程序就会认为这部分有阴影，就会产生阴影条纹。如图可以看到这种现象每隔一个像素都会出现一次，因此就会出现许多个条纹交替出现的现象。

　　那么如何解决这个问题呢？方法很简单，只需要在shadowmap上加一个bias偏移量，强行让浮在地面上方的值嵌入地面即可。对于games202可以这样修改：

1
2
3
4
float useShadowMap(sampler2D shadowMap, vec4 shadowCoord){
  if(unpack(texture2D(shadowMap,shadowCoord.xy))<shadowCoord.z-0.01)return 0.0;
  return 1.0;
}

　　对于mc光影可以这样修改：

1
2
3
4
5
6
// 如果当前点深度大于光照图中最近的点的深度 说明当前点在阴影中
    if(closest+0.001 <= currentDepth) {
        color.rgb *= 0.5;   // 涂黑
    }
   
    return color;

　　最后的效果图分别如下：


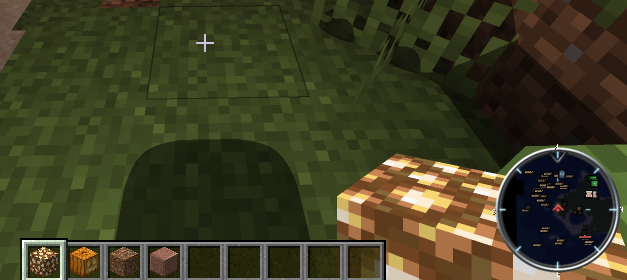
PCF软阴影

　　在前面的阴影存在一个问题，就是它的边缘过于锐利了，这样的阴影看起来非常生硬。因此，我们需要引入一种软阴影算法。它的算法也很好理解，那就是卷积。在《图像采样的空域频域原理》这篇文章中介绍了低通滤波和高斯模糊，其就是为了滤掉高频、锐利的信号，从而让图像的边缘部分变得柔和起来。软阴影同理，就是要让阴影像素与周围的像素作卷积，这样边缘部分的阴影就会变得柔和起来。

　　在games202的项目中，我们可以使用助教提供的采样模型进行周围像素的采样和卷积：

1
2
3
4
5
6
7
8
9
10
float PCF(sampler2D shadowMap, vec4 shadowCoord, float radius) {
  poissonDiskSamples(shadowCoord.xy);
  int count=0;
  for(int i=0;i<NUM_SAMPLES;i++)
  {
    float mapDepth=unpack(texture2D(shadowMap,shadowCoord.xy+poissonDisk[i]*radius/2048.0/*shadowCoord.xy*/));
    if(mapDepth+0.01>shadowCoord.z)count++;
  }
  return float(count)/float(NUM_SAMPLES);
}

　　卷积核大小取决于采样数量。对于每一个采样点都计算其颜色并叠加，最后将累加值除以采样数量，便得到了PCF的阴影颜色：

　　mc光影同理，采样周围点的遮挡情况，最后统一除以采样数量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int radius = 1;
    float sum = pow(radius*2+1, 2);
    float shadowStrength = 0.6 * (1-dis);
    for(int x=-radius; x<=radius; x++) {
        for(int y=-radius; y<=radius; y++) {
            // 采样偏移
            vec2 offset = vec2(x,y) / shadowMapResolution;
            // 光照图中最近的点的深度
            float closest = texture2D(shadow, positionInSunScreenCoord.xy + offset).x;  
            // 如果当前点深度大于光照图中最近的点的深度 说明当前点在阴影中
            if(closest+0.001 <= currentDepth && dis<0.99) {
                sum -= 1; // 涂黑
            }
        }
    }
    sum /= pow(radius*2+1, 2);
    color.rgb *= sum*shadowStrength + (1-shadowStrength);

　　效果如下图：


阴影数学解释

　　接下来我们将从数学角度来解释阴影的原理。既然是从数学角度，那么当然离不开渲染方程了。回顾在《BRDF光照模型与渲染方程》文章中介绍的渲染方程区域公式，其形式为：

$$L(x→out)=L_e(x→out)+\int_A^A f_r(x,in→out)L(y→-in)V(x,y)cos(\pmb N,\pmb {in})cos(\pmb {N_y},-\pmb {in})\frac{dA_y}{r_{xy}^2}$$

　　这里我们不考虑自发光的情况，所以简化一下变成：

$$L(x→out)=\int_A^A f_r(x,in→out)L(y→-in)V(x,y)cos(\pmb N,\pmb {in})cos(\pmb {N_y},-\pmb {in})\frac{dA_y}{r_{xy}^2}$$

　　现在这个式子没什么可操作性，因此我们需要引入一个近似的公式变换方法：

$$\int_A^Af(x)g(x)dx\approx\frac{\int_A^Af(x)dx}{\int_A^Adx}\int_A^Ag(x)dx$$

　　这个公式的含义就是，当两个函数f(x)和g(x)乘在一起后做积分，等价于f(x)积分归一化后再乘g(x)积分。根据这个近似变换，我们对渲染方程区域公式来做一点变换：

$$L(x→out)=\int_A^A f_r(x,in→out)L(y→-in)V(x,y)cos(\pmb N,\pmb {in})cos(\pmb {N_y},-\pmb {in})\frac{dA_y}{r_{xy}^2}$$

$$L(x→out)\approx\frac{\int_A^AV(x,y)dA_y}{\int_A^AdA_y}\int_A^A f_r(x,in→out)L(y→-in)cos(\pmb N,\pmb {in})cos(\pmb {N_y},-\pmb {in})\frac{dA_y}{r_{xy}^2}$$

　　近似后的公式其实就是：对于区域内的阴影状况进行一个积分，积分以后再归一化，然后乘上和阴影无关的渲染方程，就能得到某个点的亮度或出射光线的状况。这里其实就和PCF的思路有些相似：对阴影状况积分就好比对目标点周围的像素进行采样；除以一个空积分的归一化就好比除以采样数量点；两个积分相除就相当于得到了边缘阴影的一个平均值，这样就形成了柔和的边缘。


PCSS自适应软阴影

　　PCF是目前应用较为广泛的一种阴影，但它并不是效果最好的，因为它的滤波半径始终都是固定的，这也导致了阴影的各个部位都是一样“软”。然而真正的阴影会有这样一个特点：如果阴影距离遮挡物较近，则阴影很硬，反之则较软。因此如果要提升阴影的真实程度，必须要动态自适应滤波的卷积核尺寸。

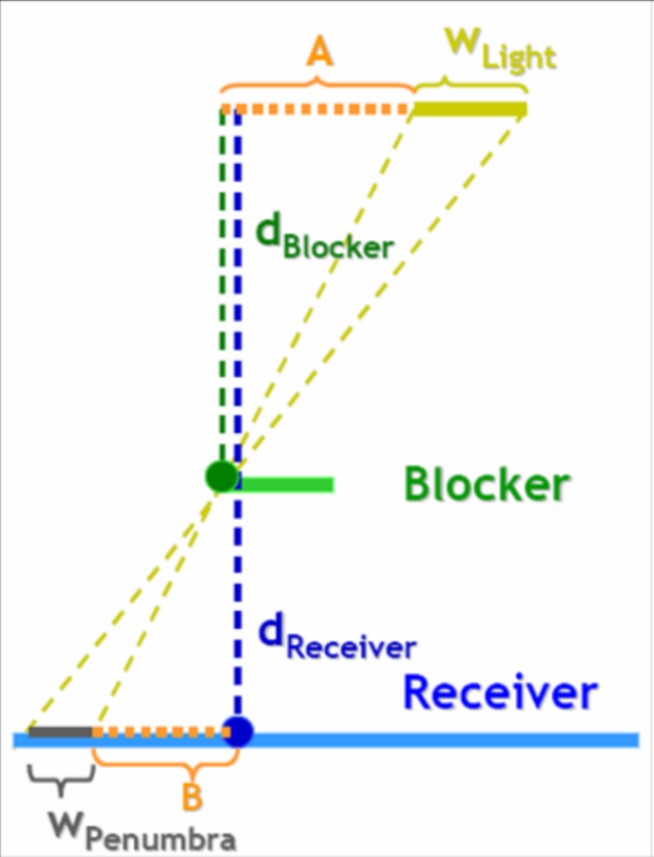
　　如图所示，生活中的光源一般不会是质点，而是具有一定的尺寸，长度为W_Light；W_Penumbra是半影尺寸，即由一个有尺寸的光源通过某个遮挡物留下的阴影范围。半影区域越大，那么阴影越柔和；若半影区域非常小，说明光源趋于理想点光源，此时阴影最硬。

　　那么在已知W_Light的情况下，可以根据相似三角形原理，从而推断出W_Penumbra的尺寸，然后根据该值来确定滤波的卷积核大小，这样就完成了阴影的不同区域柔和度不同的效果。那么算法的流程便为——计算d_Blocker和dReceiver；根据相似三角形原理计算W_Penumbra；构造卷积核并使用PCF算法滤波。（这个算法虽然提升了效果但是效率下降严重，在mc中几乎无法流畅运行，因此就不放代码和图了）


　　在PCSS提出以后，也有相应的优化算法如VSSM、MSM等算法被提出，但是开销和数学复杂性都较大，因此很少投入到应用当中。

一沙一世界，一花一天堂。君掌盛无边，刹那成永恒。