本篇IBL部分数学高能

引言

这一节我们来复现一下经典PBR模型，并引入IBL环境光照计算。这一章的数学公式和分析相对较多，难度较大，需要沉下心来阅读。

Part1. 微表面模型理论

之前我们使用过phong和blinn-phong模型，它们的BRDF都是漫反射项和镜面高光项的加和：

$$f_r = k_d * f_{lambert} + k_s * f_{phong/blinn-phong}$$

这些材质模型虽然可以提供不错的外观效果，但是它们终究有几个比较严重的问题：

1、局限性大，有很多现实的材质是上述模型无法通过调参拟合出来的；

2、模型没有模拟出真实物体表面的粗糙构造，现实很少有完全光滑的表面；

3、光照计算不完全基于物理，像blinn-phong经验模型甚至违反能量守恒。

所以后来诞生了微表面模型的概念，其核心思想是为表面假象了一个微观的粗糙结构：

这样起伏不平的表面意味着：微观法线的方向是具有随机性的，同时表面内部会有互相遮挡的现象，这样的结构比较清晰地模拟了现实世界中粗糙物体的性质。当然，由于它影响的是“微观法线”，所以实际上受影响的是高光的值（漫反射的值与法线无关）

cook-torrance就利用了这样的微表面结构，并提出了这样的一种BRDF：

$$f_r = k_d * f_{lambert} + f_{cook-torrance}$$

相当于在原本phong、blinn-phong的基础上，将高光分量的计算公式替换成了微表面分布下的高光计算公式。那么具体这个式子长什么样子呢？

$$f_{cook-torrance} = \frac{D*F*G}{4(\omega_o · n)(\omega_i · n)}$$

这里面提出了三个新概念，分别是D、F和G，这三个分量描述了一个完整微表面的性质。接下来我们详细探讨一下它们的性质。

1、法线分布函数D：

在讲D之前，我们回忆一下blinn-phong模型。blinn-phong模型比phong模型的提升点在于“半程向量”的概念，并且论证了半程向量与法线的cos值是描述高光强度的关键所在。微表面模型其实依旧沿用这样的准则，肯定半程向量的作用，只是由于微观表面是粗糙的，因此并非所有打在该点上的光线都会沿着相同的方向出射，那么半程向量的贡献就不再恒定了，而是有一部分会流失掉。

那么有多少能量会流失掉呢？取决于表面的粗糙程度。但表面趋近于完全光滑时，那么半程向量的贡献就是最大的；而如果表面非常粗糙，那么就会随着粗糙度的提升，半程向量的贡献越来越低。D函数就是要描述半程向量部分的最终贡献到底是多少。所以，一位叫做GGX的人提出了他的D项经验公式：

$$D = \frac{\alpha^2}{\pi((n · h)^2(\alpha^2 – 1) + 1)^2}$$

具体这个式子是怎么推出来的就不分析了，我们主要来分析一下它的性质。首先，当alpha非常大乃至接近1的时候，那么无论n · h等于多少，最后D的值都相差不大，这就意味着半程向量的高光贡献几乎被消除，那么材质表面处处都是相同的高光值：

而当alpha比较小乃至接近0的时候，只有当n · h非常接近1时，才能得到非常大的D值，否则D值一直会非常小，如下图所示：

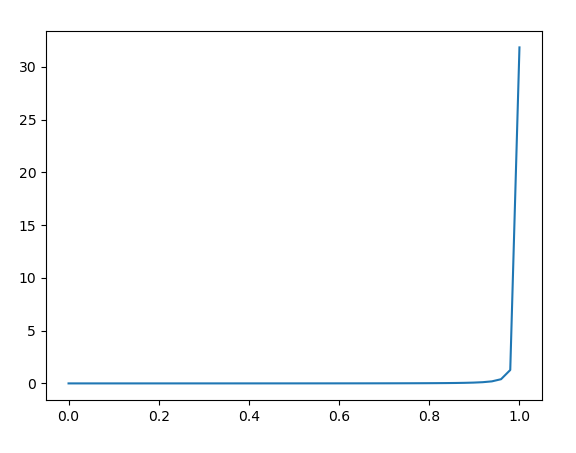
总结一下就是，alpha较大时，处处高光量相近；alpha较小时，半程向量与法线的cos值在接近1的地方会有极其闪亮的高光，而其他区域基本没任何高光。调节alpha的效果图示如下：

从图中我们能看到，ggx模型可以通过取不同的alpha值，来模拟出各种凝聚程度的高光亮点（亮点从小到大，亮度从强到弱）。有人会说blinn-phong也可以通过调整指数n来模拟亮点啊，但是事实上ggx这个模型可以保证真正意义上的能量守恒，即亮点凝聚了多少的能量，那么非亮点处就要损耗掉多少的能量，这是PBR的理论基础。

2、几何函数G

对于一个凹凸不平的表面，自然会有两个现象出现：一个是自阴影，一个是自遮挡。自阴影指的是本该照射到A点的光被B点挡住了，以至于A点没有接收到光线；自遮挡指的是A点本该反射到相机的光被B点挡住了，以至于相机没有接收到A点的着色结果。

首先我们考虑自阴影项。一般而言，某点能够接收到的光强由光线方向l和法线n作点乘得到，然而由于表面的粗糙性，所以某点实际上接收到的光强有一定比例会被其他点所挡住，从而形成阴影。我们可以想象，当光线垂直打向表面时，一般不会出现阴影；但是当光线平行地打向表面时非常容易形成阴影。而当平行地打向表面时形成地阴影到底有多重，使用k来决定：

$$G_{自阴影} = \frac{n · l}{(n · l)(1 – k) + k}$$

分析一下它的性质，当k=0时，G就等于1，此时平面相当于完全平整，表面没有任何互相遮挡形成的阴影；当k接近1时，G就等于n · l，意味着竖直入射到表面上的光线 获得光强更多（阴影更少），而水平入射到表面上的光线 获得光线更少（阴影更多，光全被挡没了）

接下来我们考虑自遮挡项。当我们以垂直表面的方向看向表面时，不会有哪个点会被挡住；但是当我们以水平地角度看向表面时，凹凸不平的表面就会互相遮挡，从而将反射给相机的光线消耗掉。而当平行地看向表面时遮挡现象到底有多重，也是使用k来决定：

$$G_{自遮挡} = \frac{n · v}{(n · v)(1 – k) + k}$$

你会发现自遮挡和自阴影本质上非常像，一个是从入射光考虑遮挡问题，一个是从出射光考虑遮挡问题，最后分析公式的方法也是一样的。

那么怎么将两个G项结合起来呢？我们直接用Smith法将两个乘在一起即可：

$$G_{自阴影} = \frac{n · l}{(n · l)(1 – k) + k} * \frac{n · v}{(n · v)(1 – k) + k}$$

调节k的效果图示如下：

仔细想一下会发现，alpha和k似乎拥有同质性，他们两个都是随着表面粗糙度的增加而增加。不过为了能量守恒，k并不等于alpha，在直接光照的情形下它们之间有这样一个关系：

$$k = \frac{(\alpha + 1)^2}{8}$$

在引入了自遮挡项后，我们可以看到材质表面不再是“有光就全亮，没光就全黑”的尴尬境地了，而是在有光的地方也会随着自遮挡效应的增强而慢慢衰减，最后慢慢过渡到没光的地方。

3、菲涅尔方程F

我们回忆一下上面讲的cook-torrance的BRDF：

$$f_r = k_d * f_{lambert} + f_{cook-torrance}$$

很快我们就发现一件事：k_s去哪里了？其实我们的菲涅尔项F就是k_s。为了能量守恒，我们要求k_d+F=1，那么具体F应该等于多少呢？这个就要由菲涅尔效应方程来决定了。菲尼尔效应我曾经在介绍BRDF的blog中有过介绍：辐射度算法与BxDF数学原理 – PULUO，它主要解释了当一根光线击中材质表面后，有多少比例（概率）会反射，有多少比例（概率）会透射。一般而言我们可以这样概括：当垂直看向表面时，透射率较大；当掠射平视表面时，反射率较大。一个近似的计算公式如下：

$$F = F_0 + (1 – F_0)(1 – (h · v))^5$$

当垂直看向表面时，h · v的值为1，此时F = F0，即k_s为F0，那么此时的k_d就为1 – F0；当掠视表面时，h · v的值为0，此时F = 1，即k_s为1，那么此时的k_d就为0。

有了上面三项后，我们就得到了cook-torrance的BRDF的完整写法：

$$f_r = k_d * f_{lambert} + f_{cook-torrance}$$

$$f_r = (1 – F) * \frac{c}{\pi} + F * \frac{D*G}{4(\omega_o · n)(\omega_i · n)}$$

这就是最基础的微表面模型公式。

Part2. PBR模型实现

现在我们其实可以将新的BRDF计算公式写入片元着色器了，但是还有一个小问题，那就是目前的可调参数意义不够明确。由于PBR材质最终是要交给美术去调整的，因此为每个参数赋予直观的意义是非常重要的。

对于PBR模型而言，最基础的参数是这些：albedo（漫反射分量）、metallic（金属度）、roughness（粗糙度）、specular（高光）。除了以上微表面模型相关的参数外，还会有一个ao（环境光遮蔽）、一个normalmap（法线贴图）。

albedo对应着漫反射项中的c，指材质表面本身的颜色；

metallic对应着菲涅尔项中的F0，当metallic拉到最大时，材质处处反射率恒为0，这样符合金属的性质；

roughness对应着D、G项中的alpha；

specular项要特别注意，它本身不存在于cook-torrance中，高光分量的比例应该完全由菲涅尔项F控制，只是有时候为了追求效果，我们可能会对高光量做一个额外的衰减，这个衰减系数就是specular。然而如果我们动了这一项，那么会导致材质模型有不可解释的能量损耗。

ao就是在建模软件中预先计算了ssao，然后把ssao的结果写入纹理中，这样我们就不需要在管线中额外耗费性能去算ao了。

现在pbr的基础理论就结束了。这里我们可以直接删掉片元着色器中blinn-phong材质的部分（我的渲染器日后不需要blinn-phong材质了，和pbr有点格格不入），来写一下pbr的材质。

首先是D、F、G的函数定义：

float D_GGX_TR(vec3 N, vec3 H, float a)
{
    float a2     = a*a;
    float NdotH  = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;

    float nom    = a2;
    float denom  = (NdotH2 * (a2 - 1.0) + 1.0);
    denom        = PI * denom * denom;

    return nom / denom;
}
float GeometrySchlickGGX(float NdotV, float k)
{
    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return nom / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx1 = GeometrySchlickGGX(NdotV, k);
    float ggx2 = GeometrySchlickGGX(NdotL, k);

    return ggx1 * ggx2;
}
vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
    return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}

这部分就是抄公式。接下来我们定义一下新的材质：

struct Material {
    vec4 diffuse;
    bool diffuse_texture_use;
    sampler2D diffuse_texture;

    vec3 specular;
    bool specular_texture_use;
    sampler2D specular_texture;

    float metallic;
    bool metallic_texture_use;
    sampler2D metallic_texture;

    float roughness;
    bool roughness_texture_use;
    sampler2D roughness_texture;

    bool normal_texture_use;
    sampler2D normal_texture;
    
    float ambient;
    bool ambient_texture_use;
    sampler2D ambient_texture;
}; 

而main函数就将blinn-phong的部分改成cook-torrance的部分：

void main()
{
    FragColor = vec4(0,0,0,1);
    BrightColor = vec4(0,0,0,1);

    vec4 diffuse_;
    if(material.diffuse_texture_use == true) {
        diffuse_ = texture(material.diffuse_texture, f_texcoord);
        diffuse_.rgb = pow(diffuse_.rgb,vec3(2.2));
    }
    else diffuse_ = material.diffuse;

    vec3 specular_;
    if(material.specular_texture_use == true) specular_ = vec3(texture(material.specular_texture, f_texcoord));
    else specular_ = material.specular;

    float metallic_;
    if(material.metallic_texture_use == true) metallic_ = texture(material.metallic_texture, f_texcoord).r;
    else metallic_ = material.metallic;

    float roughness_;
    if(material.roughness_texture_use == true) roughness_ = texture(material.roughness_texture, f_texcoord).r;
    else roughness_ = material.roughness;

    vec3 N = normalize(f_normal);
    if(material.normal_texture_use == true) {
        N = texture(material.normal_texture, f_texcoord).rgb;
        N = normalize(N * 2.0 - 1.0);
        N = normalize(f_TBN * N);
    }

    float ambient_;
    if(material.ambient_texture_use == true) ambient_ = texture(material.ambient_texture, f_texcoord).r;
    else ambient_ = material.ambient;

    vec3 F0 = mix(vec3(0.04), vec3(1.0), metallic_);
    vec3 V = normalize(cameraPos - f_FragPos);
    for(int i = 0; i < 1; i++){
        if(dl[i].color == vec3(0,0,0)) continue;
        vec3 L = normalize(-dl[i].dir);
        vec3 H = normalize(L + V);
        // cook-torrance brdf
        float NDF = D_GGX_TR(N, H, roughness_);        
        float G = GeometrySmith(N, V, L, roughness_);      
        vec3 F = fresnelSchlick(max(dot(H, V), 0.0), F0);
        vec3 kD = vec3(1.0) - F;

        vec3 nominator = NDF * G * F;
        float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.001; 
        vec3 specular = specular_ * nominator / denominator;

        // add to outgoing radiance Lo
        float shadow = cal_dir_shadow();
        float NdotL = max(dot(N, L), 0.0);                
        FragColor.rgb += (1 - shadow) * (kD * diffuse_.rgb / PI + specular) * dl[i].color * NdotL; 
    }
    for(int i = 0; i < 1; i++){
        if(pl[i].color == vec3(0,0,0)) continue;
        vec3 L = normalize(pl[i].pos - f_FragPos);
        vec3 H = normalize(L + V);
        float distance = length(pl[i].pos - f_FragPos);
        vec3 pl_color = pl[i].color / (pl[i].constant + pl[i].linear * distance + pl[i].quadratic * distance * distance);

        float NDF = D_GGX_TR(N, H, roughness_);        
        float G = GeometrySmith(N, V, L, roughness_);      
        vec3 F = fresnelSchlick(max(dot(H, V), 0.0), F0);
        vec3 kD = vec3(1.0) - F;

        vec3 nominator = NDF * G * F;
        float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.001; 
        vec3 specular = specular_ * nominator / denominator;

        // add to outgoing radiance Lo
        float NdotL = max(dot(N, L), 0.0);   

        float shadow = cal_point_shadow();
        FragColor.rgb += ((1 - shadow) * (kD * diffuse_.rgb / PI + specular) * pl_color * NdotL); 
    }
    FragColor.rgb += ambient_ * diffuse_.rgb;
    FragColor.a = diffuse_.a;

    float brightness = dot(FragColor.rgb, vec3(0.2126, 0.7152, 0.0722));
    if(brightness > 1.0)
        BrightColor = vec4(FragColor.rgb, 1.0);
}

然后当我将金属度调至1时，出现了这种景象：

奇怪，物体自身的颜色怎么没有了？

经过分析发现，当金属度为1时，F0=1，漫反射完全消失，所以漫反射贴图的颜色自然就没有了。我去翻了下learnOpengl，发现它做了个trick，就是将F0的范围钳制在(0.04, diffuse)之间，这样F0永远到不了1；同时k_d并不再是简单的1-F了，而是后续要再乘一个(1 – metallic)：

vec3 F0 = mix(vec3(0.04), diffuse_.rgb, metallic_);
...
vec3 kD = vec3(1.0) - F;
kD *= 1.0 - metallic_;

这样修改后，F0几乎不可能达到1，那么即使是金属度为1的地方也会存在部分漫反射了：

基于cook-torrance微表面模型的pbr材质就实现完成了。但是到这里还没有完全结束，因为真实的场景中压根不可能只有几盏光源，而是四面八方都会有光进来。在图形界中，我们可以使用环境贴图来作为四面八方的光源，来模拟真实环境。

Part3. HDR贴图

现在我们要来加载环境贴图。在前几章中我们成功加载了立方体贴图，但是事实上立方体贴图早已不是主流格式了，现在比较流行球状贴图，并且这类球状贴图基本都是exr\hdr等高动态范围图像格式。现在我们就先尝试将HDR贴图加载并渲染出来。

首先写一个加载HDR贴图的方法：

unsigned int loadHDR(const char* texturePath) {
    stbi_set_flip_vertically_on_load(true);
    int width, height, nrComponents;
    float* data = stbi_loadf(texturePath, &width, &height, &nrComponents, 0);
    unsigned int hdrTexture;
    if (data)
    {
        glGenTextures(1, &hdrTexture);
        glBindTexture(GL_TEXTURE_2D, hdrTexture);
        glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, width, height, 0, GL_RGB, GL_FLOAT, data);

        glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
        glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
        glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
        glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

        stbi_image_free(data);
    }
    else
    {
        std::cout << "Failed to load HDR image." << std::endl;
    }
}

当我们加载出HDR贴图后，我们要想办法将他变成立方体贴图。直接用CPU做转换是非常慢的，所以我们依旧靠跑渲染、运行shader来做转换。不同的是，这个shader全程只需要运行一次，将结果记录好后就再也不需要运行第二次了。

在转换之前，我们先把帧缓冲和纹理绑定好：

/*HDR的纹理模型设置*/
    unsigned int captureFBO, captureRBO;
    glGenFramebuffers(1, &captureFBO);
    glGenRenderbuffers(1, &captureRBO);
    glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
    glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
    glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512);
    glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, captureRBO);

    unsigned int envCubemap;
    glGenTextures(1, &envCubemap);
    glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
    for (unsigned int i = 0; i < 6; ++i)
    {
        glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 512, 512, 0, GL_RGB, GL_FLOAT, nullptr);
    }
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

现在我们定义了帧缓冲和六张纹理，便可以导入hdr图片并开始渲染啦：

/*HDR预读*/
    unsigned int hdrTexture = loadHDR("D:/mitsuba3_project/Part3/0.hdr");
    glm::mat4 captureProjection = glm::perspective(glm::radians(90.0f), 1.0f, 0.1f, 10.0f);
    glm::mat4 captureViews[] =
    {
       glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(1.0f,  0.0f,  0.0f), glm::vec3(0.0f, -1.0f,  0.0f)),
       glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(-1.0f,  0.0f,  0.0f), glm::vec3(0.0f, -1.0f,  0.0f)),
       glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f,  1.0f,  0.0f), glm::vec3(0.0f,  0.0f,  1.0f)),
       glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, -1.0f,  0.0f), glm::vec3(0.0f,  0.0f, -1.0f)),
       glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f,  0.0f,  1.0f), glm::vec3(0.0f, -1.0f,  0.0f)),
       glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f,  0.0f, -1.0f), glm::vec3(0.0f, -1.0f,  0.0f))
    };

    shader_hdr.use();
    shader_hdr.setInt("equirectangularMap", 0);
    shader_hdr.setMatrix("projection", captureProjection);
    glActiveTexture(GL_TEXTURE0);
    glBindTexture(GL_TEXTURE_2D, hdrTexture);

    glViewport(0, 0, 512, 512);
    glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
    for (unsigned int i = 0; i < 6; ++i)
    {
        shader_hdr.setMatrix("view", captureViews[i]);
        glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, envCubemap, 0);
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
        glBindVertexArray(skyboxVAO);
        glDrawArrays(GL_TRIANGLES, 0, 36);
    }
    glBindFramebuffer(GL_FRAMEBUFFER, 0);

通过这样的渲染，我们的envCubemap就有了6个方向的环境贴图记录了。当然，我们还没有写shader_hdr的着色器逻辑。片元着色器这里可以简单说一下，首先立方体的片元世界坐标其实就代表了射线的方向，我们可以根据射线方向计算出该方向在HDR贴图上的采样位置，计算方式是u = arctan(z / x)，v = arcsin(y)；然而这样计算出来的u的范围是(0,2Π)，v的范围是(0,Π)，所以得给他们分别乘(1/2Π)和(1/Π)：

////////////////////////顶点着色器////////////////////////
#version 330 core
layout (location = 0) in vec3 aPos;
out vec3 localPos;
uniform mat4 projection;
uniform mat4 view;

void main()
{
    localPos = aPos;  
    gl_Position =  projection * view * vec4(localPos, 1.0);
}

////////////////////////片元着色器////////////////////////
#version 330 core
out vec4 FragColor;
in vec3 localPos;
uniform sampler2D equirectangularMap;
const vec2 invAtan = vec2(0.1591, 0.3183);
vec2 SampleSphericalMap(vec3 v)
{
    vec2 uv = vec2(atan(v.z, v.x), asin(v.y));
    uv *= invAtan;
    uv += 0.5;
    return uv;
}

void main()
{       
    vec2 uv = SampleSphericalMap(normalize(localPos)); // make sure to normalize localPos
    vec3 color = texture(equirectangularMap, uv).rgb;

    FragColor = vec4(color, 1.0);
}

这样就可以把6个方向的结果准确地写入到cubemap的6张方向贴图上了。

最后一步，还记得我们之前渲染过立方体贴图吗？将那里送入的cubemap直接改成刚才渲染得到的cubemap即可。最终效果如下：

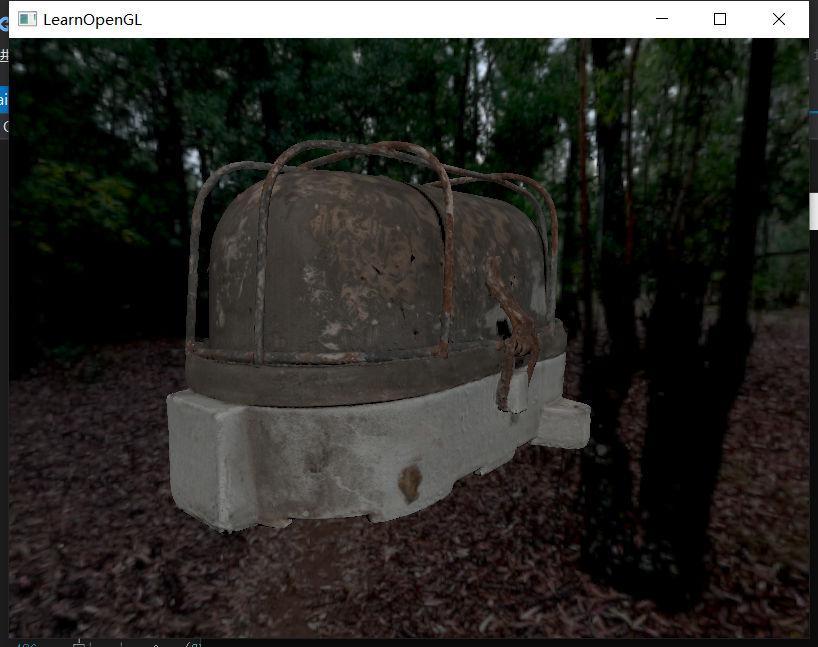
Part4. IBL-漫反射辐照

对于一个只有点光源和平行光源的场景，其片元的光照计算都比较容易，只需要枚举每一盏灯对其的光照贡献即可。然而环境贴图可以理解为无数个光源（或者环境贴图像素数量的光源），对环境贴图上每一个像素进行逐个计算显然不现实。所以有一些特殊的技法来辅助我们估计环境对于每一个片元的光照贡献。

首先再次回顾我们的渲染方程：

$$L(x→out)=Emission + \int_\omega^\omega f_r(x,in→out)L(x←in)cos(N,in)d\omega$$

$$=Emission + \int_\omega^\omega (k_d * f_{lambert} + f_{cook-torrance})L(x←in)cos(N,in)d\omega$$

$$=Emission + \int_\omega^\omega (k_d * f_{lambert})L(x←in)cos(N,in)d\omega + \int_\omega^\omega f_{cook-torrance}L(x←in)cos(N,in)d\omega$$

不考虑自发光项，我们成功将渲染方程分割为两部分，左边是漫反射项的积分，右边是镜面项的积分。这个part我们来分析一下如何计算左边漫反射项的积分：

$$L_{漫反射项} = \int_\omega^\omega (k_d * f_{lambert})L(x←in)cos(N,in)d\omega$$

由于w是立体角，没办法直接指明采样方向，我们可以将立体角的微分 拆分成 方位角和天顶角的微分形式：

$$\int_{2\pi} f(\omega)d\omega = \int_0^{2\pi}\int_0^{\frac{\pi}{2}}f(\theta,\phi)sin\theta d\theta d\phi$$

所以漫反射部分的渲染方程可以改写成：

$$L_{漫反射项} = \int_0^{2\pi}\int_0^{\frac{\pi}{2}}(k_d * f_{lambert})L(x←in)cos(N,in)sin\theta d\theta d\phi$$

$$L_{漫反射项} = k_d * f_{lambert} * \int_0^{2\pi}\int_0^{\frac{\pi}{2}}L(x←in)cos(N,in)sin\theta d\theta d\phi$$

这个积分就是我们要处理的最终式子了。接下来我们讨论一下如何去解它。

之前我曾经写过一篇蒙特卡洛积分与重要性采样的blog，理论上来说这里依然可以使用蒙特卡洛积分的思路，通过大量的随机采样来估计积分值，然而事实上我们并不打算这样做，这是因为漫反射的反射空间是一整个半球，是一个非常大的采样域，因此如果我们使用随机采样，每个片元实际的采样分布都不一样，最后每个点的收敛程度也就都不一样，会导致大量噪声的出现。

这里我们希望使用黎曼和的思路，即等间距地采样环境贴图上的像素，采样的区域覆盖整个半球。这相当于是一种“固定采样”，即每一个采样点在哪里都已经提前决定好了。固定的采样方案意味着每个片元计算的积分结果收敛程度极其接近，就不会产生噪声了。

黎曼和的具体思路其实很简单，就是当我们要求一个不规则图形的面积的时候，可以把他细分成无数个细小的四边形，最后将他们的面积加在一起：

$$f = \int_a^b g(x)dx$$

$$f ≈ \frac{b-a}{k}\sum_{n=0}^k g(x)$$

按照这个思路，我们也可以将漫反射项的积分拆成若干个细小区域，最后取黎曼和。根据漫反射项的积分形式，phi角是从0到Π/2作积分，theta角是从0到2Π作积分，那么我们可以把phi角的取值分割成n2份，把theta的取值分割成n1份，逐个进行采样。

$$L_{漫反射项} = k_d * f_{lambert} * \int_0^{2\pi}\int_0^{\frac{\pi}{2}}L(x←in)cos(N,in)sin\theta d\theta d\phi$$

$$L_{漫反射项} ≈ k_d * f_{lambert} * \sum_{p = 0}^{n_1}\sum_{q = 0}^{n_2}L(x←in)cos(N,in)sin\theta d\theta d\phi$$

$$L_{漫反射项} ≈ k_d * f_{lambert} * \frac{2*\pi}{n_1} * \frac{\pi}{2*n_2} * \sum_{p = 0}^{n_1}\sum_{q = 0}^{n_2}L(x←in)cos\theta sin\theta$$

$$L_{漫反射项} ≈ k_d * \frac{c*\pi}{n_1*n_2} * \sum_{p = 0}^{n_1}\sum_{q = 0}^{n_2}L(x←in)cos\theta sin\theta$$

那么现在的思路就非常清晰了，我们想要计算环境贴图对某片元的漫反射项贡献，就需要沿着该片元的法线方向形成一个半球，在这个半球上等距地采样，其中theta取值从0到2Π，间距为2Π/n1；phi取值从0到Π/2，间距为Π/(2*n2)；每次采样结果都代入到上面推出来的式子中，最后加和，便是环境贴图对该片元漫反射项的全部贡献。

现在我们继续考虑一个问题：这种半球采样，真的有必要放到pbr的片元着色器里一遍又一遍去做吗？仔细观察就会发现，漫反射项的积分部分其实和材质属性、和视线方向都没有任何关系！它只和片元的法线方向有关，一个法线方向决定了哪个半球对自己有光照贡献，而该半球的积分可以通过黎曼和的形式来得到。这就意味着：我们可以通过预计算，提前算出每个法线方向的积分（黎曼和）结果！

所以我们要做一步预处理，开一个和环境贴图一样尺寸的贴图，称为“预卷积贴图”，这个贴图上的像素记录着：当某片元的法线方向指向该像素时，环境贴图对其漫反射项的贡献积分结果是多少。这样当我们pbr的片元着色器要计算环境光贡献时，直接根据法线采样预卷积贴图就可以得到积分结果了，节省了大量的性能！

现在我们来创建一个卷积shader，来将我们的立方体贴图处理成“预卷积贴图”：

#version 330 core
out vec4 FragColor;
in vec3 localPos;

uniform samplerCube environmentMap;

const float PI = 3.14159265359;

void main()
{
    vec3 normal = normalize(localPos);
    vec3 irradiance = vec3(0.0);  
    vec3 up    = vec3(0.0, 1.0, 0.0);
    vec3 right = cross(up, normal);
    up = cross(normal, right);
    float sampleDelta = 0.025;
    float nrSamples = 0.0; 
    for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta)
    {
        for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
        {
            //spherical to cartesian (in tangent space)
            vec3 tangentSample = vec3(sin(theta) * cos(phi),  sin(theta) * sin(phi), cos(theta));
            //tangent space to world
            vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N; 

            irradiance += texture(environmentMap, sampleVec).rgb * cos(theta) * sin(theta);
            nrSamples++;
        }
    }
    irradiance = PI * irradiance * (1.0 / float(nrSamples));

    FragColor = vec4(irradiance, 1.0);
}

这部分代码还是蛮关键的，所以我来仔细分析一下：

首先我们的“预卷积贴图”上的像素，记录的是当物体上某片元的法线方向指向该像素时，环境贴图对其漫反射项的贡献积分结果是多少，因此我们枚举到的“预卷积贴图”的片元坐标，就是到时候物体上片元的法线方向。

接下来我们开始求黎曼和，按照公式将phi和theta分解成若干份，取样间距是sampleDelta，每次采样完phi和theta后可以根据球坐标公式求出具体的方位向量。然而这里有一个大坑：这个方位向量其实是切线空间的，我们需要将其转化到世界空间！我们来分析一下如何转化。

在切线空间中，切线、副切线、法线分别代表了(1,0,0)，(0,1,0)，(0,0,1)三个轴，假设我们的方位向量在切线空间下是(x,y,z)，那么它可以写成(x * T切 + y * B切 + z * N切)的形式；

现在考虑T、B、N在世界空间中的方向，N的世界空间方向我们已经提前知道了（就是片元坐标），而T、B都不知道。但是事实上，半球是处处沿着法线对称的，所以T和B指向哪里是可以随意指定的，只要保证TBN互相正交垂直即可。那么我们就假设B是(0,1,0)，然后用N和B叉乘得到T，再用T和N叉乘得到正交化的B即可。那么，方向向量的世界空间下的表示就是(x * T世 + y * B世界 + z * N世)了。这就是”vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N”这句代码所做的事情，将方位向量转换到世界空间。

接下来我们就沿着方位向量去采样环境贴图，然后把结果累加即可，最后除以(n1*n2)，当然其实nrSamples就是n1*n2。

然后老样子，我们绑定新纹理，然后跑一遍shader渲染来写入这个预卷积贴图：

/*预处理，漫反射项的卷积*/
    unsigned int hdrCubemap_convolution;
    glGenTextures(1, &hdrCubemap_convolution);
    glBindTexture(GL_TEXTURE_CUBE_MAP, hdrCubemap_convolution);
    for (unsigned int i = 0; i < 6; ++i)
    {
        glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F,
            128, 128, 0, GL_RGB, GL_FLOAT, nullptr);
    }
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
    glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
    glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
    glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 128, 128);
    glViewport(0, 0, 128, 128);
    shader_hdr_convolution.use();
    shader_hdr_convolution.setInt("environmentMap", 0);
    shader_hdr_convolution.setMatrix("projection", captureProjection);
    glActiveTexture(GL_TEXTURE0);
    glBindTexture(GL_TEXTURE_CUBE_MAP, hdrCubemap);
    for (unsigned int i = 0; i < 6; ++i)
    {
        shader_hdr_convolution.setMatrix("view", captureViews[i]);
        glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, hdrCubemap_convolution, 0);
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
        glBindVertexArray(skyboxVAO);
        glDrawArrays(GL_TRIANGLES, 0, 36);
    }
    glBindFramebuffer(GL_FRAMEBUFFER, 0);

最后结果如下：

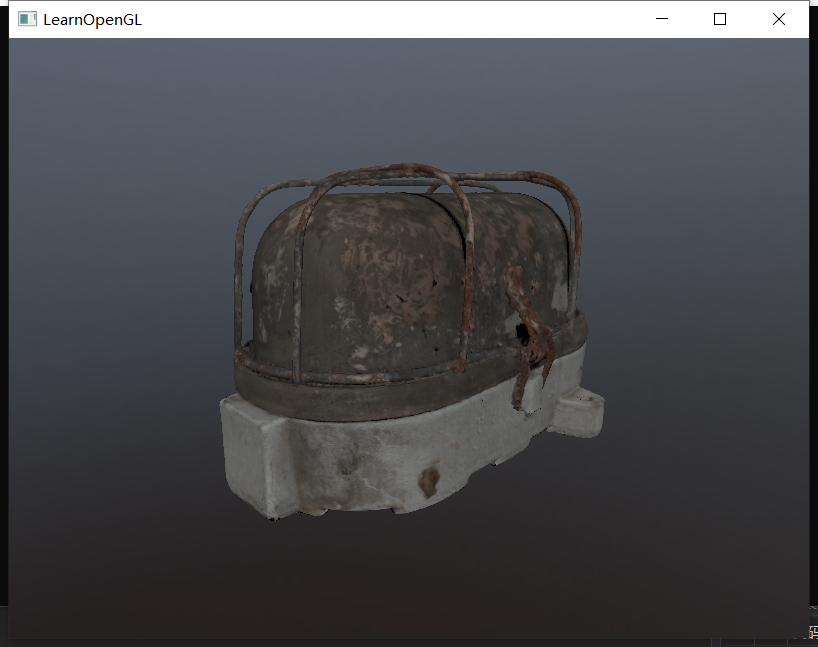
可以看到环境贴图已经完成了卷积。当然我发现卷积速度很慢，这样每次导入环境贴图都要等很久，所以我们可以进一步降低预卷积贴图的分辨率，或者降低片元着色器中采样的频率（增大采样间隔）。

现在我们要让pbr的着色器去采样这张预卷积贴图，来完成环境光的计算。由于预卷积贴图记录了除k_d、c外的式子结果，所以当我们取样到预卷积结果后乘一个k_d再乘一个漫反射颜色即可。但是，我们知道k_d是由菲涅尔项F推算出来的，而菲涅尔项F需要光照方向信息。当前环境光的光照是四面八方来的，我们怎么求菲涅尔项呢？这里learnOpengl给了这么个方案，虽然我不是很理解为啥可以这么做：

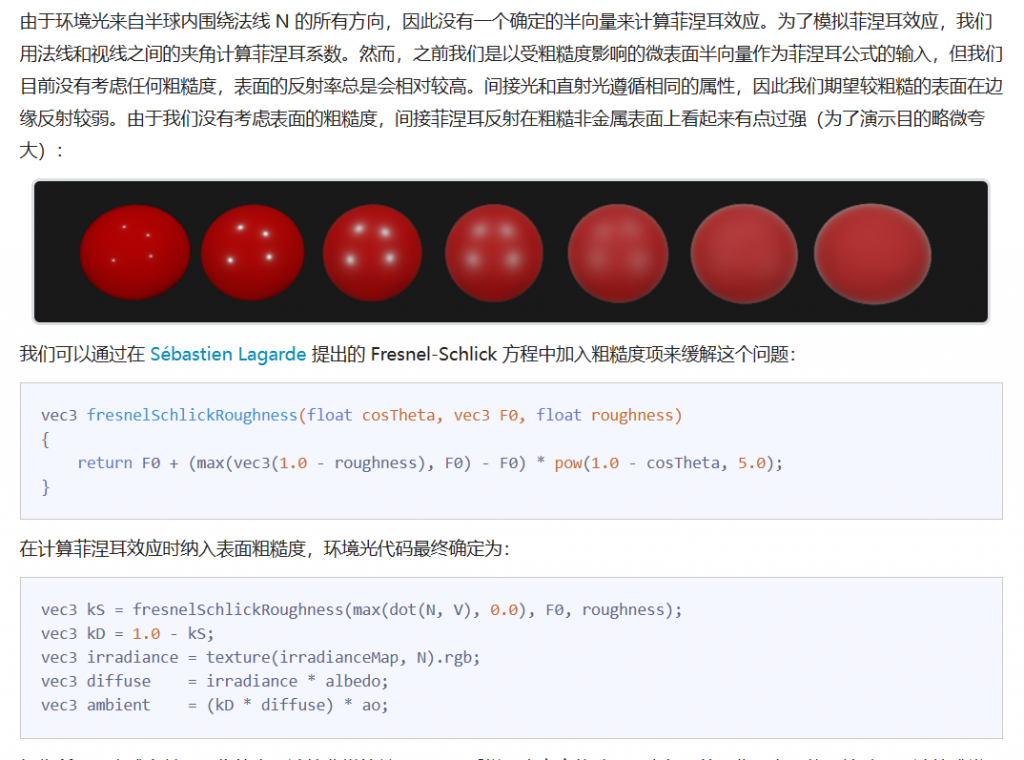
据说unreal里就是这么做的，我们姑且认为这是一个trick（毕竟大家都解释不了为啥可以这样干。。。）

vec3 kS = fresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness_); 
    vec3 kD = 1.0 - kS;
    kD *= 1.0 - metallic_;
    FragColor.rgb += ambient_ * kD * texture(diffuse_convolution, N).rgb * diffuse_.rgb;
    FragColor.a = diffuse_.a;

最后的结果就是这样的：

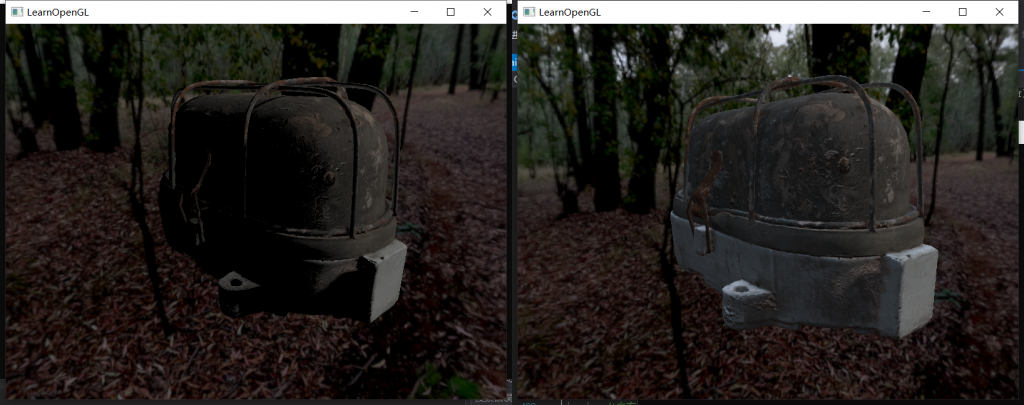
左侧是没有加环境光的，右边是考虑了环境光贡献的。

这样漫反射项的环境光贡献就计算完毕了。然而，噩梦刚刚开始，因为接下来要计算镜面反射项的环境光贡献，这可能会是截至目前最难、最晦涩的一个Part！

Part5. IBL-镜面反射辐照

回忆一下我们拆分的渲染方程：

$$\int_\omega^\omega (k_d * f_{lambert})L(x←in)cos(N,in)d\omega + \int_\omega^\omega f_{cook-torrance}L(x←in)cos(N,in)d\omega$$

左侧的漫反射积分已经在上一个Part中解决了，接下来我们要考虑右侧的积分该如何计算：

$$\int_\omega^\omega f_{cook-torrance}L(x←in)cos(N,in)d\omega$$

$$\int_\omega^\omega F * \frac{D*G}{4(\omega_o · n)(\omega_i · n)}L(x←in)cos(N,in)d\omega$$

其实思路可以沿袭漫反射辐照的思路，就是我们仍然需要预计算一些环境贴图，最后在pbr的片元着色器采样即可。但是这一次，并没有那么顺利了，这是因为积分项的分母中出现了w_o（出射立体角），所以就不能只对一个w_i作积分了。然而想对w_i和w_o同时作积分那简直是天方夜谭，所以unreal又提出了一个trick：通过分割求和近似法，将积分项拆解成两项相乘的形式：

$$\int_\omega^\omega F * \frac{D*G}{4(\omega_o · n)(\omega_i · n)}L(x←in)cos(N,in)d\omega≈\int_\omega^\omega F * \frac{D*G}{4(\omega_o · n)(\omega_i · n)}cos(N,in)d\omega * \int_\omega^\omega L(x←in)d\omega$$

所以现在我们又成功将问题分解为了两部分。后半部分是对L光线做积分，代号“光源积分”；前半部分是对DFG那部分做积分，代号“DFG积分”。接下来我们分别解析一下它们的解法。

1、光源积分

这部分长这样：

$$\int_{2\pi} L(x←in)d\omega$$

看起来是一个非常简单的积分，我们直接使用漫反射辐照那节的方法就好了，做一次预卷积即可。

如果这么想，就已经中计了。为什么呢？我们回忆一下微表面模型中的D项（法线分布函数），我们知道在粗糙度很低的情况下，只有n · h非常接近1的片元才能最大化保留入射的光线能量：

其他片元的入射能量几乎全部损耗掉了。这就意味着：对于每个片元而言，只有一部分方向进来的环境光可以被保留，而并非整个半球方向的环境光都有实质贡献，所以我们采样要专挑贡献大的地方采，不能采没有贡献的光。越粗糙的表面，有贡献的光的范围越大；越光滑的表面，有贡献的光的范围越小。

那么结论就是，当我们做预卷积贴图的时候，不同粗糙度的采样区域是不同的，越粗糙的材质 采样范围越大；越光滑的材质 采样范围越小：

所以我们的思路就变成了：

提前给粗糙度的值分5个档，对于每档都做一张对应的预卷积贴图，贴图上的像素存储的是 当视线击中材质后的反射向量指向该像素时，环境光照的贡献积分值是多少；不同档的预卷积贴图使用的采样方案当然也有区别。

首先我们绑定一下新的mipmap纹理：

/*预处理，镜面反射项的卷积*/
    unsigned int hdrCubemap_mipmap;
    glGenTextures(1, &hdrCubemap_mipmap);
    glBindTexture(GL_TEXTURE_CUBE_MAP, hdrCubemap_mipmap);
    for (unsigned int i = 0; i < 6; ++i)
    {
        glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 128, 128, 0, GL_RGB, GL_FLOAT, nullptr);
    }
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
    glGenerateMipmap(GL_TEXTURE_CUBE_MAP);

    shader_hdr_mipmap.use();
    shader_hdr_mipmap.setInt("environmentMap", 0);
    shader_hdr_mipmap.setMatrix("projection", captureProjection);
    glActiveTexture(GL_TEXTURE0);
    glBindTexture(GL_TEXTURE_CUBE_MAP, hdrCubemap);

    glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
    unsigned int maxMipLevels = 5;
    for (unsigned int mip = 0; mip < maxMipLevels; ++mip)
    {
        unsigned int mipWidth = 128 * std::pow(0.5, mip);
        unsigned int mipHeight = 128 * std::pow(0.5, mip);
        glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
        glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, mipWidth, mipHeight);
        glViewport(0, 0, mipWidth, mipHeight);

        float roughness = (float)mip / (float)(maxMipLevels - 1);
        shader_hdr_mipmap.setFloat("roughness", roughness);
        for (unsigned int i = 0; i < 6; ++i)
        {
            shader_hdr_mipmap.setMatrix("view", captureViews[i]);
            glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0,
                GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, hdrCubemap_mipmap, mip);

            glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
            glBindVertexArray(skyboxVAO);
            glDrawArrays(GL_TRIANGLES, 0, 36);
        }
    }
    glBindFramebuffer(GL_FRAMEBUFFER, 0);

接下来我们就分析一下，不同粗糙度对应的预卷积贴图的“采样方案”具体应该是什么样的。

对于一个比较粗糙的表面而言，各个方向来的入射光最终都会对出射光有贡献，但是这种贡献并不是均衡的，而是越靠近镜面反射方向的反射光能量越大。换个角度讲，当我们看向某个片元时，从镜面方向射入该片元的光照贡献最大，所以我们就更应该多去采镜面方向来的光源；而对于非镜面方向摄入该片元的光线，它们也有一定贡献，不过会有很大衰减，所以我们就以更小的概率去采样这些方向来的光源。

不错，相信你一定想到了一个思路，那就是重要性采样。对于贡献大的地方，采样率加大；对于贡献小的地方，采样率减小；对于没贡献的地方基本不要去采。其原理我曾经在蒙特卡洛积分与重要性采样 – PULUO介绍过。

所以本质上，我们就要创建关于ggx模型的重要性采样方法，根据这个采样方式去采样环境光，最后来拟合“光源积分”的估计值。接下来我们来看一下ggx的重要性采样是什么样的，由于ggx包含了D、F、G，而F和G并不好计算重要性采样公式，所以我们只分析D项。

对于D项，计算公式是：

$$D = \frac{\alpha^2}{\pi * (cos^2\theta_h)(\alpha^2 – 1) + 1)^2}$$

我们曾讲过，当一个函数的概率密度函数pdf和原函数的走势相同时，采样方差最小、收敛最快。所以pdf就是在原函数的基础上乘一个k值，这个k值是归一化分量：

$$p(\theta,\phi) = k * \frac{\alpha^2}{\pi * (cos^2\theta_h)(\alpha^2 – 1) + 1)^2}$$

现在这个式子里有theta也有phi，是一个联合概率分布，我们直接将phi消掉：

$$p(\theta) = \int_0^{2\pi}p(\theta,\phi) d\phi = 2\pi * p(\theta,\phi) = \frac{2*k*\alpha^2}{(cos^2\theta_h)(\alpha^2 – 1) + 1)^2}$$

根据pdf的性质，我们对自变量的全部定义域作积分，最后的积分结果必须是1，这样我们就要可以接出来k的大小了：

$$\int_0^{\frac{\pi}{2}} p(\theta)d\theta = 1$$

$$\int_0^{\frac{\pi}{2}} \frac{2*k*\alpha^2}{(cos^2\theta_h)(\alpha^2 – 1) + 1)^2}d\theta = 1$$

具体怎么解我不会（大一高数白给），所以我就直接去偷了下答案，最后解出来的k是cosθ。所以我们的pdf就是：

$$p(\theta) = \frac{2*cos\theta *\alpha^2}{(cos^2\theta_h)(\alpha^2 – 1) + 1)^2}$$

那么根据重要性采样的思路，我们应该求出他的CDF表达式，再取反函数，这样就可以生成重要性采样的方案了：

$$CDF = \int_0^{\frac{\pi}{2}} p(\theta)d\theta$$

$$CDF = \int_0^{\frac{\pi}{2}} \frac{2*cos\theta*\alpha^2}{(cos^2\theta_h)(\alpha^2 – 1) + 1)^2}d\theta$$

$$CDF = \frac{\alpha^2}{(\alpha^2-1)^2 cos^2\theta’ + (\alpha^2-1)} – \frac{1}{\alpha^2 – 1}$$

取反函数就是：

$$\theta_h = arccos\sqrt{\frac{1 – \xi_2}{\xi_2(\alpha^2-1)+1}}$$

现在θh的采样方案我们就有了，至于φ，可以均匀取样：

$$\phi_h = 2\pi\xi_1$$

好了，这样我们就得到了要采样的半程向量的方向，当然我们依然要将其从切线空间转换到世界空间中，然后根据世界空间下的视线方向和半程向量，反算光线的入射方向即可。

#version 330 core
out vec4 FragColor;
in vec3 localPos;

uniform samplerCube environmentMap;
uniform float roughness;

const float PI = 3.14159265359;
float RadicalInverse_VdC(uint bits) 
{
    bits = (bits << 16u) | (bits >> 16u);
    bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
    bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
    bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
    bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
    return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
    return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}  
vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)
{
    float a = roughness*roughness;

    float phi = 2.0 * PI * Xi.x;
    float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
    float sinTheta = sqrt(1.0 - cosTheta*cosTheta);

    // from spherical coordinates to cartesian coordinates
    vec3 H;
    H.x = cos(phi) * sinTheta;
    H.y = sin(phi) * sinTheta;
    H.z = cosTheta;

    // from tangent-space vector to world-space sample vector
    vec3 up        = abs(N.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
    vec3 tangent   = normalize(cross(up, N));
    vec3 bitangent = cross(N, tangent);

    vec3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
    return normalize(sampleVec);
}

void main()
{       
    vec3 N = normalize(localPos);    
    vec3 R = N;
    vec3 V = R;

    const uint SAMPLE_COUNT = 1024u;
    float totalWeight = 0.0;   
    vec3 prefilteredColor = vec3(0.0);     
    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
    {
        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
        vec3 H  = ImportanceSampleGGX(Xi, N, roughness);
        vec3 L  = normalize(2.0 * dot(V, H) * H - V);

        float NdotL = max(dot(N, L), 0.0);
        if(NdotL > 0.0)
        {
            prefilteredColor += texture(environmentMap, L).rgb * NdotL;
            totalWeight      += NdotL;
        }
    }
    prefilteredColor = prefilteredColor / totalWeight;

    FragColor = vec4(prefilteredColor, 1.0);
}  

这里的Hammersley是一个低差异序列的采样器，可以让随机采样分布得更均匀一些，具体原理就不说了。在main函数中，我们开始做重要性采样，每次根据采样器生成两个采样数，并根据上述重要性采样的公式得到半程向量的采样方向（别忘了要从切线空间转化到世界空间），从而得到采样的入射光线方向，最后去环境贴图上进行取样混合即可。

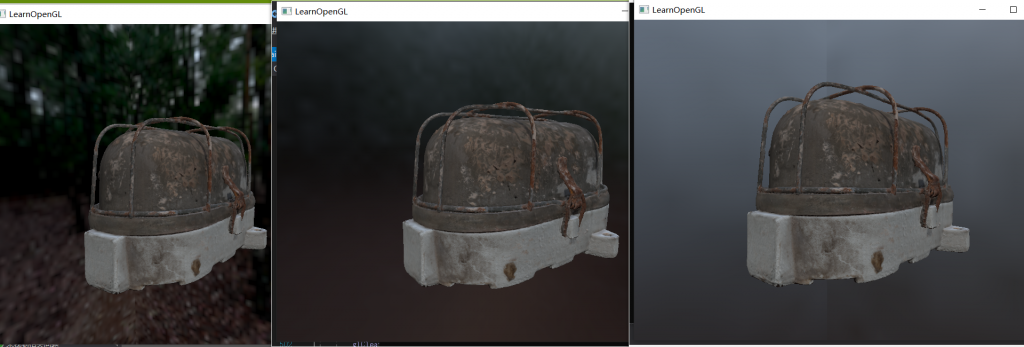
如图所示，分别是lod=0、lod=1、lod=3的结果。当然我们发现当lod比较大的时候，会出现一道分界线，

我们可以用glEnable(GL_TEXTURE_CUBE_MAP_SEAMLESS)来消除。

现在，我们终于完成了光源积分的拟合，然后接下来，我们来看一下DFG项的积分拟合。

2、DFG积分

这部分长这样：

$$\int_{2\pi} fr*cos(N,in)d\omega$$

这个积分的参数有很多，例如n · w_o、粗糙度、F_0。如果对三个变量作联合预处理，那计算量太大了。因此我们决定给它改一改形式，将F_0移出积分式：

$$=\int_{2\pi} \frac{fr}{F}Fcos(N,in)d\omega$$

$$=\int_{2\pi} \frac{fr}{F}(F_0 + (1-F_0)*p)cos(N,in)d\omega$$

$$=\int_{2\pi} \frac{fr}{F}(F_0*(1-p) + p)cos(N,in)d\omega$$

$$=\int_{2\pi} \frac{fr}{F}(F_0*(1-p))cos(N,in)d\omega + \int_{2\pi} \frac{fr}{F}p*cos(N,in)d\omega$$

$$=\int_{2\pi} \frac{fr}{F}(F_0*(1-(1- \omega_o · h)^5))cos(N,in)d\omega + \int_{2\pi} \frac{fr}{F}(1- \omega_o · h)^5)*cos(N,in)d\omega$$

$$=F_0*\int_{2\pi} \frac{fr}{F}((1-(1- \omega_o · h)^5))cos(N,in)d\omega + \int_{2\pi} \frac{fr}{F}(1- \omega_o · h)^5)*cos(N,in)d\omega$$

这里我们成功把DFG项写成了这样的形式：

$$= F_0 * a + b$$

所以我们预处理的时候，只需要针对每一个n · w_o和粗糙度的取值，计算出一个a和b的结果即可，这样在pbr着色器中直接根据n · w_o和粗糙度的取值，得到a和b，那么积分的估计值就是F_0*a+b。

所以我们不妨将预处理结果写入一张纹理中，我们称之为Lut纹理，其中x轴表示n · w_o，y轴表示粗糙度，像素的r通道储存a值，像素的g通道储存b值。

首先我们来绑定一下Lut纹理：

/*Lut预计算*/
    unsigned int brdfLUTTexture;
    glGenTextures(1, &brdfLUTTexture);

    glBindTexture(GL_TEXTURE_2D, brdfLUTTexture);
    glTexImage2D(GL_TEXTURE_2D, 0, GL_RG16F, 512, 512, 0, GL_RG, GL_FLOAT, 0);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
    glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
    glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
    glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512);
    glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, brdfLUTTexture, 0);

    glViewport(0, 0, 512, 512);
    shader_lut.use();
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    glBindVertexArray(quadVAO);
    glDrawArrays(GL_TRIANGLES, 0, 6);

    glBindFramebuffer(GL_FRAMEBUFFER, 0);

然后我们定义一下lut的片元着色器写法，基本上是继承了mipmap那个着色器的内容：

#version 330 core
out vec4 FragColor;
in vec2 TexCoords;

const float PI = 3.14159265359;

float RadicalInverse_VdC(uint bits)
vec2 Hammersley(uint i, uint N)
vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)

float GeometrySchlickGGX(float NdotV, float roughness)
{
    float a = roughness;
    float k = (a * a) / 2.0;

    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return nom / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2 = GeometrySchlickGGX(NdotV, roughness);
    float ggx1 = GeometrySchlickGGX(NdotL, roughness);

    return ggx1 * ggx2;
}

vec2 IntegrateBRDF(float NdotV, float roughness)
{
    vec3 V;
    V.x = sqrt(1.0 - NdotV*NdotV);
    V.y = 0.0;
    V.z = NdotV;

    float A = 0.0;
    float B = 0.0;

    vec3 N = vec3(0.0, 0.0, 1.0);

    const uint SAMPLE_COUNT = 1024u;
    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
    {
        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
        vec3 H  = ImportanceSampleGGX(Xi, N, roughness);
        vec3 L  = normalize(2.0 * dot(V, H) * H - V);

        float NdotL = max(L.z, 0.0);
        float NdotH = max(H.z, 0.0);
        float VdotH = max(dot(V, H), 0.0);

        if(NdotL > 0.0)
        {
            float G = GeometrySmith(N, V, L, roughness);
            float G_Vis = (G * VdotH) / (NdotH * NdotV);
            float Fc = pow(1.0 - VdotH, 5.0);

            A += (1.0 - Fc) * G_Vis;
            B += Fc * G_Vis;
        }
    }
    A /= float(SAMPLE_COUNT);
    B /= float(SAMPLE_COUNT);
    return vec2(A, B);
}
// ----------------------------------------------------------------------------
void main() 
{
    vec2 integratedBRDF = IntegrateBRDF(TexCoords.x, TexCoords.y);
    FragColor = vec4(integratedBRDF,0,1);
}

注意我们依然要使用重要性采样！所以很多函数和前面的hdr_mipmap的着色器是重合的。最后我们可以获取到Lut纹理的结果：

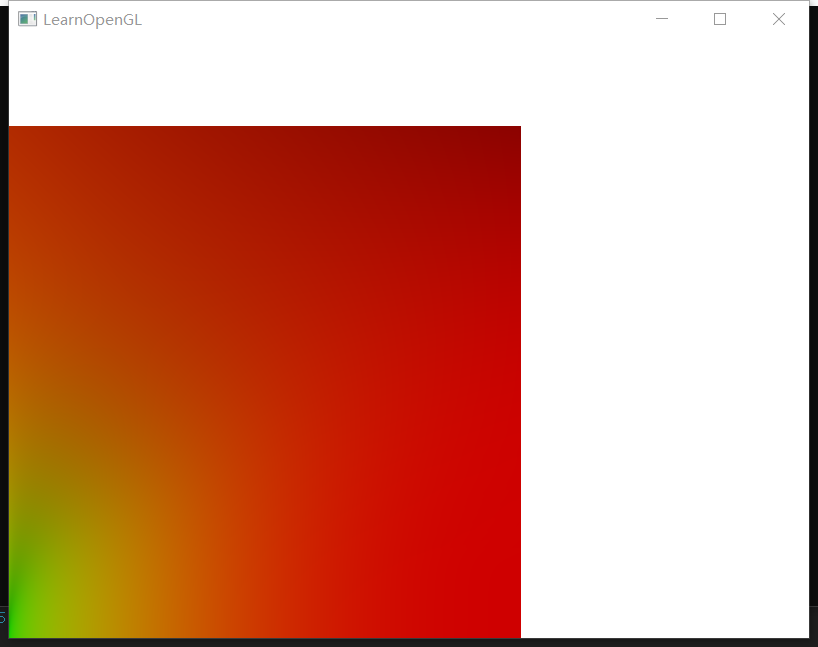
由于我做了一点后处理的内容，所以颜色可能稍微有点偏差，不过Lut结果应该是准确的。

3、积分整合

现在我们把光源积分部分和DFG积分部分的值都预处理好了，那么我们就可以整合环境光对镜面反射部分的贡献了：

vec3 R = reflect(-V, N);
    vec3 prefilteredColor = textureLod(reflect_mipmap, R,  roughness_ * 4).rgb;
    vec2 envBRDF  = texture(reflect_lut, vec2(max(dot(N, V), 0.0), roughness_)).rg;
    vec3 environment_reflect = prefilteredColor * (F0 * envBRDF.x + envBRDF.y);
    FragColor.rgb += ambient_ * (environment_diffuse + environment_reflect);
    FragColor.a = diffuse_.a;

首先R是视线方向的镜面反射向量，用这个向量去采样mipmap（mipmap的分级由粗糙度决定），得到光源积分的结果L；同时计算出当前的n · v和粗糙度并在Lut纹理中查表，得到a和b的值，最后镜面反射的光照贡献结果就是：

$$L * (F_0 * a + b)$$

最后我们终于得到了 漫反射项和镜面反射项都受到环境光照贡献的结果：

哭辽，终于把learnOpengl啃完辽~

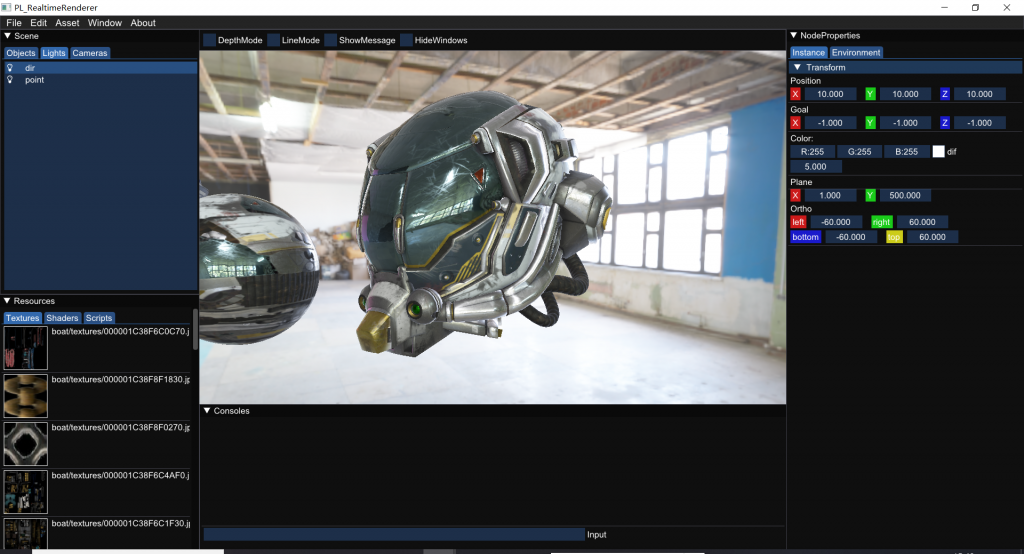
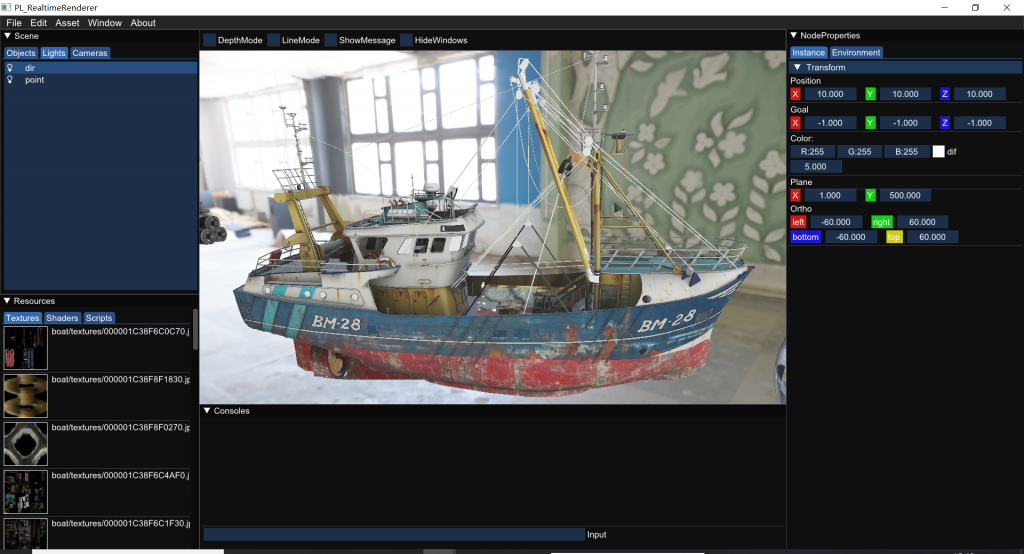
然后我用imgui做了个简单的界面：