引言

上一节我们完成了光照、材质、模型的导入，已经拥有了一个场景的雏形。这节我们来深入讨论一下测试、混合、高级数据和着色器相关的内容。

Part1. 深度测试

靠前的物体能够挡住靠后的物体，本质原因是靠前的物体深度值更小，而靠后的物体深度值更大，我们默认用深度值小的像素去替换掉深度值大的像素，这样就完成了遮挡关系的判断。当然，是否要取深度值小的、抛弃深度值大的，其实也可以交给用户自定义，通过glDepthFunc()方法可以修改逻辑：GL_ALWAYS永远通过测试、GL_LESS最常用的浅值通过测试、GL_GREATER深值通过测试；

同时，由于投影变换的缘故，导致在屏幕空间下，所有物体的像素深度与相机空间下的真实深度距离之间不再是线性关系，这是因为投影变换将z值做了一个压缩。所以如果我们想得到相机空间下的真实深度，只能通过屏幕空间下的深度值先做一个“逆NDC转换”，再做一个“逆投影变换”。

我们先看一下正投影变换的变换矩阵：

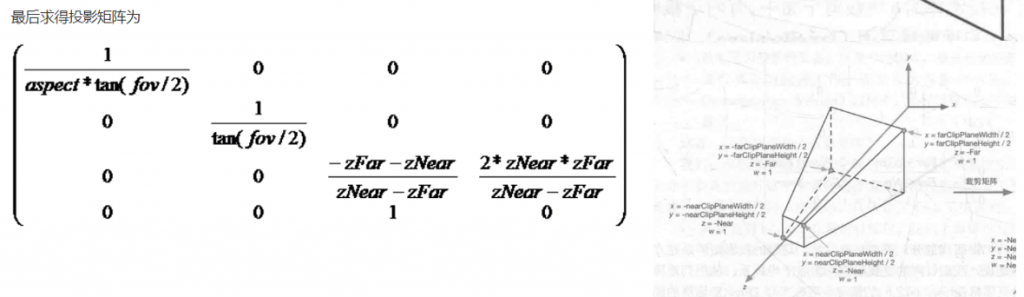
假设相机空间下的空间坐标是(x,y,z,w)，投影变换后的空间坐标是(x’,y’,z’,w’)，NDC空间下的空间坐标是(x_NDC,y_NDC,z_NDC,w_NDC)，而屏幕空间下的深度为depth，则有：

$$z’ = z * \frac{far + near}{far-near} + w * \frac{2 * near * far}{near – far}$$

$$z_{NDC} = \frac{z’}{-z}$$

$$depth = \frac{z_{NDC} + 1}{2}$$

可以反推：

$$z_{NDC} = \frac{far + near}{near – far} – \frac{2 * near * far}{z * (near – far)}$$

$$\frac{2 * near * far}{z * (near – far)} = \frac{far + near}{near – far} – z_{NDC}$$

$$z = \frac{2 * near * far}{far + near – z_{NDC} * (far – near)}$$

这样z、z_NDC和depth之间的关系我们就捋清楚了，z就是真实线性深度，depth是屏幕空间的非线性深度，之间做个转换即可：

#version 330 core
out vec4 FragColor;
float near = 0.1; 
float far  = 100.0; 
float LinearizeDepth(float depth) 
{
    float z = depth * 2.0 - 1.0;
    return (2.0 * near * far) / (far + near - z * (far - near));
}
void main()
{             
    float depth = LinearizeDepth(gl_FragCoord.z) / far;
    FragColor = vec4(vec3(depth), 1.0);
}

这样就能显示线性的深度信息了：

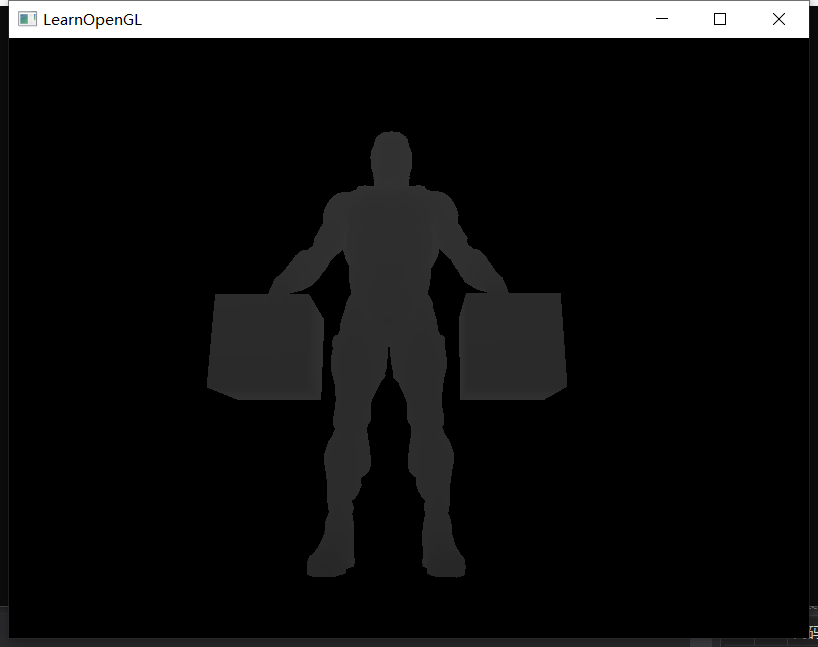
最后就是要尽量防止深度冲突，即不同物体的两个片元不仅处于屏幕中的同一像素处，还处于完全相同的深度值，这样opengl无法判断该绘制哪一个。避免深度冲突的方法有三种：1、不同物体之间不要贴太死；2、将近视裁剪平面放远一点，加大近距离物体的深度数值精度；3、使用更高精度的深度缓冲。

Part2. 模板测试

模板测试和深度测试本质是很相似的，都是对每一个像素产生一个属性值，然后根据该属性值决定是否要丢弃该片元。只是如何设置模板值、模板测试通过条件、通过和不通过后的事件需要我们自己来定义。

首先要介绍的一个接口是glStencilFunc(GLenum func, GLint ref, GLuint mask)，第一个参数定义模板的测试通过条件，第二个参数定义对比测试的参考值，第三个参数定义掩码，通过与运算将要做测试的位取出来。

另一个很重要的接口是glStencilOp(GLenum sfail, GLenum dpfail, GLenum dppass)，主要设置当模板测试通过或未通过后，要采取的行为是什么。第一个参数定义模板测试失败后的行为；第二个参数定义模板测试通过但深度测试失败的行为；第三个参数定义模板测试和深度测试都通过的行为。默认取值是GL_KEEP，表示不采取任何行为。

下面是一个描边效果的模板测试案例：

glEnable(GL_DEPTH_TEST);
glStencilOp(GL_KEEP, GL_KEEP, GL_REPLACE);  

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT | GL_STENCIL_BUFFER_BIT); 

glStencilMask(0x00);
normalShader.use();
DrawFloor()  

glStencilFunc(GL_ALWAYS, 1, 0xFF); 
glStencilMask(0xFF); 
DrawTwoContainers();

glStencilFunc(GL_NOTEQUAL, 1, 0xFF);
glStencilMask(0x00); 
glDisable(GL_DEPTH_TEST);
shaderSingleColor.use(); 
DrawTwoScaledUpContainers();
glStencilMask(0xFF);
glEnable(GL_DEPTH_TEST); 

思路就是：首先定义模板测试后的行为：若模板测试或深度测试失败就保持模板值+丢弃片元，若测试成功则用对比参考值来覆盖原本的模板值。等到开始画箱子的时候，使用GL_ALWAYS表示恒测试成功，那么这时候所有片元所在的像素模板值都会覆盖成参考值1；接下来将箱子放大，将模板测试的条件改为不等于1，可以预见只有放大后比原本箱子扩展出来的边缘部分模板值不是1，可以通过测试，那么这部分我们使用新的shader来对这部分片元进行描边。

所以模板测试本质上，就是让某个先渲染的物体在缓冲中留下标记，然后渲染后面的物体的时候，可以根据标记做一些特殊的效果。

（因为这部分对于我们最终的渲染器意义不大，复现完还得删，因此就不复现功能了）

Part3. 透明混合

之前我们读取的纹理都是RGB三通道的，没有最后一个A通道，因此是完全不透明的。但是有时候，我们希望能引入半透明度通道，从而实现物体表面的半透效果。首先我们修改纹理读取函数：

glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data);

然后将materal中的diffuse分量改成vec4类型，附加上a通道。首先我们考虑一种极端情况：完全透明，这时候diffuse的a通道值为0，此时我们可以直接将该片元剔除：

vec4 rho_d;
    if(material.diffuse_texture_use == true) rho_d = vec3(texture(material.diffuse_texture, texcoord));
    else rho_d = material.diffuse;
    if(rho_d.a <= 0.1)
        discard;

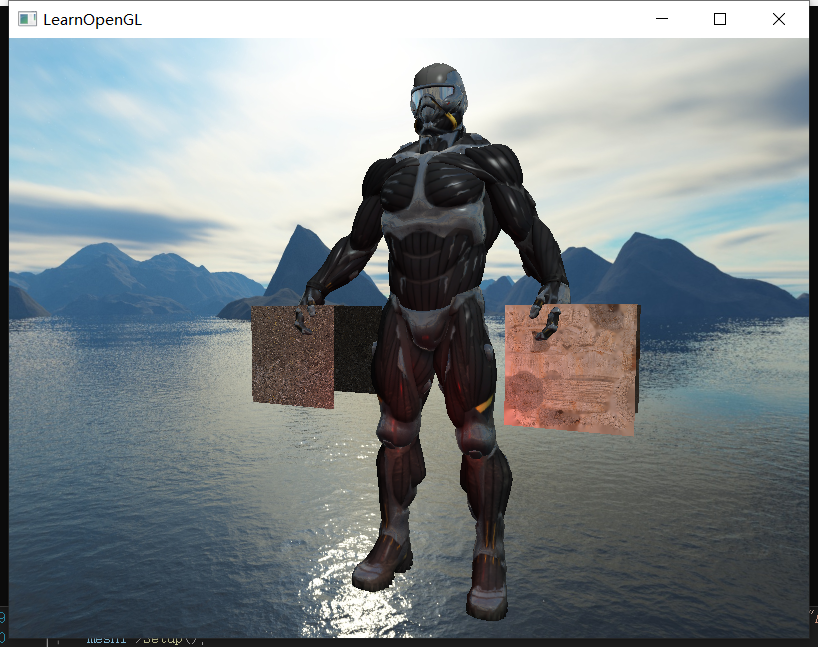
事实上我们的角色贴图确实带有很多半透区域：

所以加入透明通道判断后，就会有很多区域出现透明了：

接下来考虑一下普遍的情况：有半透明，但不完全透明。这种情况下，需要保留一部分片元的颜色，还要获得被该片元遮挡的片元的颜色，最后要对两者进行一个混合。如何进行“混合”是解决半透明渲染的精髓所在，因此opengl也提供了若干个混合相关的接口。

首先是glEnable(GL_BLEND)开启混合功能。与模板测试类似，混合测试也提供了glBlendFunc、glBlendEquation等可以自定义混合条件的接口。glBlendFunc(GLenum sfactor, GLenum dfactor)是导入混合因子的接口，其中sfactor是当前片元的着色比例，dfactor是颜色缓冲中已经写入的颜色的着色比例。一般来说，我们让sfactor=当前片元着色结果的a通道值；dfactor=1-sfactor即可，具体写法就是glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)。例如片元的a值=0.3，那么最终该像素的着色结果就=0.3*片元着色值+0.7*颜色缓冲值。

另一个接口是glBlendEquation(GLenum mode)，它定义的了片元着色和缓冲区颜色之间应该按比例相加还是相减，如果是相减那么是谁减谁，一般情况我们都只使用相加。

所以实际上要添加的代码非常简单：

    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

然后我们便可以看到半透明混合的结果了：

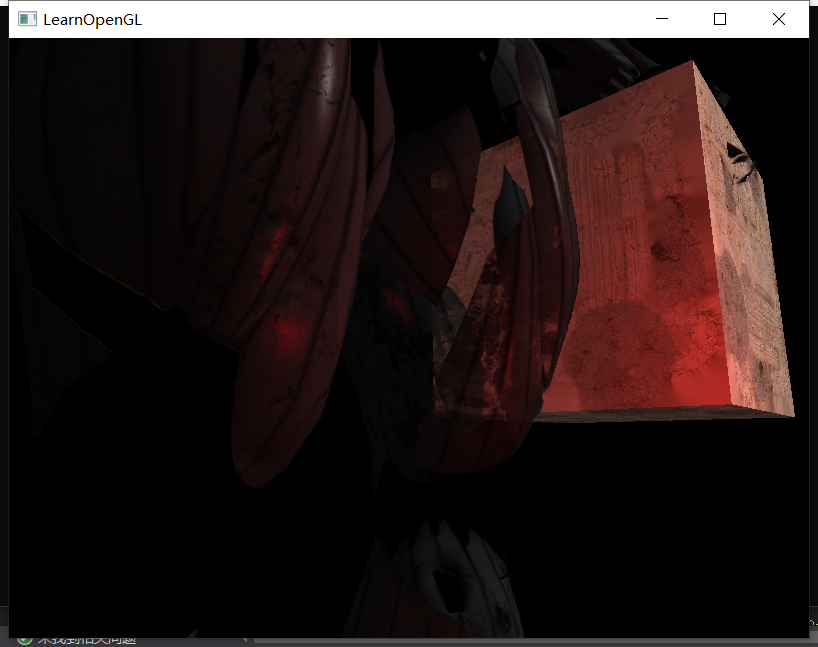
但是这里还埋着一个坑，考虑这样一个情况：A半透、较近，B半透、较远，由于我们开启了深度测试，当我们优先渲染A时，便会在深度缓冲中留下A的深度信息，而此时判断B时，直接通不过深度测试就被丢弃了，最后就没能把B的颜色信息写入。

有人会说，那我们可以拒绝写入半透明物体的深度信息啊，这样做倒是可以解决误丢片元这个问题，然而事实上还存在另一个问题。对于上述场景，正确的混合结果应该是：

$$C = a_A * rgb_A + (1 – a_A) * (a_B * rgb_B + (1 – a_B) * rgb_{background})$$

然而如果我们优先渲染A，那我们实际的计算就会变成：

$$C = a_B * rgb_B + (1 – a_B) * (a_A * rgb_A + (1 – a_A) * rgb_{background})$$

显然结果就不对了。这个事情告诉我们：对于多个半透明物体，渲染顺序是非常重要的，我们要从最深最远的半透明物体开始渲染，不断逐步更新颜色缓冲，最后才能得到正确的结果。因此，在渲染场景前，需要先对所有半透明物体根据距离排序，然后从距离最大的开始渲染。

教程中使用map来存储各个半透明物体的距离，然后实现排序：

std::map<float, glm::vec3> sorted;
for (unsigned int i = 0; i < windows.size(); i++)
{
    float distance = glm::length(camera.Position - windows[i]);
    sorted[distance] = windows[i];
}
...
for(std::map<float,glm::vec3>::reverse_iterator it = sorted.rbegin(); it != sorted.rend(); ++it) 
{
    model = glm::mat4();
    model = glm::translate(model, it->second);              
    shader.setMat4("model", model);
    glDrawArrays(GL_TRIANGLES, 0, 6);
}

但是排序的前提是要获得距离，也就是说我们要给场景中每个物体定义一个“中心点”，将中心点到相机的距离作为“物体”的距离，然后再用map进行排序。当然，很快这样就又产生新的问题了：

上图的三个物体就没有一个明确的深度顺序，某种意义上他们的深度也是一样的，此时排序算法就不再有效了。

Part4. 面剔除

当我们做一个模型的时候，其实有一个通用的规则，就是对于正面朝外的三角形，从外面看 三个点的顺序要么都是顺时针，要么都是逆时针。假如导出模型的时候，所有正面朝外的面的顶点都是顺时针，那么当着色器处理三角形时，发现从当前视角看 其三个顶点是逆时针的，说明这个面没有面朝自己，我们就预设它是“不可能被看到的面”，从而尽早丢弃掉。

事实上在一个场景中，若所有物体都是封闭的，那么至少有一半的面都是背对自己的，如果能尽早剔除它们，就可以省下一般的算力。

开启面剔除的接口是glEnable(GL_CULL_FACE)，同时我们要用glFrontFace()指定正面的顶点应该是顺时针还是逆时针（默认是GL_CCW逆时针，而GL_CW是顺时针），并用glCullFace(GL_BACK/GL_FRONT)指定要剔除的是背面还是正面。

    glEnable(GL_CULL_FACE);
    glCullFace(GL_BACK);
    glFrontFace(GL_CCW);

最后我得到了这样的结果：

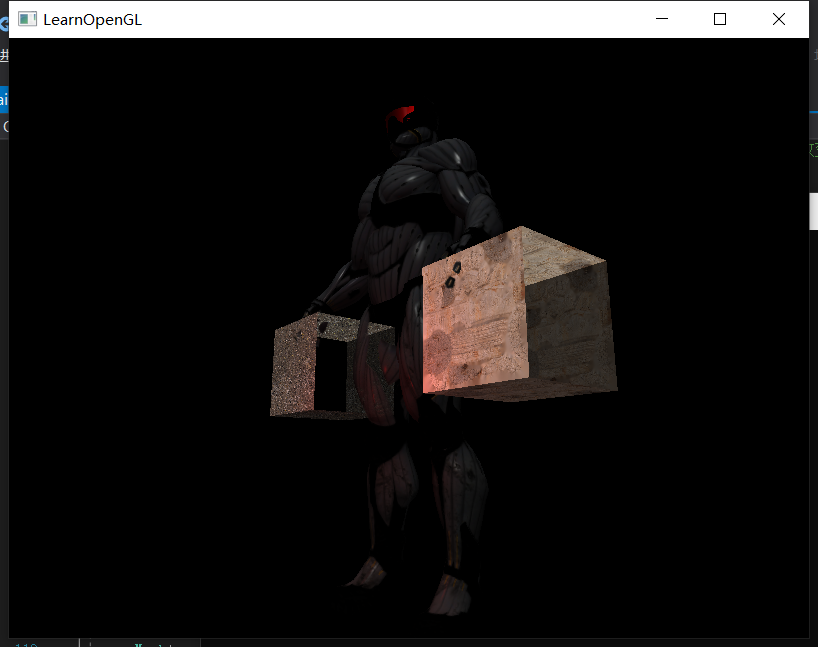
这也侧面反映了一件事：我做的正方体没有严格按照“对于正面朝外的三角形，从外面看 三个点的顺序要么都是顺时针，要么都是逆时针”的规则来，所以最后就是有些不该剔除的面被剔除，有些该剔除的面没被剔除……不过没关系，后面我基本上只会导入外部模型，不会徒手搓模型信息了。对于外部由建模软件生成的模型基本都会遵守上述的规则。

Part5. 帧缓冲

在前面几节介绍了颜色缓冲、深度缓冲、模板缓冲，如果我们将三者结合在一起，就变成了帧缓冲。下面简单说一下帧缓冲的工作机制：

首先opengl绑定了一个默认的帧缓冲，这里会不断地写入每一个像素的颜色、深度、模板值，等这些内容全部写完后，会将其全部转化到渲染缓冲（render buffer）中。渲染缓冲是高度原生化的数据，可以直接被opengl所用，这部分将直接被用于渲染画面、储存深度和模板值（方便下一回渲染时使用这些数据）。所以简而言之，就是在计算像素的各种缓冲信息时，先将所有结果写入默认帧缓冲中，待整个画面的缓冲信息都计算完了，就送至渲染缓冲进行数据应用。

但是有时候，我们希望对帧缓冲中得到的图像进行后期处理（饱和、亮度、模糊操作等），等后期处理完了再送到渲染缓冲进行绘制。这意味着我们需要取缔默认的帧缓冲，定制一个自己的帧缓冲去接收场景的图像，并将结果变成纹理形式；然后将这张纹理放到后处理的shader中进行处理，并将最终的纹理渲染到画面中。

所以流程简而言之就是：

定义自己的帧缓冲-将自定义帧缓冲绑定-用普通shader渲染图像到帧缓冲-将自定义帧缓冲结果写入纹理-绑定回默认帧缓冲-用后处理shader处理纹理并输出到默认帧缓冲，它会自动地送至渲染缓冲去渲染。

但是这里还有一点细节可以优化，那就是：我们只需要对颜色缓冲进行后处理，并不需要对深度信息、模板信息进行处理，所以当我们将所有缓冲结果写入到自定义的帧缓冲后，我们可以从帧缓冲中提取出深度信息和模板信息直接写入渲染缓冲。

帧缓冲、缓冲纹理、渲染缓冲绑定：

unsigned int framebuffer;
    glGenFramebuffers(1, &framebuffer);
    glBindFramebuffer(GL_FRAMEBUFFER, framebuffer);

    unsigned int textureColorbuffer;
    glGenTextures(1, &textureColorbuffer);
    glBindTexture(GL_TEXTURE_2D, textureColorbuffer);
    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, screenWidth, screenHeight, 0, GL_RGB, GL_UNSIGNED_BYTE, NULL);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
    glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, textureColorbuffer, 0);

    unsigned int rbo;
    glGenRenderbuffers(1, &rbo);
    glBindRenderbuffer(GL_RENDERBUFFER, rbo);
    glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH24_STENCIL8, screenWidth, screenHeight); // use a single renderbuffer object for both a depth AND stencil buffer.
    glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_STENCIL_ATTACHMENT, GL_RENDERBUFFER, rbo); // now actually attach it

绑定部分主要分了三部分，第一步我们定义一下自己的帧缓冲，然后将其绑定到GL_FRAMEBUFFER上，从而接收管线中得到的缓冲结果；第二步我们定义并绑定缓冲纹理textureColorbuffer，将帧缓冲的颜色部分写入到我们的textureColorbuffer中，这样我们的后处理shader在这个纹理上采样即可；第三步我们定义渲染缓冲，将我们帧缓冲的深度、模板部分直接写入到渲染缓冲中。

现在我们拿到了渲染结果的颜色纹理了，但是如果想用shader处理这个纹理，必须先将纹理贴到模型上（没有模型的话，顶点和片元的概念也就都没有了），我们直接定义一个长方形模型，由两个三角形组成：

float quadVertices[] = {
        -1.0f,  1.0f,  0.0f, 1.0f,
        -1.0f, -1.0f,  0.0f, 0.0f,
         1.0f, -1.0f,  1.0f, 0.0f,

        -1.0f,  1.0f,  0.0f, 1.0f,
         1.0f, -1.0f,  1.0f, 0.0f,
         1.0f,  1.0f,  1.0f, 1.0f
};
...
/*屏幕的纹理模型设置*/
    unsigned int quadVAO, quadVBO;
    glGenVertexArrays(1, &quadVAO);
    glGenBuffers(1, &quadVBO);
    glBindVertexArray(quadVAO);
    glBindBuffer(GL_ARRAY_BUFFER, quadVBO);
    glBufferData(GL_ARRAY_BUFFER, sizeof(quadVertices), &quadVertices, GL_STATIC_DRAW);
    glEnableVertexAttribArray(0);
    glVertexAttribPointer(0, 2, GL_FLOAT, GL_FALSE, 4 * sizeof(float), (void*)0);
    glEnableVertexAttribArray(1);
    glVertexAttribPointer(1, 2, GL_FLOAT, GL_FALSE, 4 * sizeof(float), (void*)(2 * sizeof(float)));

现在我们要送入到另一套shader中：postprocess shader，来对这个纹理进行颜色后处理，并将其输出到屏幕的对应像素上，那么着色器可以这样写：

//////////////////////////vertex shader//////////////////////////
#version 330 core
layout (location = 0) in vec2 aPos;
layout (location = 1) in vec2 aTexCoords;

out vec2 TexCoords;

void main()
{
    gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0); 
    TexCoords = aTexCoords;
}

//////////////////////////fragment shader//////////////////////////
#version 330 core
out vec4 FragColor;

in vec2 TexCoords;
uniform sampler2D screenTexture;

void main()
{ 
    vec4 colors = texture(screenTexture, TexCoords);
    //这里对colors进行后处理
    FragColor = colors;
}

然后我们在渲染循环中，将纹理喂到这个shader中：

        glBindFramebuffer(GL_FRAMEBUFFER, framebuffer);
        glEnable(GL_DEPTH_TEST);

        glClearColor(0.0f, 0.0f, 0.0f, 1.0f); 
...
        mesh1->Draw(shader);
        mesh2->Draw(shader);
        models->Draw(shader);

        glBindFramebuffer(GL_FRAMEBUFFER, 0);
        glDisable(GL_DEPTH_TEST);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
        glClear(GL_COLOR_BUFFER_BIT);

        shader_post.use();
        glBindVertexArray(quadVAO);
        glBindTexture(GL_TEXTURE_2D, textureColorbuffer);
        glDrawArrays(GL_TRIANGLES, 0, 6);

        glfwSwapBuffers(window);
        glfwPollEvents();     

注意，当进入到后处理阶段的时候，要关闭深度测试，防止深度测试把纹理模型的顶点或片元吞掉。

现在，我们就可以对纹理进行调整，并将调整后的结果渲染到屏幕上了。不过具体怎么调整的代码还没写，可以添加一些修改饱和度、亮度的方法，也可以做高斯模糊、拉普拉斯滤波、边缘检测，这部分能做的事非常自由，就不具体写了。

Part6. 立方体贴图

目前的环境全部是纯色，现在我们要第一次引入环境贴图的概念。不过与之前介绍的环境贴图不同，这次使用的是立方体形状的贴图。立方体一共包含6个平面，这也意味着我们要使用的贴图是由正方体展开后的6个正方形纹理组成。

现在我们来生成cubemap的纹理并绑定：

/*cubemap设置*/
    vector<std::string> faces
    {
        "D:/cg_opengl/OpenglRenderer/resources/cubemap/right.jpg",
        "D:/cg_opengl/OpenglRenderer/resources/cubemap/left.jpg",
        "D:/cg_opengl/OpenglRenderer/resources/cubemap/top.jpg",
        "D:/cg_opengl/OpenglRenderer/resources/cubemap/bottom.jpg",
        "D:/cg_opengl/OpenglRenderer/resources/cubemap/front.jpg",
        "D:/cg_opengl/OpenglRenderer/resources/cubemap/back.jpg"
    };
    unsigned int cubemapTexture = loadCubemap(faces);

...
unsigned int loadCubemap(vector<std::string> faces)
{
    unsigned int textureID;
    glGenTextures(1, &textureID);
    glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);

    int width, height, nrChannels;
    for (unsigned int i = 0; i < faces.size(); i++)
    {
        unsigned char* data = stbi_load(faces[i].c_str(), &width, &height, &nrChannels, 0);
        if (data)
        {
            glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i,
                0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data
            );
            stbi_image_free(data);
        }
        else
        {
            std::cout << "Cubemap texture failed to load at path: " << faces[i] << std::endl;
            stbi_image_free(data);
        }
    }
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);

    return textureID;
}

这里我们将6张图的路径放在一起，送入到自定义的loadCubemap函数中。此时我们要绑定的不再是普通的纹理了，而是GL_TEXTURE_CUBE_MAP。我们分别按照右、左、上、下、前、后的顺序读入6张纹理，分别载入到GL_TEXTURE_CUBE_MAP_POSITIVE_X + i中，即可将6张图完整地绑定在一张cubemap上。

现在我们获得了cubemap的纹理id，接下来要考虑的事情就是如何将他渲染在屏幕上。我们知道“环境”这个东西没有顶点，更无片元的概念，着色器并不好处理它。因此可以曲线救国：创建一个环境立方体，当其他所有物体全部渲染完毕后，我们这样渲染天空盒：

首先将相机的位置强行置0来推演view矩阵（因为环境立方体始终处于原点，将相机也置为原点就能保证它永远处于环境立方体的正中央）；然后在顶点着色器中，我们将投影变换后得到的坐标的w值替代z值（在顶点着色器之后，管线会将输出的gl_Position的xyz都除以w，最后得到的新z就是深度值。如果我们提前将gl_Position的z置为w的值，那么最后除以w得到的深度就恒为1.0。1.0这个深度值代表着最深处，这样就可以被任意物体都遮挡住了。）

这两个trick还是非常绝妙的，能这么乱玩trick的核心原因是我们提前把所有要绘制的物体都渲染完了，最后就剩下这么个环境立方体，所以才可以“乱动”相机、“乱写”gl_Position这些内容。

//////////////////////////vertex shader//////////////////////////
#version 330 core
layout (location = 0) in vec3 aPos;

out vec3 pos;

uniform mat4 model;
uniform mat4 view;

void main()
{
    pos = aPos;
    vec4 p = projection * view * vec4(aPos, 1.0);
    gl_Position = p.xyww;
}

//////////////////////////fragment shader//////////////////////////
#version 330 core
out vec4 FragColor;
in vec3 pos;

uniform samplerCube cubeTexture;

void main()
{ 
    FragColor = texture(cubeTexture, pos);
}

编写完shader后，我们便可以对环境立方体进行渲染了：

glDepthFunc(GL_LEQUAL);
        shader_cubemap.setInt("cubeTexture", 0);
        view = glm::mat4(glm::mat3(camera->getView()));
        shader_cubemap.setMatrix("view", view);
        shader_cubemap.setMatrix("projection", projection);
        shader_cubemap.use();
        glActiveTexture(GL_TEXTURE0);
        glBindTexture(GL_TEXTURE_CUBE_MAP, cubemapTexture);
        glBindVertexArray(skyboxVAO);
        glDrawArrays(GL_TRIANGLES, 0, 36);

首先深度缓冲的默认值是1.0，而我们环境立方体的深度值也是1.0，如果深度缓冲条件是LESS的话那么立方体永远通过不了深度测试，所以必须改成GL_LEQUAL。然后我们将相机的view矩阵改成3*3的形式，这其实就是剔除相机的世界坐标（等价于将相机移至(0,0,0)）；最后我们绑定立方体贴图并进行渲染。

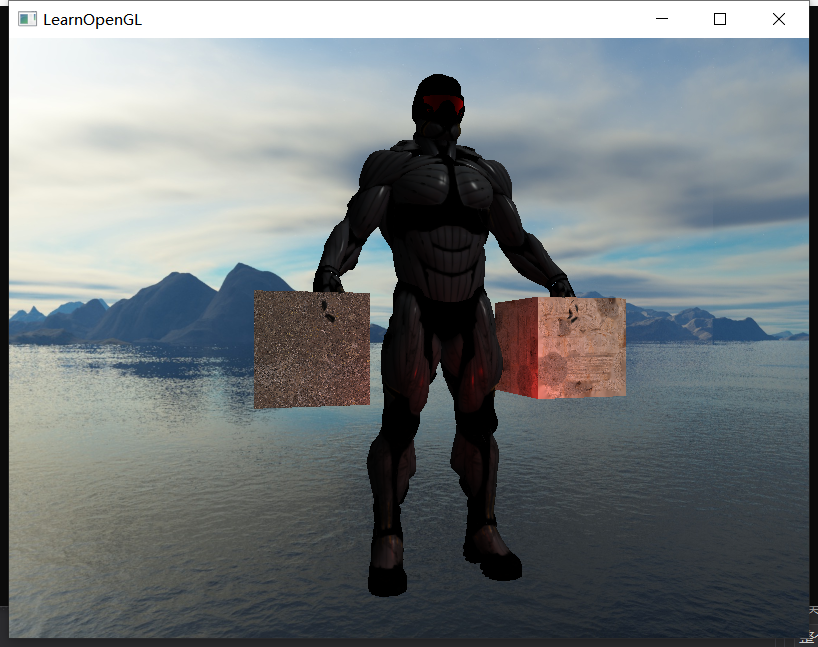
接下来learnOpengl玩了个花活，一个是材质反射环境贴图，一个是材质透射环境贴图。对于前者做起来还有那么点意义；至于后者，又不考虑菲涅尔，又不考虑全内反射，而且只有入射没有出射，与真正透射的差距实在太大，就不复现了。

那么我们来看一下反射，反射本质上就是将反射方向上的环境贴图着色与漫反射颜色做一个混合，当反射分量为1的时候，模型表面只有环境贴图的颜色；当反射份量为0的时候，模型表面全部是漫反射和高光分量。

具体思路比较清晰，首先我们要将环境贴图传入模型渲染的shader中，然后在片元着色器中根据视角向量和模型法线确定反射方向，然后按照反射方向对环境贴图进行采样即可。这里我们添加一个reflect参数和reflect贴图，用来控制反射率。（这里有一个大坑，就是官方给的模型里附带了反射贴图，但是它会被识别成ambient texture）

最后可以得到如下的反射图样：

至于透射就不做了，但凡做过光追的透射，就知道实时渲染的这个透射有多离谱了，做的意义不太大。

Part7. 高级数据

这一节主要是概念讲述，没有具体要实现的需求。这里介绍了一些比较好用的api：

glBufferData，给某个缓冲内存区分配内存，并填充一段数据；

glBufferSubData，向某个缓冲内存区的特定区域填充一段数据（调用这个之前要先调用glBufferData来分配内存）；

glMapBuffer，返回某个已绑定缓冲区的内存指针；

glUnmapBuffer，将glMapBuffer所得到的指针无效化；

glCopyBufferSubData，复制某一个已绑定缓冲区的数据 到 另一个已绑定缓冲区中。

这一节就是介绍了这些对缓冲区进行初始化、赋值、复制粘贴的一些相关api。

Part8. 高级GLSL

这节主要深入探讨了一些shader中的拓展知识和技巧。

首先讲了内建变量，除了我们常用的gl_FragPosition（透视投影后的顶点坐标）和FragColor（片元颜色结果）外，还有一些可以用的内建变量：

gl_PointSize：每个图元的像素大小，默认为1；

gl_VertexID：顶点着色器中当前顶点的id号；

gl_FragCoord：屏幕空间坐标，x、y是该片元在屏幕上的横、纵坐标，z是深度值（非线性）；

gl_FrontFacing：当前片元所处的三角面是否正面朝向相机；

gl_FragDepth：修改片元的深度值；

然后讲了一个不太重要的概念：Uniform缓冲。因为我们在场景中会用到很多不同的shader，但是这些shader有一些输入量是完全一样的，例如model矩阵、view矩阵和projection矩阵，那么我们就可以定义一个uniform缓冲，将所有shader的这些uniform变量全部设置好。具体绑定方式比较复杂，而且目前没有使用它的需求。

Part9. 几何着色器

这一节相对就比较重要了。几何着色器是一个介于顶点着色器和片元着色器之间的着色器，它的输入是一个图元的一组顶点，输出可以是0个甚至多个不同的图元。

回忆我们管线的流程，在顶点着色器后，管线会对顶点进行三角形图元的组织，计算出哪些顶点构成了一个三角形、对应的三角形内部有哪些片元。几何着色器对应的就是这一步，当我们组织成一个三角形的时候，我们可以用几何着色器对组织结果进行介入修改，最后返还修改过的三角形片元再交给片元着色器。

举一个官方的例子，原本图上只有4个顶点：

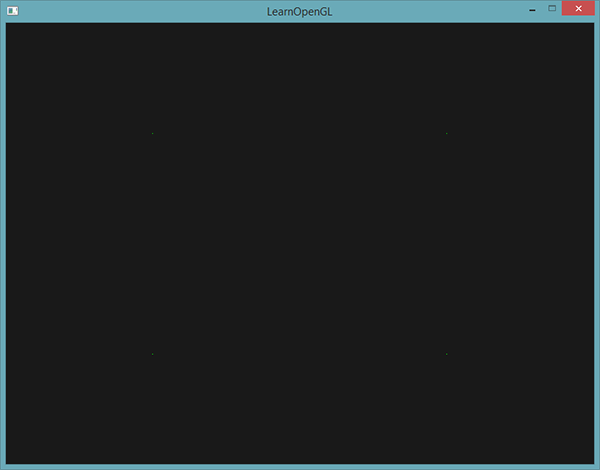
我们如下编辑几何着色器：

#version 330 core
layout (points) in;
layout (triangle_strip, max_vertices = 5) out;

void build_house(vec4 position)
{    
    gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0);    // 1:左下
    EmitVertex();   
    gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0);    // 2:右下
    EmitVertex();
    gl_Position = position + vec4(-0.2,  0.2, 0.0, 0.0);    // 3:左上
    EmitVertex();
    gl_Position = position + vec4( 0.2,  0.2, 0.0, 0.0);    // 4:右上
    EmitVertex();
    gl_Position = position + vec4( 0.0,  0.4, 0.0, 0.0);    // 5:顶部
    EmitVertex();
    EndPrimitive();
}

void main() {    
    build_house(gl_in[0].gl_Position);
}

相当于对于每一个顶点图元的输入，我们在其基础上创建新的顶点图元，并最后输出一个三角形带：

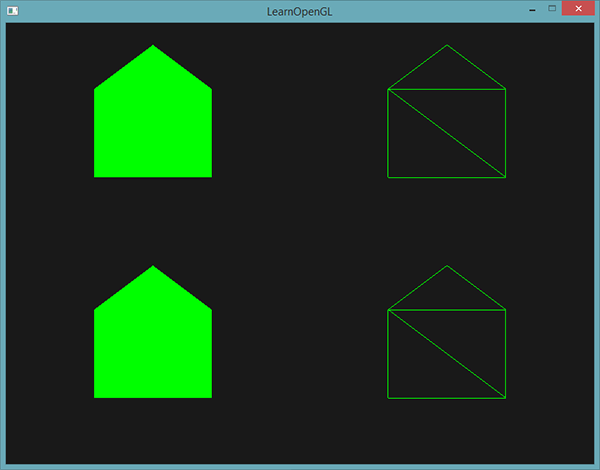
这里就展示了几何着色器的强大之处：可以修改甚至添加图元。接下来我们来实现一个效果，就是官方演示的爆破效果，即所有三角面都沿着法线平移一小段距离。

表面上这是一个很简单的“移动顶点”的案例，所以理论上在顶点着色器上就能做，但是假如我们没有输入“法线”这个uniform变量，那么在顶点着色器中，我们就无法获取其他顶点来计算法线。但是在几何着色器中就没有这个问题了，因为几何着色器的输入可以是三角形的三个点，根据三个点的坐标就可以计算出来法线的方向。

我们来编写一下这个“gsh”的几何着色器。在写它之前，我们先简单修改一下顶点着色器：

#version 330 core

layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aUV;
layout (location = 2) in vec3 aNormal;

out VS_OUT {
   vec3 normal;
   vec2 texcoord;
   vec3 FragPos;  
}vs_out;

uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

void main()
{
   gl_Position = projection * view * model * vec4(aPos, 1.0);
   vs_out.FragPos = vec3(model * vec4(aPos, 1.0));
   vs_out.normal = mat3(transpose(inverse(model))) * aNormal;;
   vs_out.texcoord = aUV;
}

这里主要是修改一下输出格式，将三个要输出的参数打包进VS_OUT块中；然后我们便可以编写几何着色器来接收传递这些参数：

#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices = 3) out;

in VS_OUT {
   vec3 normal;
   vec2 texcoord;
   vec3 FragPos;  
} gs_in[];

out vec3 f_normal;
out vec2 f_texcoord;
out vec3 f_FragPos; 

uniform float time;

vec4 explode(vec4 position, vec3 normal)
{
    return position;
    float magnitude = 2.0;
    vec3 direction = normal * ((sin(time) + 1.0) / 2.0) * magnitude; 
    return position + vec4(direction, 0.0);
}

vec3 GetNormal()
{
   vec3 a = vec3(gl_in[0].gl_Position) - vec3(gl_in[1].gl_Position);
   vec3 b = vec3(gl_in[2].gl_Position) - vec3(gl_in[1].gl_Position);
   return normalize(cross(a, b));
}

void main() {    
    vec3 normal = GetNormal();

    gl_Position = explode(gl_in[0].gl_Position, normal);
    f_normal = gs_in[0].normal;
    f_texcoord = gs_in[0].texcoord;
    f_FragPos = gs_in[0].FragPos;
    EmitVertex();
    gl_Position = explode(gl_in[1].gl_Position, normal);
    f_normal = gs_in[1].normal;
    f_texcoord = gs_in[1].texcoord;
    f_FragPos = gs_in[1].FragPos;
    EmitVertex();
    gl_Position = explode(gl_in[2].gl_Position, normal);
    f_normal = gs_in[2].normal;
    f_texcoord = gs_in[2].texcoord;
    f_FragPos = gs_in[2].FragPos;
    EmitVertex();
    EndPrimitive();
}

首先我们的输入是每个三角形的三个顶点，当我们拿到三个顶点时首先计算他们的法线方向，然后让三个顶点分别按照法线进行一小段距离的平移，平移的尺度随着uniform时间变化，最后将这三个顶点发射连成新的三角形。

在管线中，我们也要附加一个几何着色器的空间，将外部的几何着色器读入、编译并绑定。

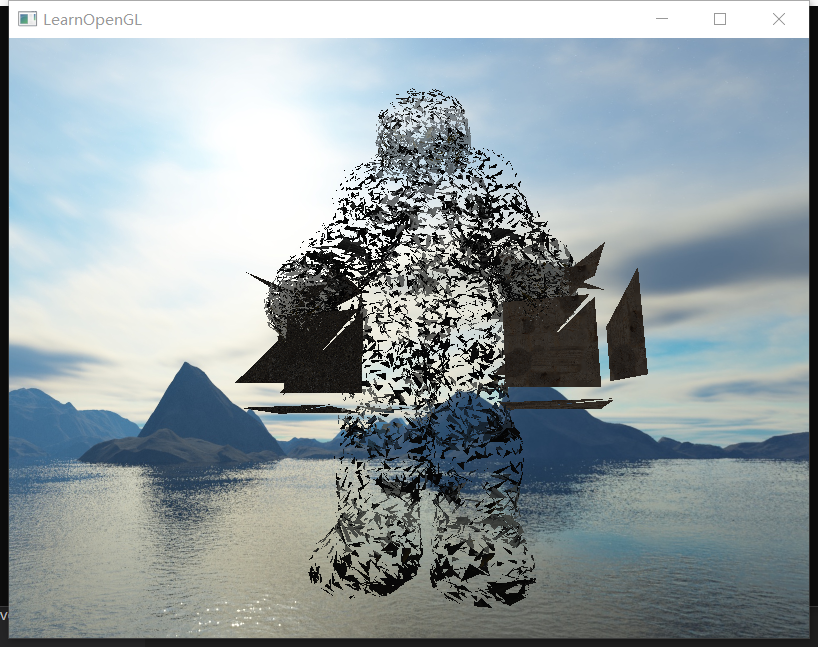
感觉还是蛮有意思的。相当于我们可以根据所有顶点图元、线图元或面图元，来进行增、删、改这些图元的各种属性，从而实现vs和fs所实现不了的几何效果。

Part10. 实例化

GPU处理大量数据的能力是非常强的，但是CPU却不是。如果我们有数以百万的顶点要交给GPU去渲染，那么CPU就会耗费大量性能 不断地将这些顶点送至GPU（这就是DrawCall）。

如果我们需要渲染的实例是高度重复的（例如行星周围一圈的碎屑，火焰的火苗粒子，落叶，草），那么我们可以只让CPU传送一个实例，然后直接告诉GPU要渲染多少次，那么传送任务就会简化非常多，需要消耗的draw call性能也会少很多。等后期我们做粒子系统的时候会复现这个内容。

Part11. 抗锯齿

锯齿是物体边缘出现的锯齿状走样现象，主要是因为屏幕的像素块太大，采样率过低，所以就会呈现一块一块的阶梯状。所以我们可以在光栅化阶段中对一个像素区域内使用多个子采样点，然后对着每个子采样点调用片元着色器计算着色并加和取平均，这个就是SSAA：

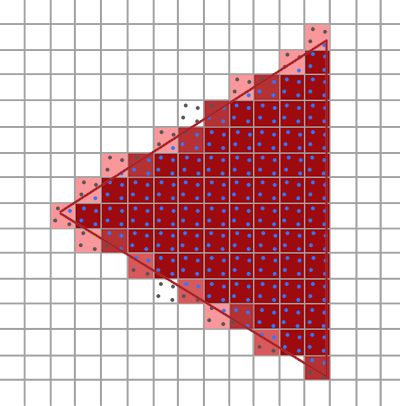
然而SSAA调用着色器的次数相当于翻了N次，这对于性能损耗是很严重的。还有一种抗锯齿技术是MSAA，它的大体思路和SSAA比较像，但是它在做子采样后，判断子采样点的覆盖信息（该采样点是否在三角形内）、遮挡信息（深度测试是否通过），将其记录下来，最后看一下有百分之多少的像素是通过覆盖、遮挡测试的，然后直接给片元着色器的计算结果乘一个百分比即可。这样，每个像素都只调用一次片元着色器，比SSAA节省了性能。当然，MSAA考虑的事情没有SSAA那么周全，所以效果是不如SSAA的。

启动SSAA：

glfwWindowHint(GLFW_SAMPLES, 4);

启动MSAA：

glfwWindowHint(GLFW_SAMPLES, 4);
glEnable(GL_MULTISAMPLE);

这样就有抗锯齿效果了：