0 引言

　　随着时代进步，越来越多的渲染技术登上历史舞台。目前最为人熟知的渲染技术是传统的管线渲染（光栅化），以及为人倾慕已久的光线追踪。两项算法技术都曾火遍一时，前者在20世纪80年代前被认为是唯一的真实感渲染算法，后者被认为是新时代最有物理依据，渲染效果最真实的算法。

　　但是事实上，两者都有难以解决的缺陷。首先是光栅化渲染，它最大的问题在于对光照的模拟尚不够真实，且难以还原透射或反射材质的外观，虽然效率十分可观，但是真实感远达不到以假乱真的水平。光线追踪虽然让画质提升了一大截，但是其计算的效率使得它只能应用于离线渲染的领域，除此之外，光追最大的问题在于它很难模拟间接光照的效果，例如Color Blending和Diffuse Reflection。为了解决上述问题，一些新的算法也随之被提出，最经典的便是辐射度算法和渲染方程。

　　本文将介绍辐射度算法基础。在介绍具体算法前，我们首先要对全局光照的辐射度有一个基本了解。

1 辐射测量

各种辐射量的定义

　　在传统的光照模拟中，我们常常使用光照的理想几何模型，即光沿直线传播、光能稳态分布、无其他场干扰。因此我们在做传统的光线追踪时，每次都从视平面发出一根光线，然后这一根光线在场景中发生多次碰撞，完成着色。但是事实上，当一根光线打在材质平面上，射出的往往不是一根光线，而是由一堆乱向的光线组成的散射。这是最传统的光线追踪没有考虑的事情，为了提高光照的真实度，我们不得不思考这种“一根光产生一片光、一片光产生一片光”的光照模型，因此辐射量的定义就诞生了。

　　辐射量就是能够描述一片光在某个区域内产生的全部影响的物理量。因为它的物理含义更加贴近真实世界，因此光照的理想几何模型就已经不够用了，我们要需要考虑更加真实的物理模型：光具有波粒二象性，即我们的工作可能会涉及到粒子模型和光照波模型。那么接下来，我们就来探究一下这些辐射量的基本定义：

0、辐射能量Q，刻画的是光源发射或光面接收到的光照能量，和热量类似，单位均为焦耳J；

1、辐射功率F或Φ，刻画的是单位时间内光源发射或受光面接受到的光照能量，单位为瓦特W，要注意的是这个量和光的传播距离、发光受光面积无关；

2、辐射能量密度E，刻画的是单位面积的辐射功率。其中入射能量密度称之为辐照度I，出射能量密度M称之为辐射度B，易得：

$$E=I=M=B=\frac{d\phi}{dA}$$

3、辐射亮度L，刻画的是单位投影面积，单位立体角内的辐射功率，换言之就是考虑光源在单位立体角内，对于单位面积的受光面投影贡献了多少功率，因此公式如下：

$$L=\frac{d^2\phi}{d\omega·dAcos\theta}$$

下图可以解释清这些符号的关系：

　　这里我们看到，右上方有一个受光面，它的面积为A；下方有一个辐射源面，它向受光面的方向上发射了光束，这个光束与光源面的法线夹角为θ；同时为了照亮受光面，光线会有一个发散角度ω。那么辐射亮度考量的就是：光源面每单位发散角度，对于受光面每单位投影面积的功率贡献值。因此L的计算方式就是：首先拿到功率总量Φ，除以发散角度ω，再除以投影后的受光面积Acosθ，那么公式就变成了：

$$L=\frac{d^2\phi}{d\omega·dAcos\theta}$$

　　以上是通过光照的波模型推出来的，从粒子角度也可以得到相似的结论。

　　我们定义光粒子的密度为p(x)，描述的是在位置x上单位体积的粒子数，因此某个区域的例子总数就是p(x)dV。考虑光子的速度为c，要穿过一个面积为dA的表面，那么在dt的时间内，通过的粒子总数为：p(x)cdtdA。

　　继续假设，若光子并非垂直于表面运动，而是拥有一个角度θ，那么通过的粒子总数便为p(x)cdtdAcosθ。继续一般化，假如光子的流动方向ω是不定的，波长λ也是不定的，那么p(x)就可以写作p(x,ω,λ)，而通过的光子总数可以用下面这个表达式来计算：

$$N=p(x,\omega,\lambda)cdtdAcos\theta d\omega d\lambda$$

　　又因为每个光子携带的能量为E=hν=hv/λ（注意前面的是ν是频率，后面的v是速度）因此接下来我们可以求出所有光量子的总能量，以及对应的功率：

$$dQ=\frac{hvp(x,\omega,\lambda)cdtdAcos\theta d\omega d\lambda}{\lambda}$$

$$d\phi=\frac{dQ}{dt}=\frac{hvp(x,\omega,\lambda)cdAcos\theta d\omega d\lambda}{\lambda}$$

　　再回到辐射亮度L，它的定义为单位体积的辐射能量，因此它的表达式为：

$$L=\int_a^b{p(x,\omega,\lambda)h\frac{c}{\lambda}d\lambda}$$

　　不难发现L和Φ的公式有重叠的部分，因此可以把辐射功率Φ和辐射亮度L联系在一起：

$$\phi=\int_A^A{\int_\omega^\omega Lcos\theta d\omega dA}$$

$$E=\int_\omega^\omega L(x←dir)cos\theta d\omega$$

$$B=\int_\omega^\omega L(x→dir)cos\theta d\omega$$

　　ps：x←dir表示来自方向dir的到达点x的辐射，x→dir表示在方向dir中留下点x的辐射。说人话就是，x←dir表示从外界dir方向射过来打到x上的光线（入），x→dir就是点x向方向dir贡献的光线（出）。

　　此外不要忘了L又与波长λ有关，因此Φ、E、B都会受波长λ影响。

辐射亮度属性

　　现在来探究一下辐射亮度的一些属性。首先我们需要做一个假设：光的传播路线上不存在任何介质（介质会吸收光能）

　　1、辐射亮度沿直线路径不变。这个属性可以通过几何推导来证明，无非就是一堆数学符号互导，就不多赘述了。这也就意味着当某一光源发射出的辐射亮度已知，那么所有点的辐射亮度分布也就确定下来了；

　　2、传感器及人眼对于辐射亮度很敏感。这就意味着传感器的响应、人眼被光照刺激的程度和辐射亮度是呈正相关的。

　　综上两条，我们可以知道物体感知颜色和亮度不随距离变化，一切都由辐射亮度来决定。因此全局光照技术一定要计算出辐射亮度，对于后续的工作有着很显著的意义。

　　（说了这么多，无非就是想和大家解释为什么这么重视辐射亮度。只要大家能了解到这个物理量的重要性就足够了）

2 光与表面的相互作用

　　接下来准备介绍图形界耳熟能详的BxDF函数了。前面我们分析了光照的各种辐射量，接下来需要考虑：当光线击中材质表面的时候，会发生什么样的行为，到底是发生折射还是反射，还是什么其他类型的透射？如果是反射，是漫反射还是镜面反射？

BRDF函数

　　事实上光线击中材质后的行为与材质属性、光线属性都息息相关，不可一概而论。针对于反射行为，我们有一种函数来描述这种行为，即双向反射分布函数BRDF（Bidirectional Reflectance Distribution Function），它描述的是出射方向上反射的相对辐射亮度与通过不同立体角入射的相对辐照度之比。这段话太长了，我们分解一下，也就是说BRDF本质上是一个比值，分子是出射方向反射的相对辐射亮度L；分母是不同立体角入射的相对辐照度E。根据前面推导的L和E的表达式，可以得到BRDF的形式为：

$$f_r(x,in→out)=\frac{dL(x→out)}{dE(x←in)}=\frac{dL(x→out)}{L(x←in)cos(N_x,in)d\omega}$$

　　上图可以辅助理解公式。换句话说，BRDF函数的输入参数分别是材质点、入射光的方向以及出射光的方向，函数返回值是该出射光亮度与入射光辐照度的比值。

　　注意：上述公式是BRDF的定义式，而非决定式。也就是说假如我们知道了入射光和出射光的物理属性，可以反推出BRDF，但是BRDF并不是由入射光和出射光来决定的，而是根据物体材质和选择的光照模型共同决定的。因此实际的逻辑应该是：根据材质和光照模型确定BRDF函数，在拿到入射光线的属性后，代入到上述定义式从而推算出来出射光线的属性。（具体如何通过材质和光照模型确定BRDF，将放在下篇文章讲述）

　　那么BxDF在实际应用中的含义是啥呢？很显然就是辅助计算光线追踪过程的光线能量，当一束带有多少能量的光击中一个表面后，它会在这个表面上发生什么，以及向不同方向反射（折射）的光线能量都是多少，这样我们就可以拿新的一批反射光线进行更深一层的tracing递归，得到更加真实、符合物理的效果。

BRDF属性

　　这个函数具有一些重要属性：

　　1、函数值域基本上可以取到任何正值，并且可以随波长变化。要注意的是BRDF描述的其实是入射辐照度E与反射相对亮度L的比值，而E和L不是一个层级的概念（一个是辐照度一个是亮度），所以不能根据“反射光一定不会强于入射光”这个常识就认为BRDF的值不能超过1。事实上函数值取多大都是可能的，if you like.

　　2、亥姆霍兹互反律，即光照的入射和反射方向互换，BRDF的函数值仍然不变。可以用以下式子表达：

$$f_r(x,in→out)=f_r(x,in←out)=f_r(x,in←→out)$$

　　3、可以推断入射与反射光线的亮度关系。前面第一条我们研究的是入射E和反射L的关系，发现关系不是很明确，因此我们进一步推导入射L和反射L的关系。这个相当简单，只需要把BRDF的式子做个移项就可以了：

$$L(x→out)=\int_\omega^\omega f_r(x,in→out)L(x←in)cos(N,in)d\omega$$

　　当然有时候我们需要考虑入射光是否真的能打到材质表面上，也就是需要引入一个取值只有0和1的可见函数V：

$$L(x→out)=\int_\omega^\omega f_r(x,in→out)L(x←in)cos(N,in)V(\omega)d\omega$$

　　这个公式概括了，如何根据入射方向、出射方向、入射亮度和材质的BRDF，来得到出射亮度。

　　4、能量守恒，这个说的就是所有方向上的反射光线总功率（能量）必须小于等于入射光线的总功率（能量）。我们知道BxDF有很多种形式，有很多种不同的理论，但是能量守恒定律是所有理论都必须遵循的一个定律。接下来我们来探究一下它的形式：

　　根据前面的推导，我们知道总入射功率E的表达式为：

$$E=\int_\omega^\omega L(x←in)cos\theta d\omega$$

　　出射功率B的表达式为：

$$B=\int_\omega^\omega L(x→dir)cos\theta d\omega$$

　　将未知量L(x→out)用第三条的式子替代，就变成了：

$$B=\int_\omega^\omega \int_\omega^\omega f_r(x,in→out)L(x←in)cos(N_x,out)cos(N_x,in)d\omega_{in} d\omega_{out}$$

　　根据能量守恒定律，出射幅度与入射幅度的比值不能超过1，因此公式可以写作：

$$\frac{\int_\omega^\omega \int_\omega^\omega f_r(x,in→out)L(x←in)cos(N_x,out)cos(N_x,in)d\omega_{in} d\omega_{out}}{\int_\omega^\omega L(x←in)cos\theta d\omega}\le1$$

　　这个定律外加上亥姆霍兹互反律，都是用来检测开发人员定义的BRDF模型是否符合基本物理原理的公式，是特别重要的约束条件。由此我们理解了BRDF分布函数的实质和特性，接下来我们来看一些BRDF的典型例子。

BRDF实例

　　常见的3类反射表面包括纯粹漫反射表面、纯粹镜面和光泽表面，前两个可以通过公式来精确求解，后者属于前两者的一个混合，随机性较强，就不详细介绍了。

　　1、纯粹漫反射表面

　　纯粹漫反射，意味着这种材质不管接收到什么方向来的光线，都会均匀地向各个方向反射，那么它的BRDF也就是个定值：

$$f_r(x)=\frac{\rho_d}{\pi}$$

　　ρ指的其实是反射率，是基于物理的渲染（pbr）模型中常见的可调参数。那么这个BRDF的值说明了在纯粹漫反射表面上，出射亮度与入射辐射度的比值是个定值，且具体出射亮度的大小将由反射率决定。

　　这里大家思考一下，传统的光线追踪是怎么模拟这个模型的？是一根光线击中平面后，选择一个随机的方向进行反射。虽然看起来也是“均匀漫反射”，但是本质上还是一根光线入一根光线出，而BRDF的均匀漫反射就做到了将一根光线产生的全部影响全部描述到位，这就突出了辐射量算法的“全局性”。

　　2、纯粹镜面（反射）

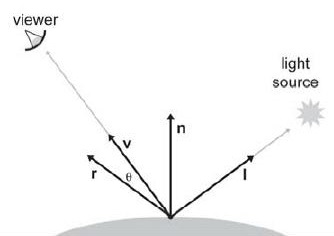
　　镜面反射也是一个比较基础的反射模型了，纯粹镜面就是只能在一个特定的方向上反射光线。假设入射向量为I，法线为N，反射向量为R，很容易得到：

$$\frac{\pmb I+\pmb R}{2}=(\pmb N · \pmb I)\pmb N$$

$$\pmb R=2(\pmb N · \pmb I)\pmb N -\pmb I$$

　　根据上述式子，我们可以确定反射方向。这意味着：如果纯粹镜面收到一个方向向量为I的光线，那么只有方向向量为R的那个out方向才有亮度输出，即：

$$f_r(x,in→out)>0，当in和out满足上述R与I的关系式$$

$$f_r(x,in→out)=0，当in和out不满足上述R与I的关系式$$

　　在图形界很少使用上述分类讨论的形式，而是使用狄拉克δ函数来代替（只有自变量为0时，因变量才不为0；自变量非0时因变量均为0）。当然这种情况其实就和传统的光线追踪一样，入射光线是一根，对应的出射光线也是一根。

BTDF函数

　　前面的BRDF函数只能描述反射，然而光照是包括透射的，因此我们也有相应的BTDF函数（Bidirectional Transmission Distribution Function）。透射其实也有很多情况但这里只介绍一个折射。折射其实是初中物理的知识了，我们直接套用斯涅尔定律：当入射材质的折射率为η1，折射材质的折射率为η2时，满足：

$$\eta_1sin\theta_1=\eta_2sin\theta_2$$

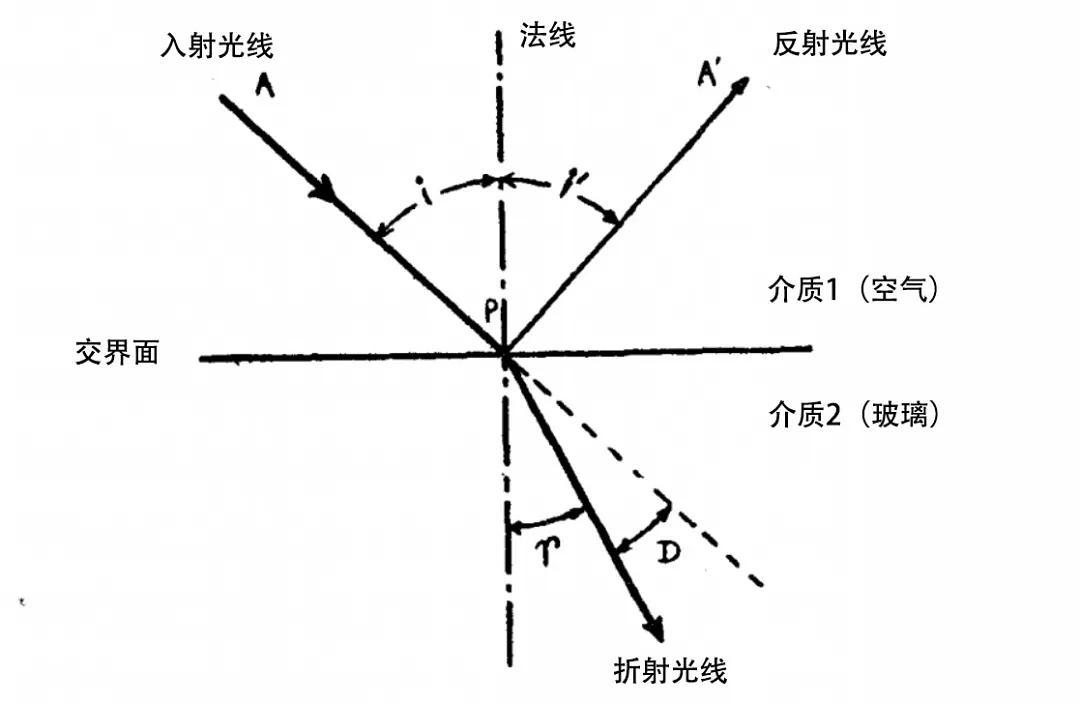
　　当我们获取到两个材质的折射率、夹角、法线以及入射光线时，透射光线的表达式如下：

$$T=-\frac{\eta_1}{\eta_2}\pmb I+N(\frac{\eta_1}{\eta_2}cos\theta_1-\sqrt{1-(\frac{\eta_1}{\eta_2}^2(1-cos\theta_1^2)})$$

$$cos\theta_1=\pmb N·\pmb I$$

$$T=-\frac{\eta_1}{\eta_2}\pmb I+N(\frac{\eta_1}{\eta_2}cos\theta_1-\sqrt{1-(\frac{\eta_1}{\eta_2}^2(1-(\pmb N·\pmb I)^2)})$$

　　公式看起来挺复杂的，但对于这种没涉及积分的式子，计算机的处理能力还是非常强的。接下来我们回忆一下初中物理：当光从稠密介质传输到稀疏介质时，其折射后与法线的夹角将会变大，那么假如其与法线间的夹角大到了90°，就会出现全内反射，即不再出现折射光线，而是全部都进行反射，很显然全内反射的临界角的正弦值等于介质折射率之比（可以从斯内尔定律推，也可以从上述折射光线T的表达式推，很简单所以不多赘述了）

BSDF函数

　　反射是reflection，对应的函数是BRDF；透射是transmission，对应的函数是BTDF；把反射和透射混在一起讨论，就形成了散射（scattering），对应的函数是BSDF（Bidirectional scattering distribution function）。BSDF失去了一条BRDF的属性，那就是互反律。这是因为一旦讨论到透射，那就涉及各种介质，而不同的介质会不同程度地消耗光线能量，因此亥姆霍兹互反律在BSDF函数中就不适用了。

　　既然BSDF既包括折射又包括反射，那怎么确定有多少能量是折射，有多少能量是反射呢？这里就要用到菲涅尔方程了。它描述的就是当光线照射在完美光滑的平面上时，反射占比R（透射占比就是1-R）是多少。当然菲涅尔方程严谨在：考虑了偏振光不同偏振方向的反射比率。即当一束光是偏振光时：

$$R_p=\frac{\eta_2cos\theta_1-\eta_1cos\theta_2}{\eta_2cos\theta_1+\eta_1cos\theta_2}$$

$$R_s=\frac{\eta_1cos\theta_1-\eta_2cos\theta_2}{\eta_1cos\theta_1+\eta_2cos\theta_2}$$

　　当光束不是偏振光时：

$$R=\frac{|r_p|^2+|r_s|^2}{2}$$

$$T=1-R$$

　　举一个例子，下图展示了光线从空气射向不同材质时的菲涅耳反射比，可以看到金属比电解质更容易产生反射（常识）；对于同一种材质，随着入射角增大，反射率也在逐渐增大。

　　那么三类BxDF就介绍完毕了。接下来我在blender中做了一个马灯模型，然后对其中的灯罩部分分别上了BTDF、BRDF、BSDF的材质，结果如下：

　　本文重点介绍了辐射度算法和BxDF的基本原理，接下来将探究BxDF的光照模型或其它经验模型。