BRDF光照模型与渲染方程
- 23 5 月, 2021
- by
- pladmin
0 引言
上一篇文章讲述了BRDF、BTDF、BSDF的基本原理,也介绍了BxDF的定义式。但上一篇文章也提到了,真正决定BxDF函数值的不是入射光和出射光,而是材质和光照模型。光照模型决定了BRDF的计算公式,而材质决定了计算公式的输入参数。
本文的目的就是介绍几种极其经典的光照模型,体验它们计算双向分布函数的方法。(注:原书错把光照模型译作着色模型,事实上这里我们讨论的是光照模型,即如何定义光照相关的公式;而着色模型说的是计算频率与片元插值相关的事,切勿混淆)
1 光照模型
反射的光照模型有许多种,但大部分BRDF函数都由两部分组成,一个是漫反射项(diffuse reflection),另一个是镜面/高光反射项(specular reflection),分别用d和s来表示。对于漫反射项,其对应的BRDF值是一个定值,与入射光、出射光的方向无关,因此无论反射光照指向哪个方向,其强度都是相同的;而对于镜面反射项,其BRDF值的计算方式就各不相同了,一般可以写作g()·ks(其中g()要与入射光、出射光的方向有关)即镜面反射系数乘上一个光照模型计算出来的函数值。一般光照模型都是由上述漫反射项和镜面反射项共同构成,因此通用的BRDF公式大体可以写作如下形式:
$$f_r=g()k_s+k_d$$
那么接下来我们就来看几个经典的BRDF光照模型,每个模型都拥有一个不同的g(),即拥有一个不同的BRDF计算模型。在分析完公式以后,我将尝试在unity中编写对应shader,来模拟、观察当前光照模型的BRDF结果。
(这里可能有同学会感到疑惑,BRDF的目的是计算出射光线的属性,然而unity中用的是管线渲染而不是光线追踪,计算出射光线有什么意义呢?事实上大部分出射光线确实是没意义的,但有一根出射光线至关重要:那就是从材质表面反射到相机中的光线,这个光线所携带的颜色和强度决定了你眼中的画面。因此在unity这种管线渲染中,入射光线就是光源到材质表面的向量,而出射光线我们只计算从材质表面到相机的这根向量,方法依然是套用BRDF的定义式。这就是BRDF在非光追的管线渲染技术中的用处。)
Lambert模型
兰伯特反射模型可以说是BRDF光照模型的Hello World,它是一个专门针对理想化漫反射材质而设计的模型,即只存在漫反射,不存在镜面反射(即g()=0),因此其BRDF相当简单:
$$f_r=k_d=\frac{\rho_d}{\pi}$$
这个BRDF值说明了,反射光线强度与入射光线强度成正比,与反射角度无关。因此无论从什么角度去看材质,最后反射到相机里的光强都是一样的。
设入射光线向量为in,从材质射入相机的向量为out,击中点的法线为N,光线强度系数为s,那么在渲染器中入射光线的强度可以用下列算式表示:
$$L(in)=\pmb{in}·\pmb N·s$$
那么反射光线的强度就是:
$$L(out)=L(in)·f_r=\pmb{in}·\pmb N·s·k_d$$
接下来可以编写shader了。思路无非就是三步:转法线、算反射、顶点空间变换:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 | Shader "Puluo/Lambert" { Properties { _Color("Color", color) = (1.0,1.0,1.0,1.0) _Lightness("Lightness",float)=1.0 } SubShader{ Pass{ Tags { "LightMode" = "ForwardBase"} CGPROGRAM #pragma vertex vert #pragma fragment frag uniform float4 _Color; uniform float _Lightness; uniform float4 _LightColor0; struct vertexInput { float4 vertex:POSITION; float3 normal:NORMAL; }; struct vertexOutput { float4 pos:SV_POSITION; float4 col:COLOR; }; vertexOutput vert(vertexInput v) { vertexOutput o; float3 normalDirection = normalize(mul(float4(v.normal,0.0),unity_WorldToObject).xyz);//将模型空间的法线转到世界空间 float3 lightDirection; lightDirection = normalize(_WorldSpaceLightPos0.xyz);//灯光方向 float3 diffuseReflection = _Lightness * _LightColor0.xyz * max(0.0, dot(normalDirection,lightDirection));//计算兰伯特漫反射 float3 lightFinal = diffuseReflection + UNITY_LIGHTMODEL_AMBIENT.xyz;//与环境光结合 o.col = float4(lightFinal * _Color.rgb,1.0); o.pos = UnityObjectToClipPos(v.vertex); return o; } float4 frag(vertexOutput i) :COLOR { return i.col; } ENDCG } } } |
Lightness就是上述公式中涉及到的s*k_d,这里作为可调参数;在顶点着色器中,首先将模型空间的法线变换到世界空间,然后拿到灯光方向,便可套用上述L(out)的表达式计算出漫反射项强度了。接下来加一个环境光填补,然后和漫反射颜色Color进行一个混合,便得到了最简单的兰伯特光照模型:(是动图,只不过帧率有点低)

无论从什么视角去看,它的材质表面颜色都是不变的。这就是兰伯特模型(即纯漫反射)的效果:对于所有出射光,其能量都是相同的,都是入射光的kd倍。
Phong模型
从Phong模型开始,漫反射项和镜面反射项就同时存在了。其BRDF公式多了一个变量R,记录的是入射光线在材质上的镜面反射向量(不要和out混淆,out指的是从材质片元到相机的向量)。该模型的各个公式如下:
$$\pmb R=2(\pmb N · \pmb I)\pmb N -\pmb I$$
$$f_r=k_s\frac{(\pmb R·\pmb {out})^n}{\pmb N·\pmb {in}}+k_d$$
$$L(in)=\pmb{in}·\pmb N·s$$
$$L(out)=L(in)·f_r=\pmb{in}·\pmb N·s·(k_s\frac{(\pmb R·\pmb {out})^n}{\pmb N·\pmb {in}}+k_d)$$
镜面反射部分告诉我们,不同方向的反射光线强度一定是有区别的(不然就成均匀漫反射了),反射到相机的向量越靠近镜面反射,则显示出来的光强度越强。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 | Shader "Puluo/Phong" { Properties { _Color("Color", color) = (1.0,1.0,1.0,1.0) _Specular("nspecular",float) = 0 _ks("kspecular",float) = 0 _kd("kdiffuse",float) = 1 _s("s",float) = 1 } SubShader { Tags { "RenderType" = "Opaque" } LOD 100 Pass { CGPROGRAM #pragma vertex vert #pragma fragment frag #include "UnityCG.cginc" struct v2f { float2 uv : TEXCOORD0; float4 vertex : SV_POSITION; float3 normal : TEXCOORD1; float3 lightDir : TEXCOORD2; float4 objPos : TEXCOORD3; }; float4 _LightColor0; float _Specular; float _ks; float _kd; float _s; float4 _Color; v2f vert(appdata_full v) { v2f o; o.objPos = v.vertex; o.vertex = UnityObjectToClipPos(v.vertex); o.normal = v.normal; return o; } fixed3 frag(v2f i) : SV_Target { float3 L = normalize(_WorldSpaceLightPos0.xyz); float3 N = normalize(mul(float4(i.normal, 0.0), unity_WorldToObject).xyz); float3 viewDir = normalize(ObjSpaceViewDir(i.objPos));//计算出视线 float lightness = saturate(dot(L, N)); float3 reflection = normalize(2*dot(N,L)*N-L); float spec = pow(max(0, dot(reflection, viewDir)), _Specular); spec /= lightness; float f = spec * _ks + _kd; float3 col = f * lightness * _s * _LightColor0.xyz + UNITY_LIGHTMODEL_AMBIENT.xyz; col = col * _Color; return col; } ENDCG } } } |
这里公开了5个变量,Color就是默认的材质颜色,Specular对应了公式的n,ks对应ks,kd对应kd,s对应s,效果如下:

通过gif能清晰地看到,改变n则改变了高光区域的大小及柔和程度,改变ks则改变了高光的整体亮度,改变kd则改变了非高光区域的亮度,s控制了整体光的亮度。
Blinn-Phong模型
Blinn-Phong模型的特点在于,去掉了镜面反射向量R,引入了一个半程向量H,即in和out的中间向量。BRDF的公式和Phong模型很像,只是把分子中的R·out改成了N·H,即:
$$f_r=k_s\frac{(\pmb N·\pmb H)^n}{\pmb N·\pmb {in}}+k_d$$
思路和Phong模型没什么区别,就改动了一小部分高光项。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 | Shader "Puluo/BlinnPhong" { Properties { _Color("Color", color) = (1.0,1.0,1.0,1.0) _Specular("nspecular",float) = 0 _ks("kspecular",float) = 0 _kd("kdiffuse",float) = 1 _s("s",float) = 1 } SubShader { Tags { "RenderType" = "Opaque" } LOD 100 Pass { CGPROGRAM #pragma vertex vert #pragma fragment frag #include "UnityCG.cginc" struct v2f { float2 uv : TEXCOORD0; float4 vertex : SV_POSITION; float3 normal : TEXCOORD1; float3 lightDir : TEXCOORD2; float4 objPos : TEXCOORD3; }; float4 _LightColor0; float _Specular; float _ks; float _kd; float _s; float4 _Color; v2f vert(appdata_full v) { v2f o; o.objPos = v.vertex; o.vertex = UnityObjectToClipPos(v.vertex); o.normal = v.normal; return o; } fixed3 frag(v2f i) : SV_Target { float3 L = normalize(_WorldSpaceLightPos0.xyz); float3 N = normalize(mul(float4(i.normal, 0.0), unity_WorldToObject).xyz); float3 viewDir = normalize(ObjSpaceViewDir(i.objPos)); float3 H = normalize(L+viewDir); float lightness = saturate(dot(L, N)); float3 reflection = normalize(2*dot(N,L)*N-L); float spec = pow(max(0, dot(N, H)), _Specular); spec /= lightness; float f = spec * _ks + _kd; float3 col = f * lightness * _s * _LightColor0.xyz + UNITY_LIGHTMODEL_AMBIENT.xyz; col = col * _Color; return col; } ENDCG } } } |
最终效果和Phong模型较为相似,所以就不单上gif了,唯一的区别就是高光部分会更加自然。
但是上述式子有一个很严重的问题,就是不满足亥姆霍兹互反律。虽然Blinn-Phong在管线渲染中使用颇为广泛,但是上篇文章讲到了亥姆霍兹互反律是检验BRDF模型是否符合物理学的依据之一,因此这个模型是不能称作合格的BRDF模型的。后来有人对模型进行了改进,例如去掉分母的N·in,但也不能完全解决问题。
Cook-Torrance模型
Cook-Torrance模型其实有点超纲了,是属于基于物理的渲染(Physically Based Rendering)那个专区的内容,因此在这里就不详细解释,直接列公式、莽shader了。它最大的特点在于使用了一种微平面模型,即假设表面由随机的小平滑平面集合组成:
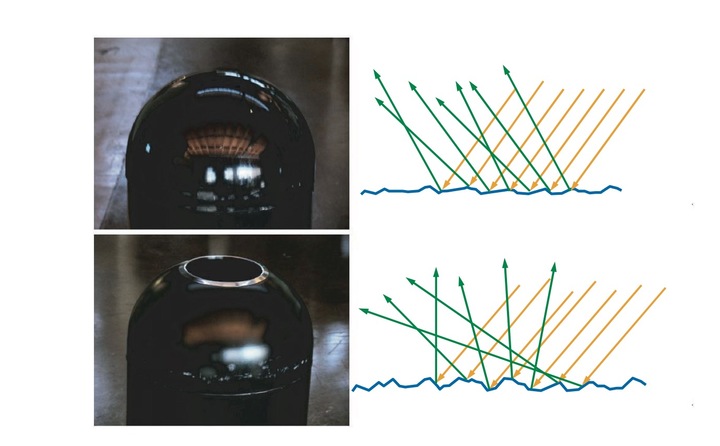
既然有了微表面的概念,那微表面一定会引起一些遮挡现象,因此公式中需要引入几何阴影项;同时模型也考虑了上一篇文章提到的菲涅尔方程,其BRDF公式如下:
$$f_r=\frac{F(\beta)D(\theta_h)G}{\pi(\pmb N·\pmb {in})(\pmb N·\pmb {out})}+k_d$$
这里面F指的是菲涅尔方程,D指的是为平面分布函数,G指的是几何阴影项。接下来列出它们的式子,具体来源和推导会在pbr专区讲解:
$$F_p=\frac{\eta_2cos\theta_1-\eta_1cos\theta_2}{\eta_2cos\theta_1+\eta_1cos\theta_2}(偏振光p方向)$$
$$F_s=\frac{\eta_1cos\theta_1-\eta_2cos\theta_2}{\eta_1cos\theta_1+\eta_2cos\theta_2}(偏振光s方向)$$
$$F=\frac{|F_p|^2+|F_s|^2}{2}(非偏振光)$$
$$D(\theta_h)=\frac{1}{m^2cos^4\theta_h}e^{-(\frac{tan\theta_h}{m})^2}$$
$$G=min[1,\frac{2(\pmb N·\pmb H)(\pmb N·\pmb {out})}{\pmb{out}·\pmb H},\frac{2(\pmb N·\pmb H)(\pmb N·\pmb {in})}{\pmb{out}·\pmb H}]$$
在这里皮一下,把Cook-Torrance模型的BRDF函数完全展开:
$$f_r=\frac{(\frac{|\frac{\eta_2cos\theta_1-\eta_1cos\theta_2}{\eta_2cos\theta_1+\eta_1cos\theta_2}|^2+|\frac{\eta_1cos\theta_1-\eta_2cos\theta_2}{\eta_1cos\theta_1+\eta_2cos\theta_2}|^2}{2})(\frac{1}{m^2cos^4\theta_h}e^{-(\frac{tan\theta_h}{m})^2})(min[1,\frac{2(\pmb N·\pmb H)(\pmb N·\pmb {out})}{\pmb{out}·\pmb H},\frac{2(\pmb N·\pmb H)(\pmb N·\pmb {in})}{\pmb{out}·\pmb H}])}{\pi(\pmb N·\pmb {in})(\pmb N·\pmb {out})}+k_d$$
事实上这一坨式子很难编程,例如菲涅尔公式中的偏振状况和折射率求解都不是很方便,因此我们可以对公式进行一点小的简化:
$$F=F_0+(1-F_0)(1-(\pmb out·\pmb H))^5$$
为了便于编程,继续把D中的三角函数换成向量表达的形式:
$$D=\frac{1}{4m^2(\pmb N·\pmb H)}e^{\frac{(\pmb N·\pmb H)^2-1}{m^2(\pmb N·\pmb H)^2}}$$
接下来可以编程了。但是事实上它的效果和pbr的相似度比较高,大家可以直接观察unity默认的standard材质效果即可,所以也就不放代码和效果图了、
2、渲染方程
回到之前的问题,为什么我们没有满足于简单光照几何模型,而深入到真实物理层面去分析光线属性呢?这是因为我们要对整个光照环境做一个完整、准确的度量。只有光照环境处处符合物理学,才能完成最真实的渲染效果,这就是我们研究全局光照的目的。而渲染方程,本质上就是光照学中的能量守恒定律,只要根据渲染方程来计算光线的性质,一定能得到最符合真实世界的环境渲染。
前面我们介绍了一些基础的辐射学公式,以及新引入了BxDF的概念,有了这些基础,我们便可以快速推出强大的渲染方程了。事实上,渲染方程也有不同的形式,主要取决于如何定义入射光的来源。下面将介绍几种经典的渲染方程。
半球形公式
半球形公式考虑的是:对于点x,入射光来源于以该点为球心的上半球。我们知道从x点发出的光线可以包括两部分内容:一部分是自发光发出来的,另一部分就是入射光的反射。因此我们的出射亮度可以写作这个形式:
$$L(x→out)=L_e(x→out)+L_r(x→out)$$
根据BRDF的定义,可以得到:
$$f_r(x,in→out)=\frac{dL_r(x→out)}{dE(x←in)}$$
$$L_r(x→out)=\int_\omega^\omega f_r(x,in→out)L(x←in)cos(N,in)d\omega$$
两个式子合在一起,就成为了最终的渲染方程:
$$L(x→out)=L_e(x→out)+\int_\omega^\omega f_r(x,in→out)L(x←in)cos(\pmb N,\pmb {in})d\omega$$
区域公式
区域公式换了一个思路:对于点x,其入射光的来源是场景中所有可见的物体表面。因此该公式本质上是对该点可见的所有表面上出射光的积分,用它来直接替代球面积分。
根据区域公式的定义,对于被照射点x与任意表面上的任意点y,首先要计算它们之间的“可见性”。如果可见,那么积分就需要包括y点,否则就不包括。我们可以用一个布尔类型的函数V(x,y)来表示可见性,若可见则V(x,y)=1,若不可见则V(x,y)=0。
此外,我们知道x点的入射光就是y点的出射光,因此:
$$L(x←in)=L(y→-in)$$
既然现在不是半球形公式了,那么原本立体角的含义也有所改变:
$$d\omega=d\omega_{x←dA_y}=cos(\pmb {N_y},-\pmb {in})\frac{d\pmb{A_y}}{r_{xy}^2}$$
把上述式子代入到原先的半球形公式中,新的渲染方程即为:
$$L(x→out)=L_e(x→out)+\int_A^A f_r(x,in→out)L(y→-in)V(x,y)cos(\pmb N,\pmb {in})cos(\pmb {N_y},-\pmb {in})\frac{dA_y}{r_{xy}^2}$$
直接照明与间接照明
直接照明指的是光从光源直接照到材质表面,间接照明指的是光在场景中经过反射若干次后照到材质表面。经验表明,当考虑直接光的时候,区域公式更有效;考虑间接光的时候,半球形公式更有效。可以这样去想这件事:直接光一定是从光源发出来的、没有经过反射的,因此其来源一定是光源,我们可以很轻松找到光源并在其表面区域上进行积分;而对于间接光,由于其光线经过反射,因此很难找到其来源,所以只能使用半球形公式。于是我们可以把渲染方程进行分解:
$$L(x→out)=L_e(x→out)+L_r(x→out)$$
$$L(x→out)=L_e(x→out)+L_{direct}+L_{indirect}$$
将两者的渲染方程直接代入:(因为公式太长所以分行写了)
$$L(x→out)=L_e(x→out)+$$
$$\int_A^A f_r(x,in→out)L(y→-in)V(x,y)cos(\pmb N,\pmb {in})cos(\pmb {N_y},-\pmb {in})\frac{dA_y}{r_{xy}^2}+$$
$$\int_\omega^\omega f_r(x,in→out)L(x←in)cos(\pmb N,\pmb {in})d\omega$$
如此便得到了一个考虑情况更加周全、更加好用的渲染方程。