Opengl实时渲染器(四)高级光照与阴影的着色
- 10 4 月, 2023
- by
- pladmin
引言
本篇我们来复现一下opengl的blinn-phong模型、shadow map技术、法线贴图、HDR等内容。这篇的难度略大,有许多复杂的公式和晦涩的算法要钻研。
Part1. Blinn-Phong光照模型
Phong模型是个很高效的光照模型,但是存在一个比较明显的问题,那就是当物体反光度很低时,会导致大片(粗糙的)高光区域,所以后来就又引申出来一个新的光照模型——Blinn-Phong模型来解决这个问题,直接上公式:
$$L_{out} = L_{light} * (\rho_d * dot(n,l) + \rho_s*dot(N,H)^n)$$
$$H = \frac{l + v}{|| l + v ||}$$
所以代码只需简单修改:
for(int i = 0; i < 6; i++){
if(dl[i].color == vec3(0,0,0)) continue;
vec3 lightDir = normalize(-dl[i].dir);
vec3 h = (lightDir + viewDir) / length(lightDir + viewDir);
float cosine = max(dot(norm, lightDir), 0.0);
vec3 reflectDir = reflect(-lightDir, norm);
float cosine2 = pow(max(dot(norm, h), 0.0), material.shininess_n);
FragColor += vec4(dl[i].color * (vec3(rho_d) * cosine + rho_s * cosine2), 0.0);
}
for(int i = 0; i < 6; i++){
if(pl[i].color == vec3(0,0,0)) continue;
vec3 lightDir = normalize(pl[i].pos - f_FragPos);
vec3 h = (lightDir + viewDir) / length(lightDir + viewDir);
float distance = length(pl[i].pos - f_FragPos);
float cosine = max(dot(norm, lightDir), 0.0);
vec3 reflectDir = reflect(-lightDir, norm);
float cosine2 = pow(max(dot(norm, h), 0.0), material.shininess_n);
vec3 pl_color = pl[i].color / (pl[i].constant + pl[i].linear * distance + pl[i].quadratic * distance * distance);
FragColor += vec4(pl_color * (vec3(rho_d) * cosine + rho_s * cosine2), 0.0);
}
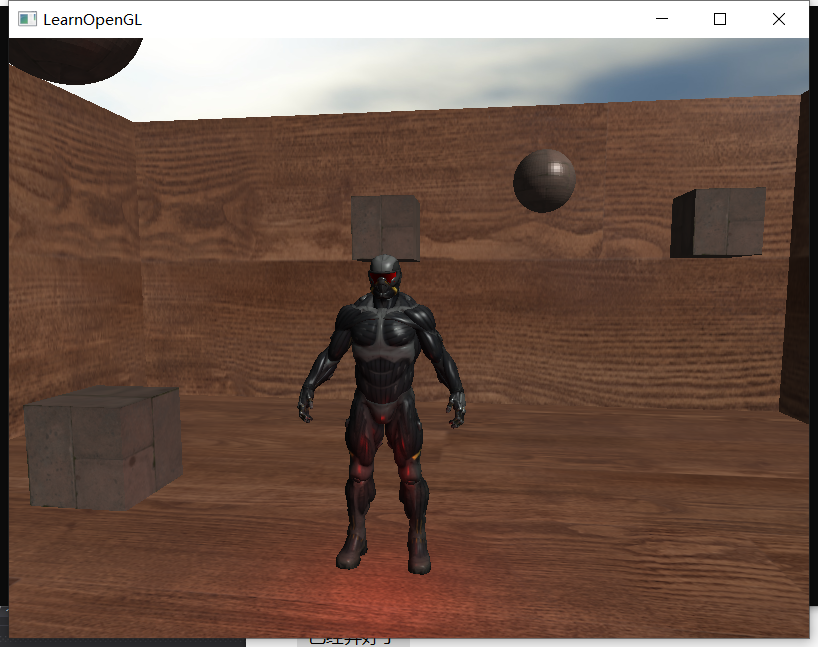
现在看效果发现挺不明显的,可能因为缺少墙体、地板,所以光线整体效果体现不出来。所以我重新做了一份场景来演示blinn-phong的效果:
Part2. Gamma矫正
直接套用公式:
$$rgb_{gamma} = {rgb_{linear}} ^ {\frac{1}{2.2}}$$
Gamma矫正应该属于后处理阶段,因此我们将矫正行为放在PostProcessShader中进行:
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
uniform sampler2D screenTexture;
void main()
{
vec3 colors = vec3(texture(screenTexture, TexCoords));
//这里对colors进行后处理
FragColor.rgb = pow(colors,vec3(1/2.2));
FragColor.a = 1.0;
}
得到效果:
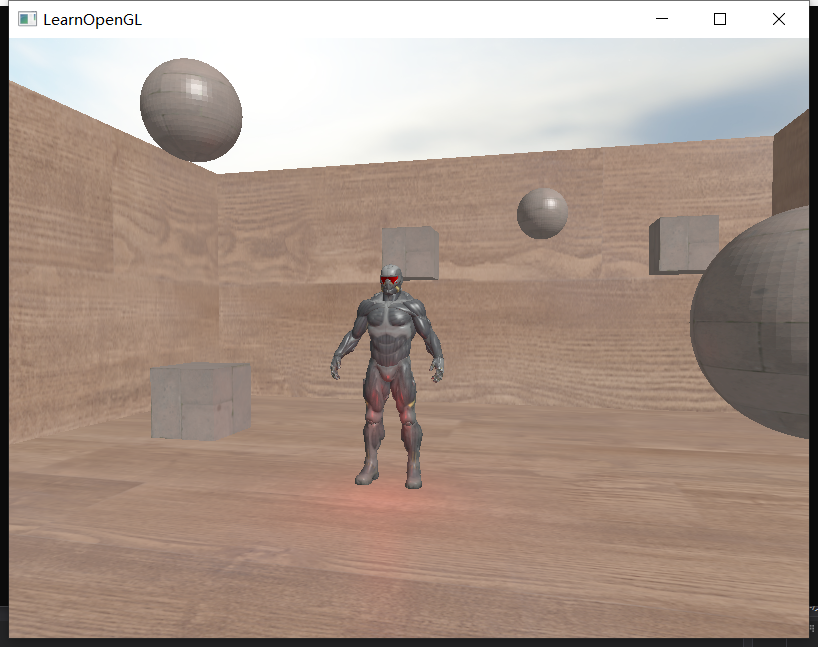
矫正后场景就更亮一些了。这里也埋了一个小坑:我们使用的纹理其实大部分在制作时就被gamma矫正过了,而此时我们再使用一次gamma矫正,纹理部分相当于被矫正了两次,所以会整体发白。所以我们采样diffuse纹理的时候可以先对其做一次逆gamma矫正:
vec4 rho_d;
if(material.diffuse_texture_use == true) {
rho_d = texture(material.diffuse_texture, f_texcoord);
rho_d.rgb = pow(rho_d.rgb,vec3(2.2));
}
这样纹理就不会发白了:
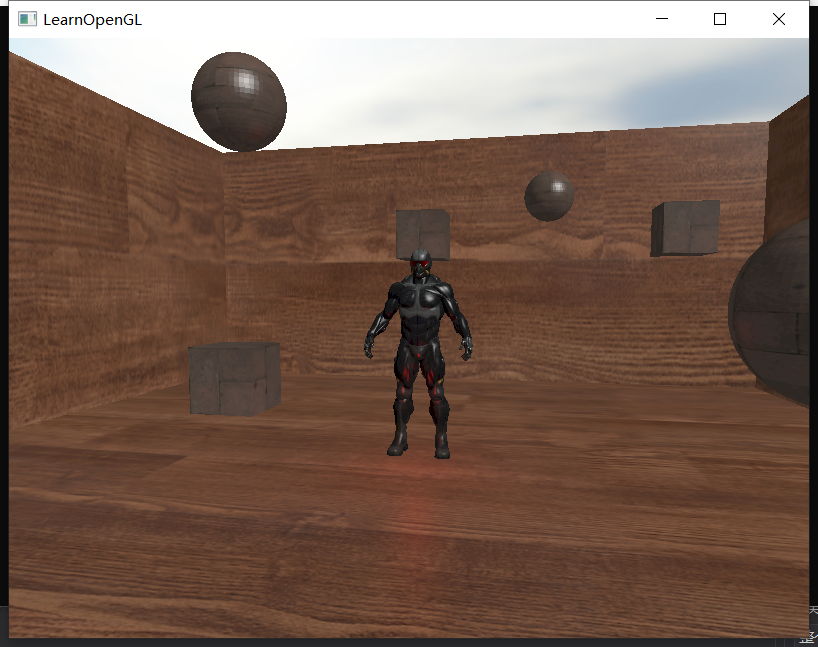
Part3. 直接光阴影
现在迎来本篇的第一个难题,就是实时阴影。其实早在2年前我就写过一篇过于实时阴影技术的blog:ShadowMap及PCF阴影技术 – PULUO,但是我回顾了一下这些2年前写的文章,大部分都是不求甚解、知识不成体系,换句话说我当时可能压根就没学明白,以至于我现在都想给这几篇blog定义为垃圾blog(2年前的我:你再骂)
现在我们来重新捋一下直接光的shadowmap技术流程。首先我们将相机代换到光源位置,相机方向就沿着直接光照的方向,按照管线流程跑一遍渲染,此时拿到每一个像素的深度数据,存入一张深度纹理中;然后我们将相机还原到真正的场景位置中跑渲染,对于每一个枚举到的片元,对比一下“其与直接光源的距离”和“该片元在深度纹理中对应像素的深度值”哪个更大。如果前者明显比后者大,说明这个片元被其他物体挡住了;如果前者和后者几乎相等,说明这个片元可以直接被光给照射到。
所以流程就是:①跑一遍光源视角的渲染,保存深度纹理(这个深度纹理是光源透视空间下的纹理);②在相机视角渲染的时候,将每个片元变换到光源透视空间下,求其坐标,根据这个坐标采样出深度纹理中的深度值;③对比光源距离和采样得到的深度值,相等则进行光源着色,后者明显小就留阴影。
简单起见,我们先考虑只有一盏直接光的情况。
1、深度缓冲与贴图绑定
因为我们一开始要从光源视角做渲染,然后把其中的深度值单独拿出来存入纹理,所以我们需要自定义一张深度缓冲区和存深度值的纹理:
/*阴影缓冲设置*/
GLuint depthMapFBO;
glGenFramebuffers(1, &depthMapFBO);
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
/*阴影纹理设置*/
const GLuint SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024;
GLuint depthMap;
glGenTextures(1, &depthMap);
glBindTexture(GL_TEXTURE_2D, depthMap);
glTexImage2D(GL_TEXTURE_2D, 0, GL_DEPTH_COMPONENT, SHADOW_WIDTH, SHADOW_HEIGHT, 0, GL_DEPTH_COMPONENT, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_TEXTURE_2D, depthMap, 0);
glDrawBuffer(GL_NONE);
glReadBuffer(GL_NONE);
glBindFramebuffer(GL_FRAMEBUFFER, 0);
自定义的缓冲区用来接收渲染结果,然后自动地将其中的深度数据写入我们绑定的纹理中。接下来我们开始设置渲染,首先我们要给予shader一个空间变换的矩阵,这个描述了灯视角的变换:
/////////////////////////这里开始光源视角渲染
glEnable(GL_DEPTH_TEST);
shader_dir_light.use();
glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glClear(GL_DEPTH_BUFFER_BIT);
GLfloat near_plane = 1.0f, far_plane = 500.0f;
glm::mat4 lightProjection = glm::ortho(-40.0f, 40.0f, -40.0f, 40.0f, near_plane, far_plane);
glm::mat4 lightView = glm::lookAt(glm::vec3(40.0f, 40.0f, 40.0f), glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, 1.0f, 0.0f));
glm::mat4 lightSpaceMatrix = lightProjection * lightView;
glm::mat4 model = glm::identity<glm::mat4>();
shader_dir_light.setMatrix("lightSpaceMatrix", lightSpaceMatrix);
shader_dir_light.setMatrix("model", model);
models->Draw(shader_dir_light);
glBindFramebuffer(GL_FRAMEBUFFER, 0);
首先灯源视角的视口大小不再是窗口大小了,而是设定的深度纹理的尺寸;然后我们计算一下所有物体的模型-世界矩阵、世界-视角矩阵、透视(正交)矩阵即可。
光源视角的shader比较简单:
///////////////////////Vertex Shader///////////////////////
#version 330 core
layout (location = 0) in vec3 position;
uniform mat4 lightSpaceMatrix;
uniform mat4 model;
void main()
{
gl_Position = lightSpaceMatrix * model * vec4(position, 1.0f);
}
///////////////////////fragment Shader///////////////////////
#version 330 core
void main()
{
}
只需要将世界中所有物体顶点变换到视角中对应位置即可,片元着色器甚至可以留空,因为最后我们只需要一个深度值。最后可以得到这样的效果:
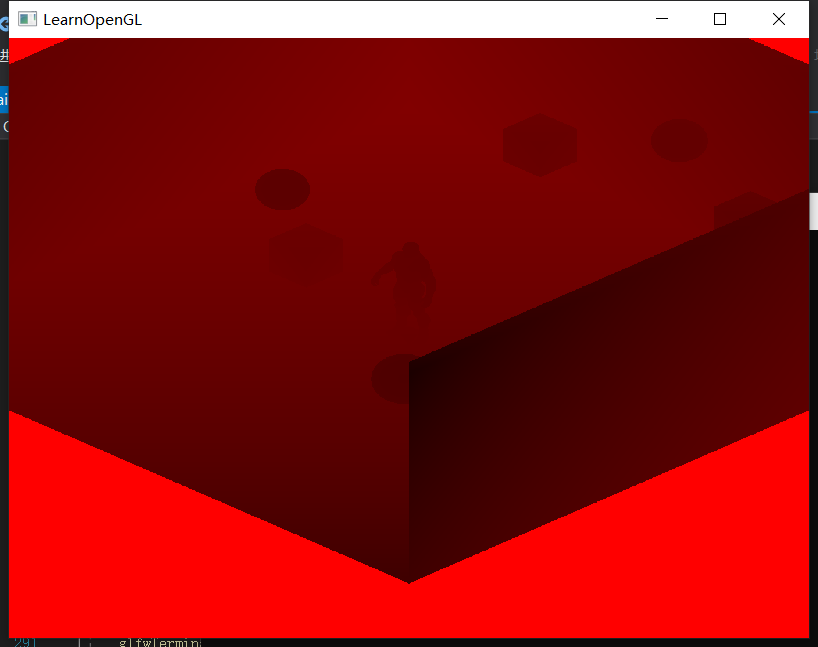
要根据场景的实际尺寸来调整正交矩阵的尺寸、远裁剪平面的距离。
2、正经渲染时采样深度纹理
现在我们得到了一张深度纹理,这张纹理送入到我们的普通shader中去做采样。普通shader的片元着色器作如下修改:
...
uniform mat4 lightSpaceMatrix;
uniform sampler2D shadowMap;
...
float cal_dir_shadow()
{
vec4 fragPosLightSpace = lightSpaceMatrix * f_FragPos;
// 执行透视除法
vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w;
// 变换到[0,1]的范围
projCoords = projCoords * 0.5 + 0.5;
// 取得最近点的深度(使用[0,1]范围下的fragPosLight当坐标)
float closestDepth = texture(shadowMap, projCoords.xy).r;
// 取得当前片段在光源视角下的深度
float currentDepth = projCoords.z;
// 检查当前片段是否在阴影中
float shadow = currentDepth > closestDepth ? 1.0 : 0.0;
return shadow;
}...
void main()
{
vec3 norm = normalize(f_normal);
...
for(int i = 0; i < 6; i++){
if(dl[i].color == vec3(0,0,0)) continue;
vec3 lightDir = normalize(-dl[i].dir);
vec3 h = (lightDir + viewDir) / length(lightDir + viewDir);
float cosine = max(dot(norm, lightDir), 0.0);
vec3 reflectDir = reflect(-lightDir, norm);
float cosine2 = pow(max(dot(norm, h), 0.0), material.shininess_n);
float shadow = cal_dir_shadow();
FragColor += vec4(dl[i].color * shadow * (vec3(rho_d) * cosine + rho_s * cosine2), 0.0);
}
...
}
这个理解起来稍微麻烦些。对于遍历到的片元,我们首先要计算该片元处于shadowmap中的什么xy坐标上。具体方式就是将当前片元的世界坐标乘以lightSpaceMatrix,并按照流程作透视除法并映射到屏幕空间中,此时得到的x、y就是该片元在shadowMap中的采样坐标,采样得到的closestDepth就是光源向该片元方向打光,与第一个遮挡物体的距离是多少;而刚才得到的屏幕空间坐标下的z值就是当前片元在灯源视角下的实际深度值是多少。上述两个深度都是经过透视矩阵后的非线性深度,可以直接进行比较。

3、异常现象修正
①如上图所示,出现了很多令人san值狂掉小条纹,根本原因是深度纹理的像素有尺寸,采样率有限,所以地上有很多像素在深度纹理中采样到的深度值比实际距离要小了一点点,这样就被误判成了有阴影。所以这里我们需要加一个bias:
float bias = 0.005;
float shadow = currentDepth - bias > closestDepth ? 1.0 : 0.0;
这样我们就避免了黑色条纹:

考虑到性能问题,又考虑到shader中可以使用的纹理有限,我们不太能接收场景中有多个直接光,所以我们暂时只做单直接光的阴影即可。
②现在的阴影是悬浮和模型有脱节的部分,这是因为我们模型的”前面“计算出来的阴影偏移量太大,而如果我们只使用模型的”后面“计算,偏移量就会小很多。因此我们可以在计算深度纹理阶段剔除前面,保留后面:
glCullFace(GL_FRONT); ... glCullFace(GL_BACK);
现在还有一个需要修正的问题,那就是:由于深度纹理存储的像素个数有限,因此场景会有很多区域不在深度纹理的存储范围内。那么范围外的片元去采样深度纹理的时候,就会得到默认值0.0,这意味着该片元采样到的深度纹理深度永远小于实际距离,那么就一定会判断成阴影。事实上我们希望这种范围外的片元保留光亮度,所以我们可以给纹理边缘赋予一个白色(1.0),然后将纹理扩展格式改为GL_CLAMP_TO_BORDER:
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_BORDER);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_BORDER);
GLfloat borderColor[] = { 1.0, 1.0, 1.0, 1.0 };
glTexParameterfv(GL_TEXTURE_2D, GL_TEXTURE_BORDER_COLOR, borderColor);
4、PCF
PCF其实就是软阴影,让阴影的边缘更加柔和。之前我们在计算阴影的时候,直接采样深度纹理的对应像素的值来作对比;现在我们可以在深度纹理对应像素位置周围做一下”卷积“:
float cal_dir_shadow()
{
vec4 fragPosLightSpace = lightSpaceMatrix * vec4(f_FragPos,1.0);
// 执行透视除法
vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w;
// 变换到[0,1]的范围
projCoords = projCoords * 0.5 + 0.5;
// 取得当前片段在光源视角下的深度
float currentDepth = projCoords.z;
// 检查当前片段是否在阴影中
float bias = 0.005;
float shadow = 0.0;
vec2 texelSize = 1.0 / textureSize(shadowMap, 0);
for(int x = -1; x <= 1; ++x)
{
for(int y = -1; y <= 1; ++y)
{
float pcfDepth = texture(shadowMap, projCoords.xy + vec2(x, y) * texelSize).r;
shadow += currentDepth - bias > pcfDepth ? 1.0 : 0.0;
}
}
shadow /= 9.0;
return shadow;
}
这样阴影边缘就会柔和一些了:
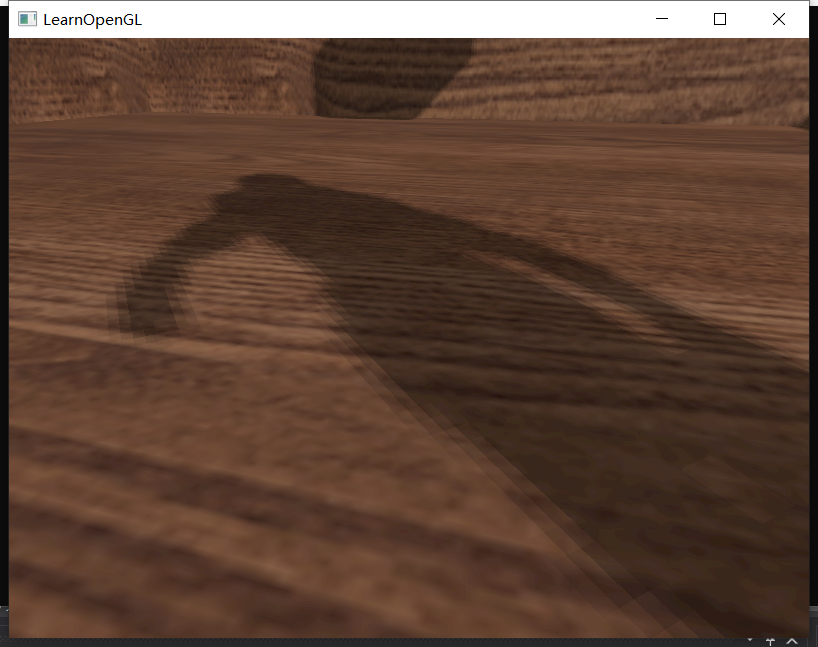
现在平行光的阴影就处理到位了,接下来我们考虑一下点光源的阴影。
Part4. 点光源阴影
点光源的阴影相对而言会复杂很多,因为它的光照方向是四面八方的,因此一张平坦的纹理没有办法将各个方向的深度信息都记载完成。如果我们想描述四面八方各个区域的深度信息,就只能使用包含了六张子纹理的立方体贴图:
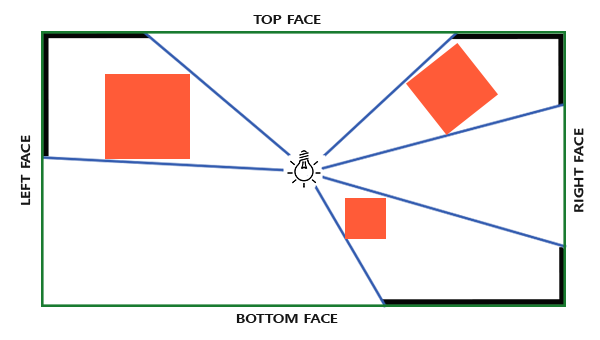
如图所示,空间中心有一个光源,它向周围每一个方向发射的光线都可以被立方体贴图所捕获。这也意味着,在光源视角捕捉深度的时候,需要一下子捕捉6个角度的结果。
1、深度缓冲与贴图绑定
与直接光的绑定大同小异,不过这次我们要绑定的是立方体贴图:
/*点光源阴影缓冲设置*/
GLuint depthMapFBO2;
glGenFramebuffers(1, &depthMapFBO2);
/*点光源阴影纹理设置*/
GLuint depthCubemap;
glGenTextures(1, &depthCubemap);
const GLuint SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024;
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
for (GLuint i = 0; i < 6; ++i)
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_DEPTH_COMPONENT,
SHADOW_WIDTH, SHADOW_HEIGHT, 0, GL_DEPTH_COMPONENT, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO2);
glFramebufferTexture(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, depthCubemap, 0);
glDrawBuffer(GL_NONE);
glReadBuffer(GL_NONE);
glBindFramebuffer(GL_FRAMEBUFFER, 0);
然后我们开始向shader中传送数据。因为点光源是发散型的灯光,所以这次不能再使用正交矩阵了,而是使用透视矩阵;同时我们还需要向6个方向分别透射视角:
/////////////////////////这里开始点光源视角渲染
shader_point_light.use();
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO2);
glClear(GL_DEPTH_BUFFER_BIT);
GLfloat aspect = (GLfloat)SHADOW_WIDTH / (GLfloat)SHADOW_HEIGHT;
GLfloat near = 1.0f;
GLfloat far = 50.0f;
glm::mat4 shadowProj = glm::perspective(glm::radians(90.0f), aspect, near, far);
std::vector<glm::mat4> shadowTransforms;
shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3(1.0, 0.0, 0.0), glm::vec3(0.0, -1.0, 0.0)));
shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3(-1.0, 0.0, 0.0), glm::vec3(0.0, -1.0, 0.0)));
shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3(0.0, 1.0, 0.0), glm::vec3(0.0, 0.0, 1.0)));
shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3(0.0, -1.0, 0.0), glm::vec3(0.0, 0.0, -1.0)));
shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3(0.0, 0.0, 1.0), glm::vec3(0.0, -1.0, 0.0)));
shadowTransforms.push_back(shadowProj * glm::lookAt(lightPos, lightPos + glm::vec3(0.0, 0.0, -1.0), glm::vec3(0.0, -1.0, 0.0)));
for (GLuint i = 0; i < 6; ++i)
shader_point_light.setMatrix("shadowMatrices[" + std::to_string(i) + "]", shadowTransforms[i]);
shader_point_light.setFloat("far_plane", far);
shader_dir_light.setMatrix("model", model);
models->Draw(shader_point_light);
glBindFramebuffer(GL_FRAMEBUFFER, 0);
这里我们的透视矩阵的张角必须是90°,这样6个方向才能正好包络住一个封闭的场景。然后我们将这6个透视矩阵传入shader中。
接下来我们来看着色器。首先顶点着色器非常简单:
#version 330 core
layout (location = 0) in vec3 position;
uniform mat4 model;
void main()
{
gl_Position = model * vec4(position, 1.0);
}
按照直接光阴影的逻辑,我们应该让顶点着色器把顶点变换到投影空间下才对,为什么到点光源阴影这里就只变换到世界空间呢?这是因为我们要在vs和fs之间插入一个几何着色器,将顶点的世界坐标全部塞给几何着色器,它就可以同时计算出该顶点在6个方向投影下的投影坐标。这个相当精妙,相当于把原本要做6次渲染的事情改成了1次渲染完成!
几何着色器这样写:
#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices=18) out;
uniform mat4 shadowMatrices[6];
out vec4 FragPos; // FragPos from GS (output per emitvertex)
void main()
{
for(int face = 0; face < 6; ++face)
{
gl_Layer = face; // built-in variable that specifies to which face we render.
for(int i = 0; i < 3; ++i) // for each triangle's vertices
{
FragPos = gl_in[i].gl_Position;
gl_Position = shadowMatrices[face] * FragPos;
EmitVertex();
}
EndPrimitive();
}
}
这里有一个很关键的内建变量,叫做gl_Layer,它决定了我们接下来发射的新顶点会发送到立方体贴图的哪个面上。首先我们拿到一组三角面元,然后分别计算三角形上三个顶点 在六个方向上的透视坐标,最后发射新顶点到对应方向的面上去。
那么我们的片元着色器只需要人为计算一下深度就好了:
#version 330 core
in vec4 FragPos;
uniform vec3 lightPos;
uniform float far_plane;
void main()
{
float lightDistance = length(FragPos.xyz - lightPos);
lightDistance = lightDistance / far_plane;
gl_FragDepth = lightDistance;
}
为什么这里要人为计算深度呢,因为我们之前用透视矩阵做完变换后的深度是非线性的,我们不希望使用如此意义不明的非线性深度值,所以要人为定义:世界空间下的距离直接作为深度。
2、正经渲染时采样深度纹理
现在我们得到了六张深度纹理,这张纹理送入到我们的普通shader中去做采样。普通shader的片元着色器作如下修改:
uniform sampler2D dir_shadowMap;
uniform samplerCube point_shadowMap;
uniform float far_plane;
...
float cal_point_shadow()
{
vec3 fragToLight = f_FragPos - pl[0].pos;
float closestDepth = texture(point_shadowMap, fragToLight).r;
closestDepth *= far_plane;
float currentDepth = length(fragToLight);
float bias = 15.0;
float shadow = currentDepth - bias > closestDepth ? 1.0 : 0.0;
return shadow;
}
...
for(int i = 0; i < 1; i++){
if(pl[i].color == vec3(0,0,0)) continue;
vec3 lightDir = normalize(pl[i].pos - f_FragPos);
vec3 h = (lightDir + viewDir) / length(lightDir + viewDir);
float distance = length(pl[i].pos - f_FragPos);
float cosine = max(dot(norm, lightDir), 0.0);
vec3 reflectDir = reflect(-lightDir, norm);
float cosine2 = pow(max(dot(norm, h), 0.0), material.shininess_n);
vec3 pl_color = pl[i].color / (pl[i].constant + pl[i].linear * distance + pl[i].quadratic * distance * distance);
float shadow = cal_point_shadow();
FragColor += vec4(pl_color * (1 - shadow) * (vec3(rho_d) * cosine + rho_s * cosine2), 0.0);
}
这样就完成了对shadowmap的采样和距离对比,从而刻画出点光源的阴影了。但是我这里的bias大的惊人,居然达到了15.0,我分析了一下感觉和far_plane的数量级有关。当far_plane数量级较大的时候,深度纹理中存储的数据丢失精度更严重,所以这个时候需要补偿的bias也就越大。
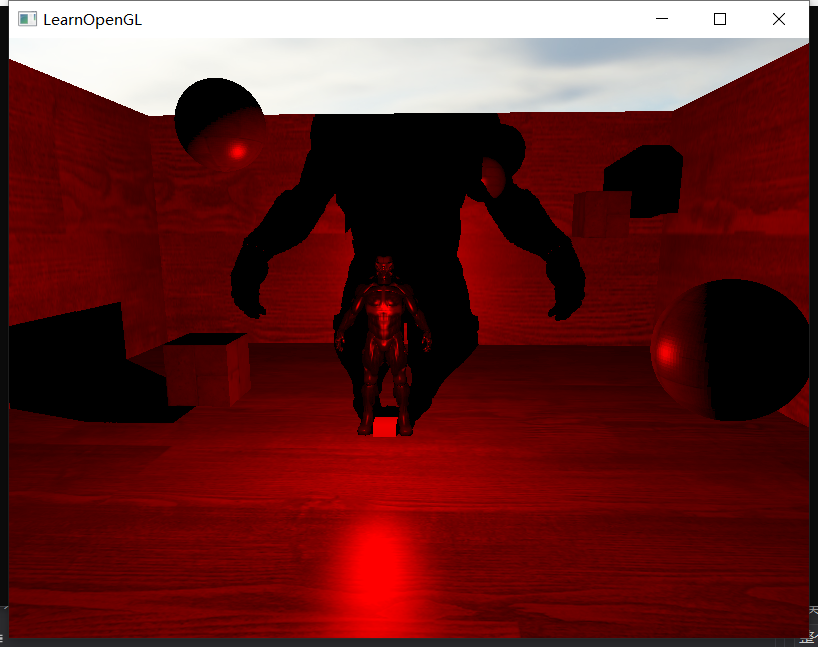
3、PCF
原理与直接光的PCF原理类似,只不过采样的方法改了:
vec3 sampleOffsetDirections[20] = vec3[]
(
vec3( 1, 1, 1), vec3( 1, -1, 1), vec3(-1, -1, 1), vec3(-1, 1, 1),
vec3( 1, 1, -1), vec3( 1, -1, -1), vec3(-1, -1, -1), vec3(-1, 1, -1),
vec3( 1, 1, 0), vec3( 1, -1, 0), vec3(-1, -1, 0), vec3(-1, 1, 0),
vec3( 1, 0, 1), vec3(-1, 0, 1), vec3( 1, 0, -1), vec3(-1, 0, -1),
vec3( 0, 1, 1), vec3( 0, -1, 1), vec3( 0, -1, -1), vec3( 0, 1, -1)
);
...
float shadow = 0.0;
float bias = 0.15;
int samples = 20;
float viewDistance = length(viewPos - fragPos);
float diskRadius = 0.05;
for(int i = 0; i < samples; ++i)
{
float closestDepth = texture(depthMap, fragToLight + sampleOffsetDirections[i] * diskRadius).r;
closestDepth *= far_plane; // Undo mapping [0;1]
if(currentDepth - bias > closestDepth)
shadow += 1.0;
}
shadow /= float(samples);
除此之外还可以做一点优化,我们可以基于相机到fragment的距离来改变diskRadius;这样我们就能根据观察者的距离来增加偏移半径了,当距离更远的时候阴影更柔和,更近了就更锐利:
float viewDistance = length(cameraPos - f_FragPos);
float diskRadius = (1.0 + (viewDistance / far_plane)) / 2.0;
这样阴影就相当柔和且自然了:
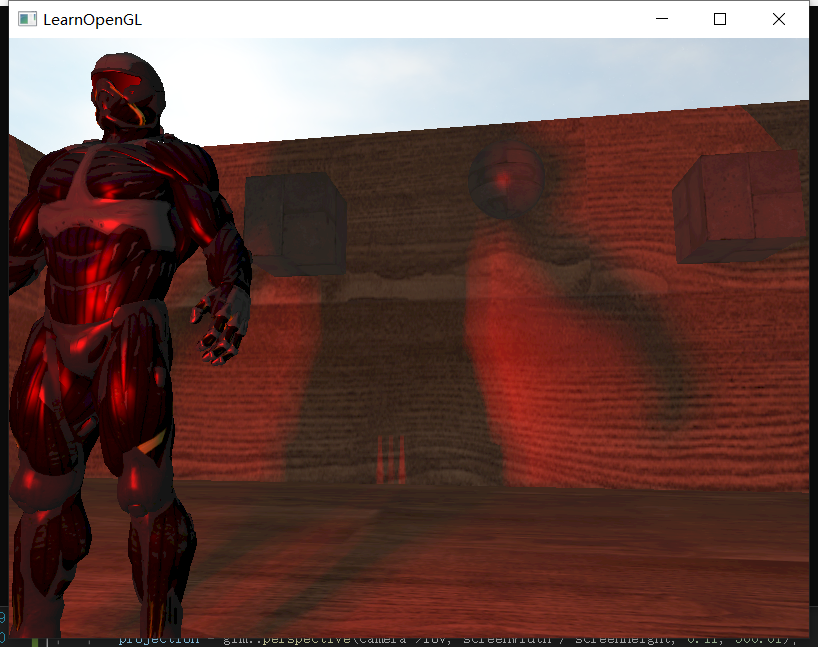
现在我们将点光源和直接光源同时加上,并让他们同时产生阴影,效果如下:

效果还可以,不过实话说,当灯的数量>1时,阴影就开始比较凌乱了。所以考虑场景整洁度+性能,我们最多只让1个直接光+1个点光源产生阴影即可,其他的副光源就先不要产生阴影了。(真实原因:懒)
Part5. 法线与法线贴图
终于到法线贴图这一节了。回首我之前写过的三个渲染器,似乎都还没有引入法线贴图的功能,有点遗憾。
在制作模型并导出的时候,每个顶点都会有一个法线信息,当我们使用opengl渲染时,在光栅化阶段,管线会对每个三角形三个顶点的法线作插值,来计算三角形内每个片元的法线值。这个是大家早已熟知的事情。
不过在制作模型的时候,会有一点分歧。如果我们开启的是“平直着色”,那么对于每一个三角形的顶点,其法线方向都与当前三角面的法线方向相同。假如某一个顶点P同时作为A、B两个三角面的公用顶点,那么当P作为A面顶点时,P的法线与A面法线相同;P作为B面顶点时,P的法线与B面法线相同,这意味着P点同时拥有两个完全不同方向的法线(即法线发生突变),那么A和B的交界处就会产生突变:

所以我们可以在建模软件中开启另一种着色,叫“平滑着色”。假如某一个顶点P同时作为A、B两个三角面的公用顶点,那么P点在两个面中的法线强行置为两个三角面法线的均值,这样P点自身就不会再发生突变了,而是给予了一个过渡的桥梁,此时三角面内的片元再做插值,就可以得到圆滑的法线方向了:

所以不同的着色模型决定了每个顶点在三角形内的法线方案。然而这些法线方案本质上都是根据模型的顶点、三角面等图元信息计算出来的,并不能自己定制法线方向。那么如何自定义每个片元的法线信息呢?这就需要我们的法线贴图出马了。
法线贴图就声明了每一个片元在其切线空间下的法线方向。什么是切线空间呢,就是以三角面u方向为空间切线(x轴)、以v方向为空间副切线(y轴)、以法线为空间法线(z轴)的空间。使用切线空间本质上是在简化问题:我不管你这个三角面现在朝向哪个方向,我这张贴图只描述三角面竖直朝上时,各个片元的自定义法线方向是什么。如果想得到这些自定义法线在世界空间中的方向,那等采样完成后再后期做一次空间变换就好了。
1、如何将法线从切线空间变换到世界空间?
在切线空间中,切线T轴的轴向量是(1,0,0),副切线B轴的轴向量是(0,1,0),法线N轴的轴向量是(0,0,1)。在切线空间下某个向量V的值为(a,b,c),意味着:
$$V = a * T + b * B + c * N$$
现在我们要想求V在世界空间中的向量表示,其实就是:
$$V_世 = a * T_世 + b * B_世 + c * N_世$$
所以我们本质上需要得到T、B、N三个轴在世界空间下的向量表示。
2、如何求TBN三个轴向量在世界空间下的表示?
如图所示,假设P1、P2、P3是三个顶点在世界空间下的坐标:
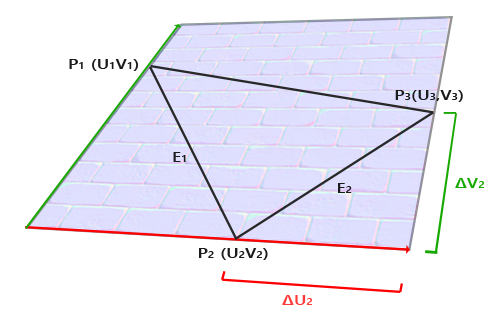
我们假设左下角的原点为O,那我们可以得到以下式子:
$$OP_1 = U_1 * T + V_1 * B$$
$$OP_2 = U_2 * T + V_2 * B$$
$$OP_3 = U_3 * T + V_3 * B$$
由于E1 = P2 – P1,E2 = P3 – P2,所以:
$$E_1 = P_1P_2 = (U_2 – U_1) * T + (V_2 – V_1) * B$$
$$E_2 = P_2P_3 = (U_3 – U_2) * T + (V_3 – V_2) * B$$
然后我们解这个式子就可以了。这相当于6元一次方程式,直接硬解比较麻烦,可以将其转换为矩阵乘法的形式:

不知道怎么用mathjax写矩阵,所以直接粘贴learnOpengl的截图了。。。
通过这个公式,我们就可以得到T、B、N在世界空间下的向量表示了,那么我们就可以求出切线空间下的法线在世界空间中的坐标了。
3、在哪个阶段做TBN计算?
根据上文的推导,当我们拿到了三角形三个顶点在世界空间下的坐标以及uv后,可以将其放入几何着色器中计算TBN(因为几何着色器能拿到完整三角面元,可以获得三个顶点的uv值和世界坐标)这确实是一种可行的方法。
但是一定要放到几何着色器来做吗?我们想一下,是否可以在模型导入的时候,就给每个顶点计算好模型空间下的TBN,然后在顶点着色器中给这个TBN乘一个模型-世界变换矩阵,这样也可以得到世界空间下的TBN。而且这样做的好处是,首先不需要几何着色器了,其次可以将计算TBN的主要任务放在模型导入期,而不需要在渲染的时候一直去反复算。
恰好assimp给予了接口,可以直接在导入模型的时候将每个顶点在模型空间下的切线和副切线全部计算出来。
myModel.h:
if (mesh->HasNormals())
{
vector.x = mesh->mNormals[i].x;
vector.y = mesh->mNormals[i].y;
vector.z = mesh->mNormals[i].z;
vertex.normal = vector;
vector.x = mesh->mTangents[i].x;
vector.y = mesh->mTangents[i].y;
vector.z = mesh->mTangents[i].z;
vertex.tangent = vector;
vector.x = mesh->mBitangents[i].x;
vector.y = mesh->mBitangents[i].y;
vector.z = mesh->mBitangents[i].z;
vertex.bitangent = vector;
}
在myMesh.h的setup方法中,将切线和副切线一起载入:
// 顶点位置 glEnableVertexAttribArray(0); glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, sizeof(vertice), (void*)0); // 顶点纹理坐标 glEnableVertexAttribArray(1); glVertexAttribPointer(1, 2, GL_FLOAT, GL_FALSE, sizeof(vertice), (void*)offsetof(vertice, uv)); // 顶点法线 glEnableVertexAttribArray(2); glVertexAttribPointer(2, 3, GL_FLOAT, GL_FALSE, sizeof(vertice), (void*)offsetof(vertice, normal)); // 顶点切线 glEnableVertexAttribArray(3); glVertexAttribPointer(3, 3, GL_FLOAT, GL_FALSE, sizeof(vertice), (void*)offsetof(vertice, tangent)); // 顶点副切线 glEnableVertexAttribArray(4); glVertexAttribPointer(4, 3, GL_FLOAT, GL_FALSE, sizeof(vertice), (void*)offsetof(vertice, bitangent));
这样在顶点着色器中,我们可以直接得到当前顶点在模型空间下的切线和副切线,然后我们给T、B、N乘一个model矩阵,便得到了切线空间->世界空间的转换矩阵。
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aUV;
layout (location = 2) in vec3 aNormal;
layout (location = 3) in vec3 aTangent;
layout (location = 4) in vec3 aBitangent;
out VS_OUT {
vec3 normal;
vec2 texcoord;
vec3 FragPos;
mat3 TBN;
}vs_out;
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;
void main()
{
gl_Position = projection * view * model * vec4(aPos, 1.0);
vs_out.FragPos = vec3(model * vec4(aPos, 1.0));
vs_out.normal = mat3(transpose(inverse(model))) * aNormal;;
vs_out.texcoord = aUV;
vec3 T = normalize(vec3(model * vec4(aTangent, 0.0)));
vec3 B = normalize(vec3(model * vec4(aBitangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0)));
vs_out.TBN = mat3(T, B, N);
}
将TBN传递给几何着色器,再传递到片元着色器中:
#version 330 core
in mat3 f_TBN;
...
struct Material {
vec3 ambient;
vec4 diffuse;
bool diffuse_texture_use;
sampler2D diffuse_texture;
vec3 specular;
bool specular_texture_use;
sampler2D specular_texture;
float reflects;
bool reflect_texture_use;
sampler2D reflect_texture;
bool normal_texture_use;
sampler2D normal_texture;
float shininess_n;
};
...
void main()
{
vec3 norm = normalize(f_normal);
if(material.normal_texture_use == true) {
norm = texture(material.normal_texture, f_texcoord).rgb;
norm = normalize(norm * 2.0 - 1.0);
norm = normalize(f_TBN * norm);
}
...
这样我们就成功将法线贴图上的法线转换成世界法线来用了:
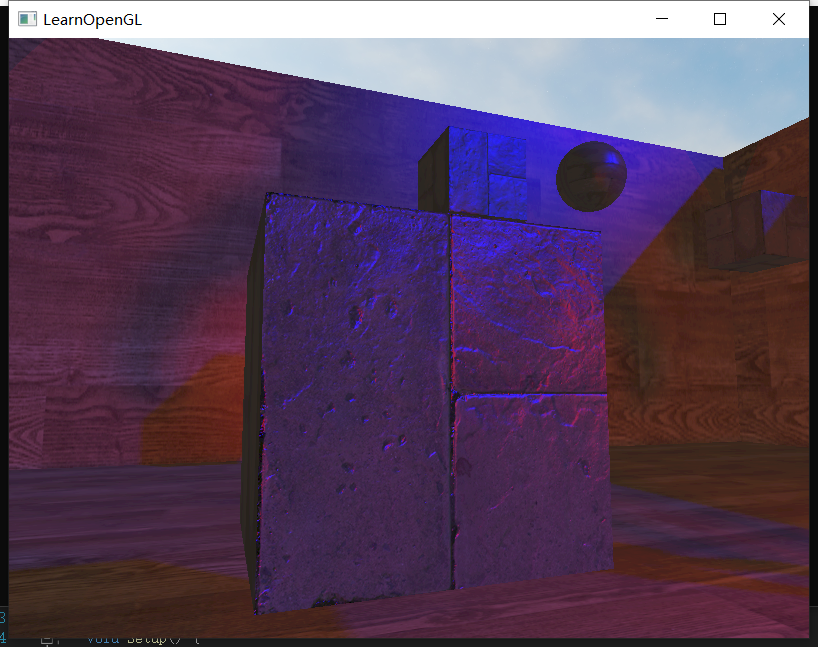
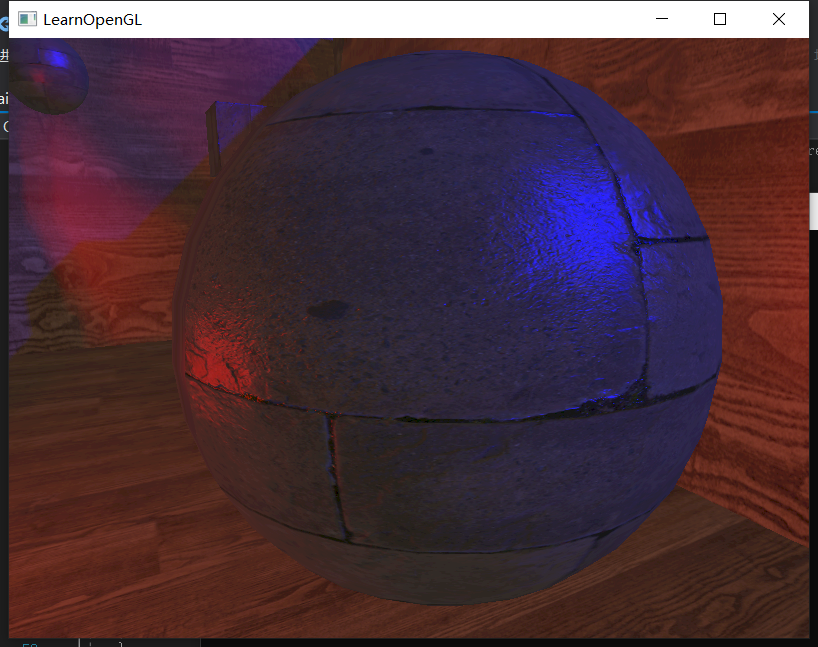
有一说一,好使!
然而这里又埋藏了一个坑。还记得在这个Part开头我们提到过“平直着色”和“平滑着色”吗?如果我们模型使用的是平直着色,那其实没有任何问题;但是如果我们模型使用的是平滑着色,那么此时某个共享顶点的法线将被“平均化”,此时的TBN很有可能不再互相垂直了,我们称之为非正交关系。
TBN互相正交是非常重要的,因为我们的模型空间的三个维度是正交的,世界空间的三个维度也是正交的,如果变换后的TBN空间不再正交,后续的计算就会出现很多错误。所以我们要在顶点着色器阶段制作TBN前,对T、B、N做一次施密特正交化:
vec3 T = normalize(vec3(model * vec4(aTangent, 0.0))); vec3 N = normalize(vec3(model * vec4(aNormal, 0.0))); T = normalize(T - dot(T, N) * N); vec3 B = cross(T, N); vs_out.TBN = mat3(T, B, N);
这样就可以保证,使用“平滑着色”的模型顶点也可以拥有正交的TBN。
本来应该在下一个part复现视差贴图的,但是现在视差贴图的应用范围并不太广,而且视差贴图的资源也不好找,所以这一节先跳过。
Part6. HDR
现在我们场景的色彩范围其实很窄,rgb的范围都是(0,1),现在我们希望场景能够储存更广的范围数值(例如rgb都>1),我们就需要将纹理的格式改为:
//glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, screenWidth, screenHeight, 0, GL_RGB, GL_UNSIGNED_BYTE, NULL);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, screenWidth, screenHeight, 0, GL_RGB, GL_FLOAT, NULL);
RGB16F可以存储>1的颜色值。当我们获得这种超出范围的颜色后,我们可以调整一下它的曝光量再输出。
第一种方式是自动调整曝光,将场景的rgb直接映射到(0,1)之间,我们可以在后处理shader的片元着色器中这样写:
vec3 mapped = colors / (colors + vec3(1.0));
FragColor.rgb = pow(mapped,vec3(1/2.2));
FragColor.a = 1.0;
当然有时候我们希望自己可以手动调整曝光量,一般遵循这样的公式:
$$rgb_{tonemap} = 1 – e^{\frac{-p * rgb}{q}}$$
p和q都是与曝光变化相关的参数。那么片元着色器可以这样写:
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
uniform sampler2D screenTexture;
uniform float exposure;
void main()
{
vec3 colors = vec3(texture(screenTexture, TexCoords));
//这里对colors进行后处理
vec3 mapped = vec3(1.0) - exp(-colors * exposure);
FragColor.rgb = pow(mapped,vec3(1/2.2));
FragColor.a = 1.0;
}
通过exposure来调整曝光,默认为1,调大后亮度整体放大,调小后亮度整体变小。
Part7. 泛光效果
炫光效果的逻辑如图:
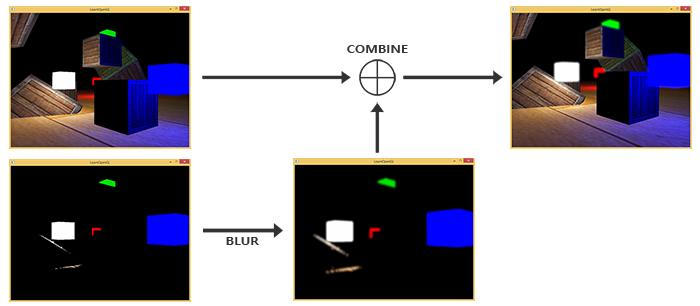
所以流程就是,当我们渲染场景时,需要将结果写入两张纹理a和b中;b要用bloom shader做一次阈值剔除+高斯模糊,然后将两者的结果加在一起即可。
首先是申请两个帧缓冲纹理:
/*帧缓冲设置*/
unsigned int framebuffer;
glGenFramebuffers(1, &framebuffer);
glBindFramebuffer(GL_FRAMEBUFFER, framebuffer);
/*帧纹理设置,将帧缓冲的颜色信息写入*/
unsigned int textureColorbuffer[2];
glGenTextures(2, textureColorbuffer);
for (unsigned int i = 0; i < 2; i++) {
glBindTexture(GL_TEXTURE_2D, textureColorbuffer[i]);
//glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, screenWidth, screenHeight, 0, GL_RGB, GL_UNSIGNED_BYTE, NULL);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, screenWidth, screenHeight, 0, GL_RGB, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0 + i, GL_TEXTURE_2D, textureColorbuffer[i], 0);
}
GLuint attachments[2] = { GL_COLOR_ATTACHMENT0, GL_COLOR_ATTACHMENT1 };
glDrawBuffers(2, attachments);
这里我们必须用glDrawBuffers来绑定两个输出纹理,这样我们在片元着色器可以分别写入,对于第一张纹理我们直接写入普通结果就好了,而对于第二章纹理我们要做一下阈值剔除:
#version 330 core
layout (location = 0) out vec4 FragColor;
layout (location = 1) out vec4 BrightColor;
...
void main()
{
vec3 norm = normalize(f_normal);
...
FragColor.rgb = environment * rho_r + FragColor.rgb * (1 - rho_r);
//FragColor.a = rho_d.a;
float brightness = dot(FragColor.rgb, vec3(0.2126, 0.7152, 0.0722));
if(brightness > 1.0)
BrightColor = vec4(FragColor.rgb, 1.0);
}
这样我们就完成了两张纹理的写入。接下来我们要对二号纹理进行高斯模糊,一共需要绑定两个高斯模糊的纹理,分别装载横向卷积和纵向卷积的结果。具体流程就是一遍横向卷积、一遍纵向卷积、再一遍横向卷积……
GLuint pingpongFBO[2];
GLuint pingpongBuffer[2];
glGenFramebuffers(2, pingpongFBO);
glGenTextures(2, pingpongBuffer);
for (GLuint i = 0; i < 2; i++)
{
glBindFramebuffer(GL_FRAMEBUFFER, pingpongFBO[i]);
glBindTexture(GL_TEXTURE_2D, pingpongBuffer[i]);
glTexImage2D(
GL_TEXTURE_2D, 0, GL_RGB16F, SCR_WIDTH, SCR_HEIGHT, 0, GL_RGB, GL_FLOAT, NULL
);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glFramebufferTexture2D(
GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, pingpongBuffer[i], 0
);
}
...
/*泛光*/
GLboolean horizontal = true, first_iteration = true;
GLuint amount = 10;
shader_bloom.use();
for (GLuint i = 0; i < amount; i++)
{
glBindFramebuffer(GL_FRAMEBUFFER, pingpongFBO[horizontal]);
shader_bloom.setBool("horizontal", horizontal);
glBindTexture(GL_TEXTURE_2D, first_iteration ? textureColorbuffer[1] : pingpongBuffer[!horizontal]);
glBindVertexArray(quadVAO);
glDrawArrays(GL_TRIANGLES, 0, 6);
horizontal = !horizontal;
if (first_iteration)
first_iteration = false;
}
具体bloom的片元着色器就需要进行卷积操作,不断取样当前纹理周围的纹理进行卷积模糊,注意横向和纵向必须是分开交错的:
#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
uniform sampler2D image;
uniform bool horizontal;
uniform float weight[5] = float[] (0.227027, 0.1945946, 0.1216216, 0.054054, 0.016216);
void main()
{
vec2 tex_offset = 1.0 / textureSize(image, 0); // gets size of single texel
vec3 result = texture(image, TexCoords).rgb * weight[0]; // current fragment's contribution
if(horizontal)
{
for(int i = 1; i < 5; ++i)
{
result += texture(image, TexCoords + vec2(tex_offset.x * i, 0.0)).rgb * weight[i];
result += texture(image, TexCoords - vec2(tex_offset.x * i, 0.0)).rgb * weight[i];
}
}
else
{
for(int i = 1; i < 5; ++i)
{
result += texture(image, TexCoords + vec2(0.0, tex_offset.y * i)).rgb * weight[i];
result += texture(image, TexCoords - vec2(0.0, tex_offset.y * i)).rgb * weight[i];
}
}
FragColor = vec4(result, 1.0);
}
最后我们就得到了高斯模糊后的纹理缓冲,将其送入后处理的shader片元着色器进行混合:
void main()
{
vec3 colors = vec3(texture(screenTexture, TexCoords));
vec3 bloomColor = texture(bloomTexture, TexCoords).rgb;
colors += bloomColor;
//这里对colors进行后处理
vec3 mapped = vec3(1.0) - exp(-colors * exposure);
FragColor.rgb = pow(mapped,vec3(1/2.2));
FragColor.a = 1.0;
}
这样我们就将泛光部分添加回原来的输出结果上了。
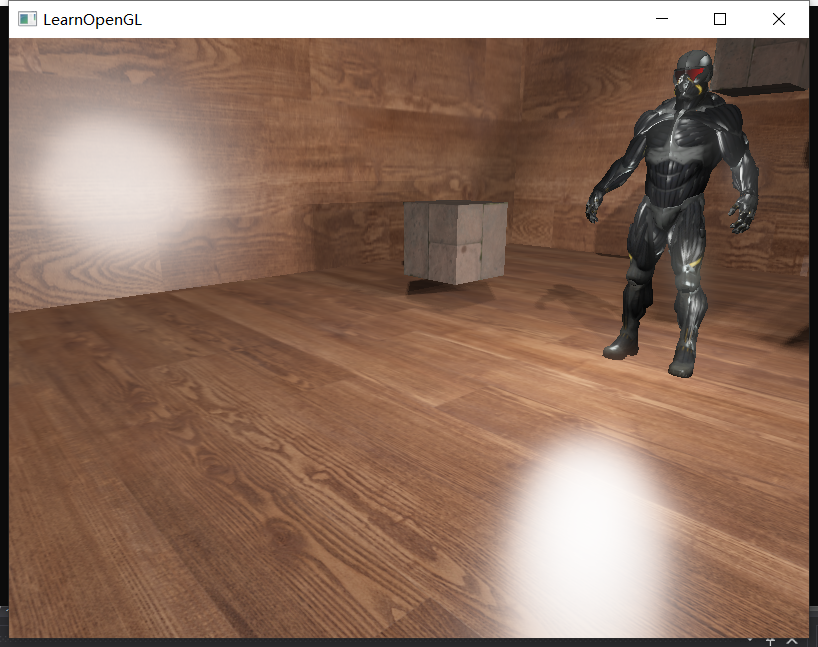
可以看到人物的大腿、地板的反光都有种泛光的感觉了。效果其实不算很明显,然而性能掉的是真严重啊……有点得不偿失的感觉了。
延迟着色和SSAO属于是难度较大、文章篇幅较长的技术点,我准备放在日后单独开一篇blog来讲。