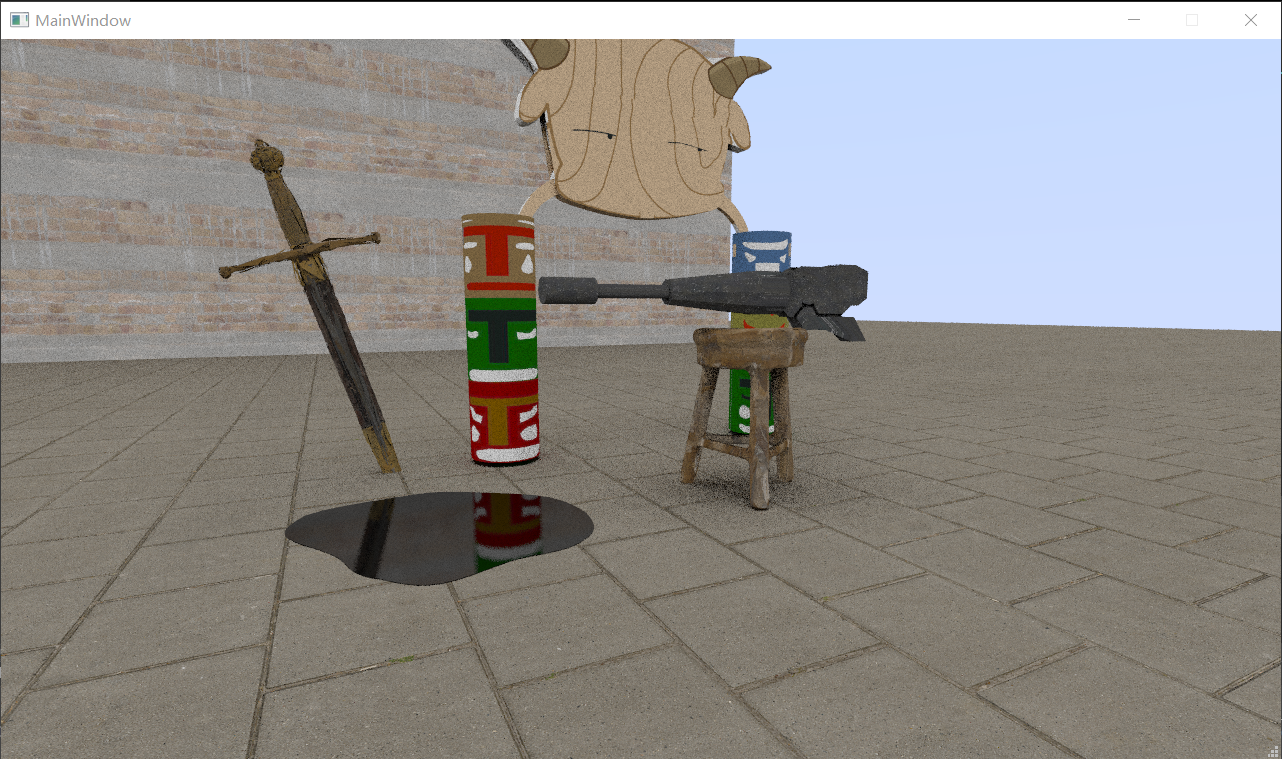
C++光线追踪渲染器终结版
- 23 11 月, 2021
- by
- pladmin
引言
上一篇博客实现了光线追踪所需要的绝大部分功能,例如模型导入、贴图映射、场景光源等,我们也可以渲染各种各样想要的场景效果了。但是现在仍然存在两个优化问题:一是渲染效率太低,二是渲染噪点压不下去。所以在光线追踪渲染器的收尾篇,我们重点讨论解决这两个问题所使用的方法:BVH优化、基于重要性采样的蒙特卡洛路径追踪。
BVH优化
BVH盒全称是Bounding Volume Hierarchies,即层次包围盒。这里我们先不直接讲它的原理,我们先来回忆一下之前的内容:当我们要开始求交的时候,我们需要拿到hittable_list,然后逐个遍历每个物体。这样我们的求交复杂度是O(n),当场景较为庞大,三角面的数量达到十万、百万级别的时候,求交会变成一个极其吃力的事情。因此,我们需要将求交的复杂度进一步降低。
具体怎么降低呢?我们要将原来线性排列的所有hittable物体转变成二叉树的结构,这样在最理想的情况下可以将时间复杂度从O(n)降到O(logn)。
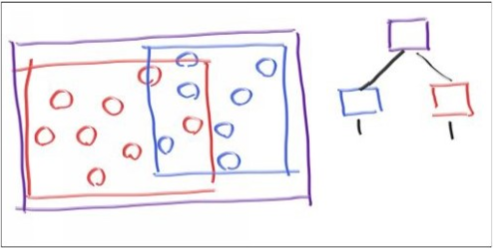
如上图所示,我们将所有hittable物体按空间关系划分为了左右两部分,每部分被一个包围盒所包含。当我们开始进行光线求交时,我们不直接用具体的球或三角形逐个测试,而是先和这两个包围盒进行求交,如果某个包围盒测试的结果是不能与光线相交,那么其包围的所有物体将全部淘汰。而对于相交成功的包围盒,其也会包含两个包围盒,重复上述步骤,迭代到最后一轮的包围盒内只有一个物体,那么光线与该物体进行求交即可。
现在大家已经了解了BVH的工作原理了。所以我来整理一下使用BVH算法的全部流程:1、将所有hittable物体按坐标排序,具体到底是按哪个轴的坐标排序是随机选的(可能大家对每次随机选轴有疑问,不过不要紧,最后我会展示随机选和不随机选在效率上的区别);2、将所有物体按照排序结果平分为两部分(即两个子节点),各自的部分再排序,仍然是随机选轴;3、持续步骤2进行递归,直到节点内只包含1个物体,此时计算这个物体的包围盒;4、开始回溯,父节点根据两个子节点的包围盒来计算自己的包围盒,要保证自己的包围盒能够紧密涵盖两个子物体的包围盒;5、持续步骤4进行回溯,直到根节点的包围盒也计算完毕,此时结束BVH树的构建;6、开始求交时,直接对根节点的包围盒进行求交,成功则继续对两个子节点进行递归;7、重复步骤6,若最后求交到了具体的三角形和球体,则进行光线信息的计算和更新,若在某一层与所有包围盒都求交失败,则返回false。
根据上面的思路,我们需要两个新的类:aabb类(包围盒)和bvh_node(二叉树节点)。aabb主要是用于求交,bvh_node主要是用于搜索。
aabb类就是我们的包围盒,全称是Axis-aligned bounding box,它最大的特点就是轴对齐——即这个盒子的长宽高三个方向刚好对齐了世界空间的x、y、z方向,这样降低了问题难度。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 | #ifndef AABB_H #define AABB_H #include"rtweekend.h" #include"vec3.h" #include"ray.h" class aabb { public: aabb(){} aabb(const vec3& a, const vec3& b); inline bool hit(const ray& sight, double tmin, double tmax)const; static aabb _surrounding_box(aabb box1, aabb box2) { auto fmin = [](const double a, const double b) {return a < b ? a : b; }; auto fmax = [](const double a, const double b) {return a > b ? a : b; }; vec3 min{ fmin(box1.min().x(),box2.min().x()), fmin(box1.min().y(),box2.min().y()), fmin(box1.min().z(),box2.min().z()) }; vec3 max{ fmax(box1.max().x(),box2.max().x()), fmax(box1.max().y(),box2.max().y()), fmax(box1.max().z(),box2.max().z()) }; return aabb(min, max); } public: inline vec3 min()const { return _min; } inline vec3 max()const { return _max; } private: vec3 _min; vec3 _max; }; inline aabb::aabb(const vec3& a, const vec3& b):_min(a), _max(b){} bool aabb::hit(const ray& sight, double tmin, double tmax)const { double ox = sight.origin().x();double oy = sight.origin().y();double oz = sight.origin().z(); double dx = sight.direction().x();double dy = sight.direction().y();double dz = sight.direction().z(); double tx_min,ty_min,tz_min; double tx_max,ty_max,tz_max; //x0,y0,z0为包围体的最小顶点 //x1,y1,z1为包围体的最大顶点 double x0=min().x(),y0=min().y(),z0=min().z(); double x1=max().x(),y1=max().y(),z1=max().z(); if(fabs(dx) < 0.000001f) { //若射线方向矢量的x轴分量为0且原点不在盒体内 if(ox < x1 || ox > x0) return false ; } else { if(dx>=0) { tx_min = (x0-ox)/dx; tx_max = (x1-ox)/dx; } else { tx_min = (x1-ox)/dx; tx_max = (x0-ox)/dx; } } if(fabs(dy) < 0.000001f) { //若射线方向矢量的x轴分量为0且原点不在盒体内 if(oy < y1 || oy > y0) return false ; } else { if(dy>=0) { ty_min = (y0-oy)/dy; ty_max = (y1-oy)/dy; } else { ty_min = (y1-oy)/dy; ty_max = (y0-oy)/dy; } } if(fabs(dz) < 0.000001f) { //若射线方向矢量的x轴分量为0且原点不在盒体内 if(oz < z1 || oz > z0) return false ; } else { if(dz>=0) { tz_min = (z0-oz)/dz; tz_max = (z1-oz)/dz; } else { tz_min = (z1-oz)/dz; tz_max = (z0-oz)/dz; } } double t0,t1; //光线进入平面处(最靠近的平面)的最大t值 t0=maxd(tz_min,maxd(tx_min,ty_min)); //光线离开平面处(最远离的平面)的最小t值 t1=mind(tz_max,mind(tx_max,ty_max)); return t0<t1; } #endif // AABB_H |
代码其实不难理解。aabb盒无非要干的就这几件事:如何初始化aabb;当我得到两个子物体的包围盒时,作为父节点的aabb应该如何定义;光线与aabb如何求交。最后一件事相对比较难,对应的就是代码的hit函数。图像解释如下:
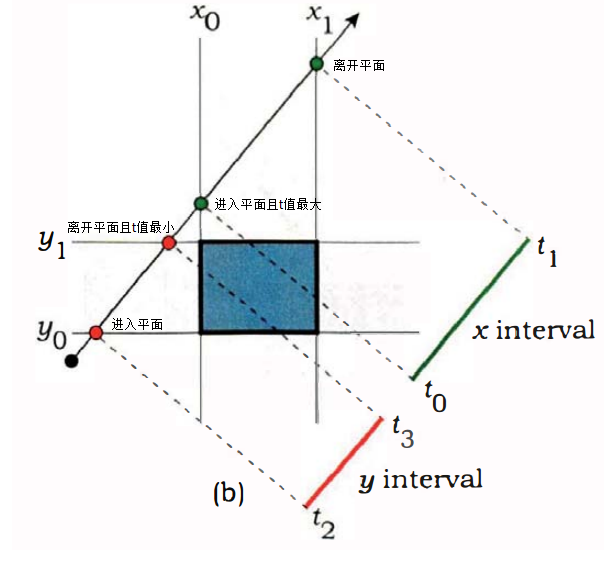
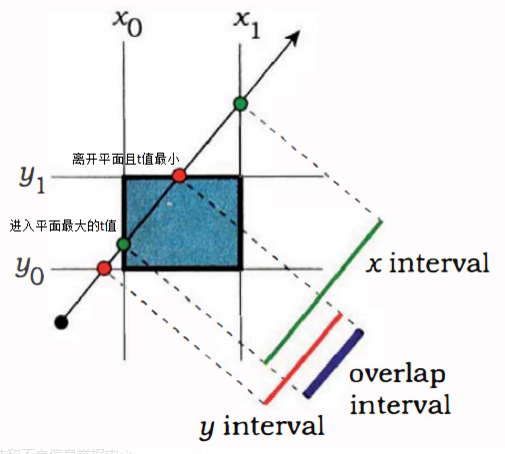
对于这个求交算法感兴趣的同学可以看一下(40条消息) 光线与包围盒(AABB)的相交检测算法_计算机图形编程-CSDN博客,讲的非常好。同时不要忘了,我们还要分别给出三角形和球体组织aabb盒的算法。我们知道aabb盒是一个长方体,它只需要两个向量max_xyz和min_xyz就能决定。对于球体而言,aabb盒的min_xyz就是球心坐标-半径,max_xyz就是球心坐标+半径;对于三角形而言,只要把三个点的最大x、y、z和最小x、y、z拉出来作max_xyz和min_xyz即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | aabb getbox() const override{ return aabb(center - vec3(radius, radius, radius), center + vec3(radius, radius, radius)); } aabb getbox() const override{ vec3 small( mind(pt[0].x(),mind(pt[1].x(),pt[2].x()))-0.0001, mind(pt[0].y(),mind(pt[1].y(),pt[2].y()))-0.0001, mind(pt[0].z(),mind(pt[1].z(),pt[2].z()))-0.0001 ); vec3 big( maxd(pt[0].x(),maxd(pt[1].x(),pt[2].x()))+0.0001, maxd(pt[0].y(),maxd(pt[1].y(),pt[2].y()))+0.0001, maxd(pt[0].z(),maxd(pt[1].z(),pt[2].z()))+0.0001 ); return aabb(small,big); } |
aabb盒就设计好了。接下来我们要设计bvh_node,从而建立这棵二叉树:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | #ifndef BVH_NODE_H #define BVH_NODE_H #include"hittable.h" #include"aabb.h" class bvh_node :public hittable { public: bvh_node(){} bvh_node(hittable** world, const int n); virtual bool hit(const ray& sight, double t_min, double t_max, hit_record& info)const override; virtual aabb getbox()const override{ return _box; } private: hittable* _left; hittable* _right; aabb _box; }; #endif // BVH_NODE_H |
学过数据结构的同学肯定写过二叉搜索树的代码,这个bvh树就和二叉搜索树没什么区别,每个父节点都具备左右两个子节点,同时每个节点有一个描述自己的aabb包围盒。具体建树和求交的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 | #include"bvh_node.h" inline int _x_cmp(const void * lhs, const void * rhs) { hittable * lc = *(hittable**)lhs; hittable * rc = *(hittable**)rhs; aabb lbox = lc->getbox(); aabb rbox = rc->getbox(); if (lbox.min().x() - rbox.min().x() < 0.) return -1; else return 1; } inline int _y_cmp(const void * lhs, const void * rhs) { hittable * lc = *(hittable**)lhs; hittable * rc = *(hittable**)rhs; aabb lbox = lc->getbox(); aabb rbox = rc->getbox(); if (lbox.min().y() - rbox.min().y() < 0.) return -1; else return 1; } inline int _z_cmp(const void * lhs, const void * rhs) { hittable * lc = *(hittable**)lhs; hittable * rc = *(hittable**)rhs; aabb lbox = lc->getbox(); aabb rbox = rc->getbox(); if (lbox.min().z() - rbox.min().z() < 0.) return -1; else return 1; } bvh_node::bvh_node(hittable** world, const int n) { /*int axis = static_cast<int>(3 * random_double()); if (axis == 0) qsort(world, n, sizeof(hittable*), _x_cmp); else if (axis == 1) qsort(world, n, sizeof(hittable*), _y_cmp); else qsort(world, n, sizeof(hittable*), _z_cmp);*/ qsort(world, n, sizeof(hittable*), _z_cmp); if (n == 1) _left = _right = world[0]; else if (n == 2) _left = world[0], _right = world[1]; else _left = new bvh_node(world, n / 2), _right = new bvh_node(world + n / 2, n - n / 2); aabb lbox = _left->getbox(); aabb rbox = _right->getbox(); _box = aabb::_surrounding_box(lbox, rbox); } bool bvh_node::hit(const ray& sight, double t_min, double t_max, hit_record& info)const { if (_box.hit(sight, t_min, t_max)) { hit_record linfo, rinfo; bool lhit = _left->hit(sight, t_min, t_max, linfo); bool rhit = _right->hit(sight, t_min, t_max, rinfo); if (lhit && rhit) { if (linfo.t < rinfo.t) info = linfo; else info = rinfo; return true; } else if (lhit) { info = linfo; return true; } else if (rhit) { info = rinfo; return true; } else{ return false; } } else{ return false; } } |
先来说说建树操作。回想前面提到的BVH工作步骤:1、将所有hittable物体按坐标排序,具体到底是按哪个轴的坐标排序是随机选的;2、将所有物体按照排序结果平分为两部分(即两个子节点),各自的部分再排序,仍然是随机选轴;3、持续步骤2进行递归,直到节点内只包含1个物体,此时计算这个物体的包围盒;4、开始回溯,父节点根据两个子节点的包围盒来计算自己的包围盒,要保证自己的包围盒能够紧密涵盖两个子物体的包围盒;5、持续步骤4进行回溯,直到根节点的包围盒也计算完毕,此时结束BVH树的构建。
求交操作也是一个递归的过程。首先若自身的aabb盒都求交失败,则可以直接返回false;否则就对两个子节点进行递归的求交测试。递归的终点在三角形和球体上,此时便开始回溯。父节点需要根据两个子节点的求交信息来决定hit_record写入哪个,然后再回溯到上一层,以此类推,就完成了光线与场景物体的求交操作。
这样BVH的逻辑就编写完了。要注意的是这里我闹了个乌龙,bvh这里使用的是hittable **world的形式,即一个包含了很多hittable指针的数组;然而前面我们设计的时候使用的是vector<shared_ptr<hittable>>,完全对不上,所以我把后者也改成了纯指针的形式。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #ifndef HITTABLE_LIST_H #define HITTABLE_LIST_H #include"hittable.h" #include<memory> #include<vector> using std::shared_ptr; using std::make_shared; using std::vector; class hittable_list :public hittable { public: hittable** objects = new hittable*[1000]; int count = 0; public: hittable_list(){ } hittable_list(hittable* object) { add(object); } void add(hittable* object) { objects[count++]=object; } aabb getbox() const override{ return aabb(vec3(9999,9999,9999),vec3(9999,9999,9999)); } virtual bool hit(const ray& r, double tmin, double tmax, hit_record& rec) const override; }; #endif // !HITTABLE_LIST_H |
回到renderroute.cpp的loop函数这里,我们需要声明一个bvh_node的根节点,并且把hittable_list中的hittable列表全部导入。只需要写一句:bvh_node head = bvh_node(world.objects,world.count); 即可。那么在调用ray_color的时候,我们就要把ray_color(r, world, max_depth);改成ray_color(r, head, max_depth);即可。
此时进行渲染,可以清楚的看到:渲染到复杂模型的时候速度没什么太明显的变化,但是在渲染天空和地面的时候会突然加速,因为当光线射向天空和地面时,只用遍历很少的几层的bvh就能得到结果。这样渲染效率也就有了显著的提升。
接下来我们来做一点性能测试。一共测试四种情况:无BVH-无openmp;无BVH-有openmp;有BVH-非随机轴-有openmp;有BVH-随机轴-有openmp。测试的模型如下,一共400个顶点,584个面,上了一张木材的纹理。

测试结果为:无BVH-无openmp耗时2807秒;无BVH-有openmp耗时562秒;有BVH-非随机轴-有openmp耗时25秒;有BVH-随机轴-有openmp耗时15秒。可以看出,BVH在效率上的提升作用是非常显著的。而且使用随机轴排序,可以覆盖三个维度的分叉,比非随机轴排序效果更好。
重要性采样
关于重要性采样的原理和知识在我后来写的蒙特卡洛积分与重要性采样 – PULUO这篇blog中有详细解读,这里我们就不多赘述了。
一、cosine重要性采样
对于外场景而言,当我们把采样数设置为8时,其渲染结果是这样的:
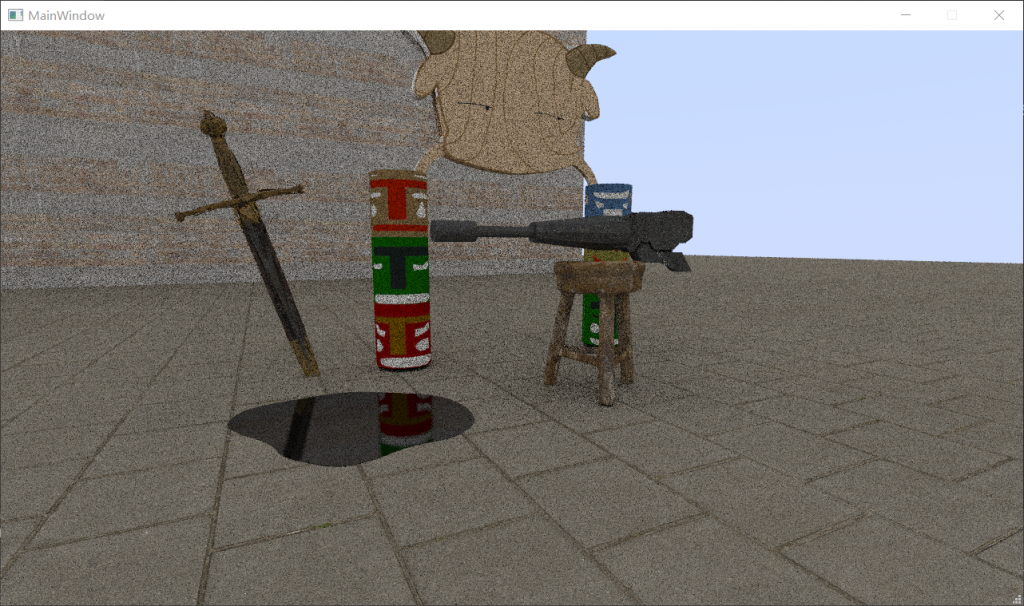
这就是使用均匀采样拟合蒙特卡洛积分的后果,噪点非常严重。这里我们可以使用cosine的重要性采样来尝试降噪:
[ccM_c]
vec3 toNormalHemisphere(vec3 v, vec3 N)const {
vec3 helper = vec3(1, 0, 0);
if(fabs(N.x())>0.999) helper = vec3(0, 1, 0);
vec3 tangent = cross(N, helper).normalize();
vec3 bitangent = cross(N, tangent).normalize();
return v.x() * tangent + v.z() * bitangent + v.y() * N;
}
vec3 SampleCosineHemisphere(float xi_1, float xi_2, vec3 N)const {
float r = sqrt(xi_1);
float theta = xi_2 * 2.0 * pi;
float x = r * cos(theta);
float z = r * sin(theta);
float y = sqrt(1.0 – xi_1);
vec3 L = toNormalHemisphere(vec3(x, y, z), N);
return L;
}
…
virtual bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered) const override {
float U1=random_double(0,1),U2=random_double(0,1);
vec3 L=SampleCosineHemisphere(U1, U2, rec.normal);
double pdf=dot(rec.normal,L.normalize())/pi;
if(pdf<0.001f)pdf=0.001f;
scattered = ray(rec.p, L);
attenuation = tex->getCol(rec.u*scaleX,rec.v*scaleY)/pdf/5;
return true;
}
[\ccM_c]
这里我们首先生成两个均匀随机数U1和U2,然后根据博客记载的算法来进行反射向量的采样,并投影到对应的半球空间;最后得到的结果除以pdf,便得到了基于cosine的重要性采样。优化结果如下:
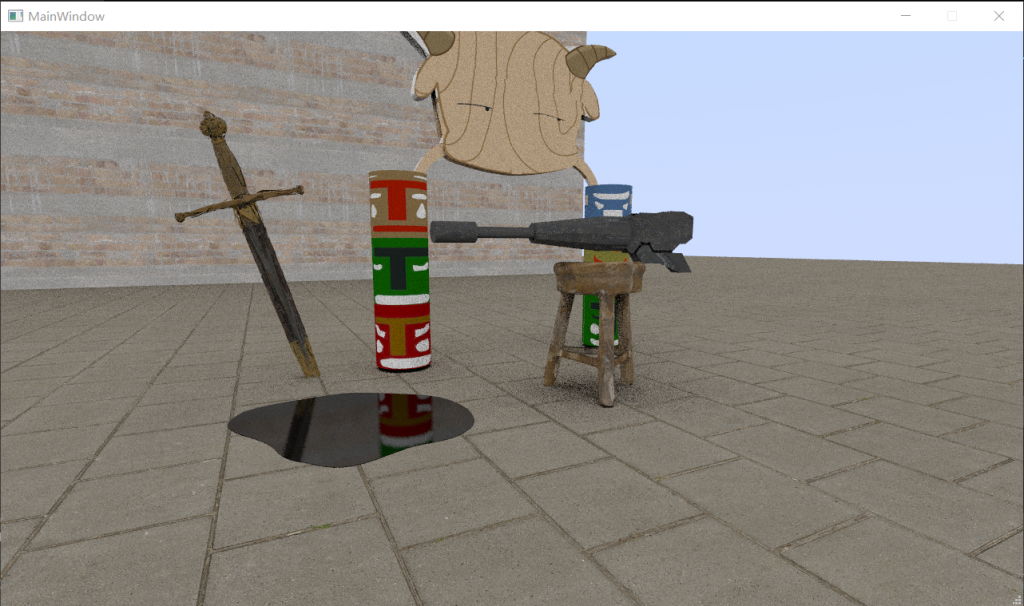
二、光源重要性采样
对于外场景而言,光源无限大,所以不愁反射光线追踪不到光源。但是在狭小的空间中,光源变成了一个很难追踪的对象,那么即使加了cosine的重要性采样,并将采样数拉到256,仍然会有非常大的噪点:
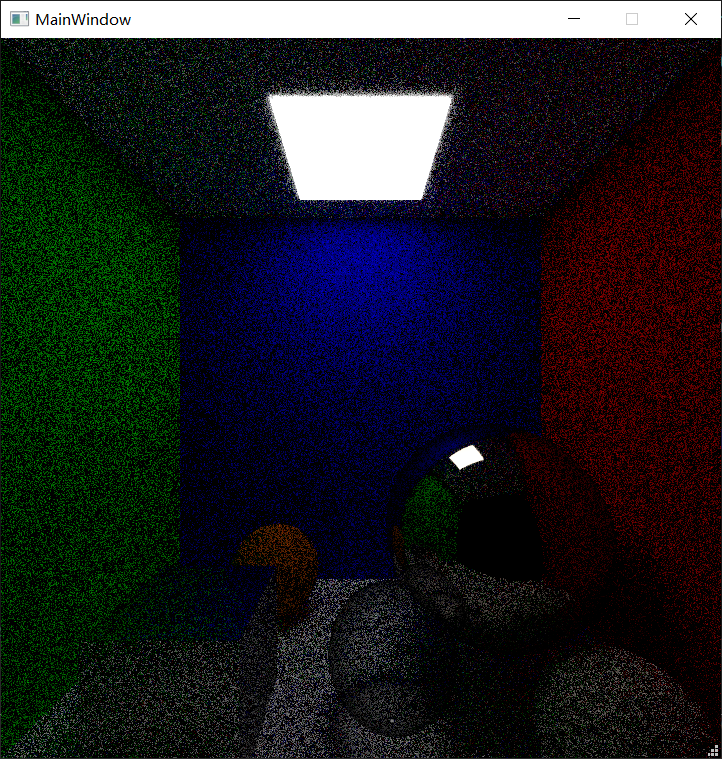
这特么啥啊,这时候就要请出我们的光源重要性采样了。之前的博客里我们使用的是这样的逻辑:将直接光照和间接光照分开,分别计算贡献和pdf:

首先我们想看看纯直接光采样的效果(将间接光先删去),代码如下:
if (world.hit(r, 0.01, infinity, rec)) {
ray scattered;
color attenuation;
if (rec.mat_ptr->scatter(r, rec, attenuation, scattered))
{
if(rec.mat_ptr->isLight == true)
return attenuation * vec3(3,3,3);
float random_goal_y = random_double(17,23);
float random_goal_z = random_double(-18,-12);
vec3 to_light = (vec3(0,random_goal_y,random_goal_z)-rec.p).normalize();
double distance = (vec3(0,random_goal_y,random_goal_z)-rec.p).length();
double pdf = 1.0f / (3 * 3);
result += vec3(8,8,8) * attenuation * dot(rec.normal,to_light) * dot(-to_light,vec3(0,-1,0)) / (distance * distance) / pdf;
return result;
}
...
这段代码中我们只考虑了直接光采样的部分,没有让他进行第二次弹射。当采样数设置为4时,结果如下:

可以看到采样数仅为4,就已经有了很平滑的柔和光照效果了!此时我们再加入我们的间接光:
if (world.hit(r, 0.01, infinity, rec)) {
ray scattered;
color attenuation;
if (rec.mat_ptr->scatter(r, rec, attenuation, scattered))
{
if(rec.mat_ptr->isLight == true){
return vec3(3,3,3);
}
float random_goal_y = random_double(17,23);
float random_goal_z = random_double(-18,-12);
vec3 to_light = (vec3(0,random_goal_y,random_goal_z)-rec.p).normalize();
double distance = (vec3(0,random_goal_y,random_goal_z)-rec.p).length();
double pdf = 1.0f / (3 * 3);
if(rec.mat_ptr->isMetal == false)
result += vec3(20,20,20) * attenuation * dot(rec.normal,to_light) * dot(-to_light,vec3(0,-1,0)) / (distance * distance) / pdf;
return result + attenuation * ray_color(scattered, world, depth - 1) * dot(scattered.direction().normalize(), rec.normal);
}
...
这里需要注意一点,那就是金属材质的物体不适用于直接光采样,因为它的反射反向是固定的,如果反射不指向光源,那么就不应该受到直接光贡献。最终采样数为4的结果如下:
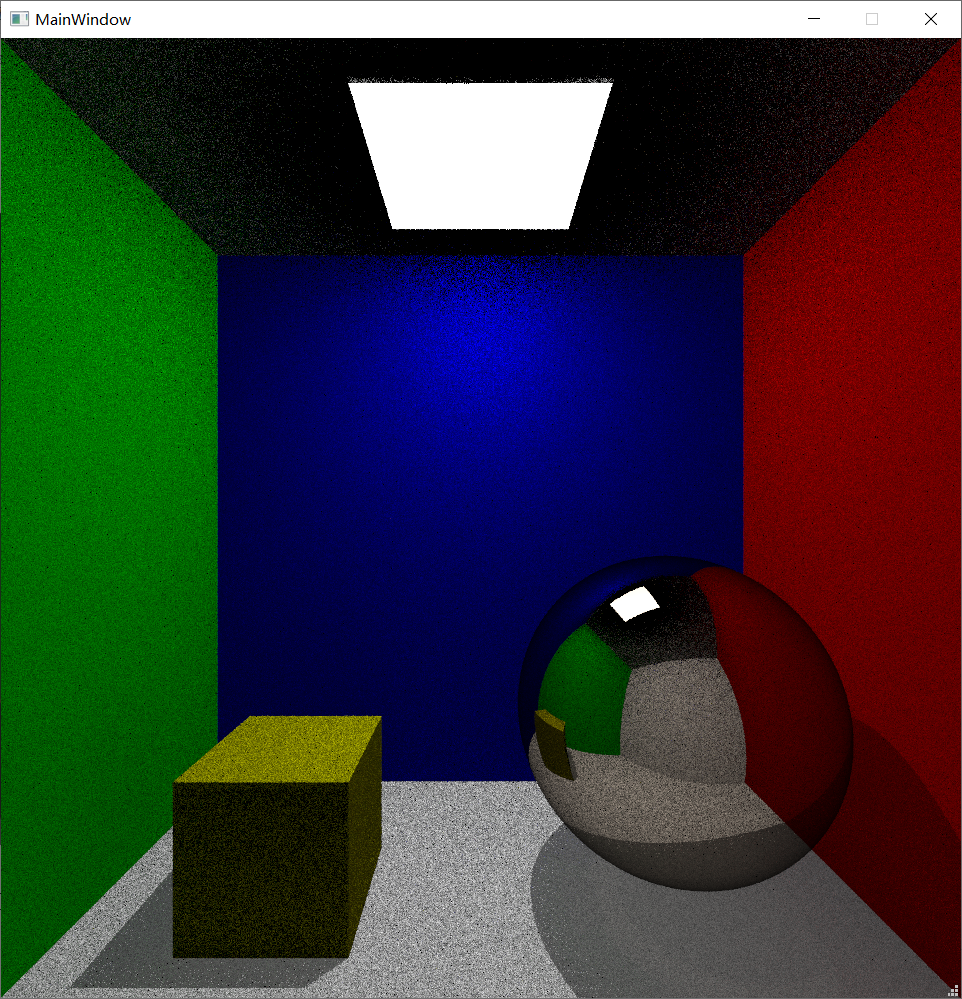
可以看到,现在使用较低的采样数也可以获得噪点不那么严重的结果了。我们直接给一个2048的采样数跑一下午看看结果:

至此,光线追踪渲染器正式收工。




2 Comments
admin
7th 9 月 2022 - 下午11:17博主,交换友情链接吗?
晨汐网
6th 12 月 2022 - 下午10:08博主你好,你的网站做得真好,可以跟你换个友链吗?