Deprecated: Function create_function() is deprecated in /www/wwwroot/puluo.top/wp-content/plugins/codecolorer/lib/geshi.php on line 4698

<script>

引言

　　前几篇博客实现了一个基于C++的光栅化软渲染器，可以看到虽然帧率还可以，但是画面效果有点不堪入目。这是因为光栅化算法的实现思路决定了，想直接模拟真实的环境效果是很困难的。那么今天我们尝试一下火遍一时的光线追踪算法，仍旧是基于Qt平台，最后对比一下光栅化和光线追踪的效果。

　　我参考的书是《Ray Tracing in One Weekend》，上面有非常丰富的解读，本篇的代码基本也是按照书上来编写的，因此本篇文章中就不详解了，只是简单放一下代码（表示我做过了）如果有非常难解的问题可以直接阅读原著。


多线程配置

　　其他大佬的渲染器都是后台导出一个ppm格式的图片，然后在用ppm图片查看器来查看结果。我这里为了感受光线追踪逐像素计算的过程，特意开了一张Qt画布来逐帧更新各个像素，这样一是不用导出奇怪的ppm格式，二是可以直接得到计算的总进度，并且在计算的同时可以观察已经计算完的像素的结果。

　　那么我们就需要用到多线程，将像素计算和画布刷新分到两个线程去完成。配置方式和软光栅渲染器的方法相同，依旧是在mainwindow的cpp中编写如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
MainWindow::MainWindow(QWidget *parent)
    : QMainWindow(parent)
    , ui(new Ui::MainWindow)
{
    int myWidth=1280,myHeight=720;
    ui-&gt;setupUi(this);
    this-&gt;resize(myWidth,myHeight);
    setFixedSize(myWidth,myHeight);
    loop=new RenderRoute(width(),height(),nullptr);
    loopThread=new QThread(this);
    loop-&gt;moveToThread(loopThread);
    connect(loopThread,&amp;QThread::finished,loop, &amp;RenderRoute::deleteLater);
    connect(loopThread,&amp;QThread::started,loop,&amp;RenderRoute::loop);
    connect(loop,&amp;RenderRoute::frameOut,this,&amp;MainWindow::receiveFrame);
    loopThread-&gt;start();
}

MainWindow::~MainWindow()
{
    delete ui;
    loopThread-&gt;quit();
    loopThread-&gt;wait();
    if(canvas)delete canvas;
    if(loopThread)delete loopThread;
    loop=nullptr;
    canvas=nullptr;
    loopThread=nullptr;
}

void MainWindow::receiveFrame(unsigned char *data)
{
    //if(canvas != nullptr) delete canvas;
    canvas = new QImage(data, width(), height(), QImage::Format_RGBA8888);
    update();
}

void MainWindow::paintEvent(QPaintEvent *event)
{
    if(canvas)
    {
        QPainter painter(this);
        painter.drawImage(0,0,*canvas);
    }
    QWidget::paintEvent(event);
}

　　阅读过软光栅blog的童鞋应该比较熟悉了，构造函数是在定义画布尺寸、将RenderRoute绑定到新的线程，然后将RenderRoute中的frameOut发射器和这里的receiveFrame接收器绑定；

　　receiveFrame接收器接收到像素后，就可以更新画布了，接下来调用update函数，它会自动调用刷新画布的函数paintEvent，这里我们override一下这个paintEvent函数即可。


编写基础库

　　在一切工作开始前，我们需要编写一些全局可用的变量或方法，这里我们命名为rtweekend.h，其中包含了各种常量、随机数生成方法、clamp方法等，基本上后续的所有类都需要调用它：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#ifndef RTWEEKEND_H
#define RTWEEKEND_H

#include<cmath>
#include<cstdlib>
#include<limits>
#include<memory>

using std::shared_ptr;
using std::make_shared;
using std::sqrt;

//常量
const double infinity = std::numeric_limits<double>::infinity();
const double pi = 3.1415926535897932385;

//函数
inline double degrees_to_radians(double degrees) {
    return degrees * pi / 180.0;
}
inline double random_double() {
    //[0,1)
    return rand() / (RAND_MAX + 1.0);
}

inline double random_double(double min, double max) {
    //[min,max)
    return min + (max - min) * random_double();
}

inline double clamp(double x, double min, double max) {
    if (x < min) return min;
    if (x > max) return max;
    return x;
}

#endif // !RTWEEKEND_H

　　接下来我们还是先编写数学库。和软光栅不同，这里我们只需要用到三维向量，因为第四维的w在光追里没有被用到；同时矩阵也不再必要了，因为我们没有用到复杂的空间变换。这部分也相当简单，不再赘述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#ifndef VEC3_H
#define VEC3_H

#include<cmath>
#include<iostream>
#include"rtweekend.h"
using std::sqrt;

class vec3 {
public:
    double e[3];
public:
    //构造函数
    vec3() :e{ 0,0,0 } { }
    vec3(double e0, double e1, double e2) :e{ e0, e1, e2 } { }
    //坐标
    double x() const { return e[0]; }
    double y() const { return e[1]; }
    double z() const { return e[2]; }
    //运算符
    vec3 operator-() const { return vec3(-e[0], -e[1], -e[2]); }
    double operator[](int i) const { return e[i]; }
    double&amp; operator[](int i) { return e[i]; }
    vec3&amp; operator+=(const vec3&amp; v) {
        e[0] += v.e[0];
        e[1] += v.e[1];
        e[2] += v.e[2];
        return *this;
    }
    vec3&amp; operator*=(const double t) {
        e[0] *= t;
        e[1] *= t;
        e[2] *= t;
        return *this;
    }
    vec3&amp; operator/=(const double t) {
        return *this *= 1 / t;
    }
    //长度相关
    double length() const {
        return sqrt(length_squared());
    }
    double length_squared() const {
        return e[0] * e[0] + e[1] * e[1] + e[2] * e[2];
    }
    static vec3 random() {
        return vec3(random_double(), random_double(), random_double());
    }
    static vec3 random(double min, double max) {
        return vec3(random_double(min, max), random_double(min, max), random_double(min, max));
    }
};

using point3 = vec3;    //3D point
using color = vec3;     //RGB color

// vec3 Utility Functions
inline std::ostream&amp; operator&lt;&lt;(std::ostream&amp; out, const vec3&amp; v) {
    return out &lt;&lt; v.e[0] &lt;&lt; ' ' &lt;&lt; v.e[1] &lt;&lt; ' ' &lt;&lt; v.e[2];
}
inline vec3 operator+(const vec3&amp; u, const vec3&amp; v) {
    return vec3(u.e[0] + v.e[0], u.e[1] + v.e[1], u.e[2] + v.e[2]);
}
inline vec3 operator-(const vec3&amp; u, const vec3&amp; v) {
    return vec3(u.e[0] - v.e[0], u.e[1] - v.e[1], u.e[2] - v.e[2]);
}
inline vec3 operator*(const vec3&amp; u, const vec3&amp; v) {
    return vec3(u.e[0] * v.e[0], u.e[1] * v.e[1], u.e[2] * v.e[2]);
}
inline vec3 operator*(double t, const vec3&amp; v) {
    return vec3(t * v.e[0], t * v.e[1], t * v.e[2]);
}
inline vec3 operator*(const vec3&amp; v, double t) {
    return t * v;
}
inline vec3 operator/(const vec3&amp; v, double t) {
    return (1 / t) * v;
}
//数量积
inline double dot(const vec3&amp; u, const vec3&amp; v) {
    return u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2];
}
//叉乘
inline vec3 cross(const vec3&amp; u, const vec3&amp; v) {
    return vec3(u.e[1] * v.e[2] - u.e[2] * v.e[1],
        u.e[2] * v.e[0] - u.e[0] * v.e[2],
        u.e[0] * v.e[1] - u.e[1] * v.e[0]);
}
inline vec3 unit_vector(const vec3&amp; v) {
    return v / v.length();
}
//普通函数
static vec3 random_unit_vector() {
    auto a = random_double(0, 2 * pi);
    auto z = random_double(-1, 1);
    auto r = sqrt(1 - z * z);
    return vec3(r * cos(a), r * sin(a), z);
}
static vec3 random_in_unit_disk() {
    while (true) {
        auto p = vec3(random_double(-1, 1), random_double(-1, 1), 0);
        if (p.length_squared() &gt;= 1)
            continue;
        return p;
    }
}

#endif // VEC3_H

　　这里要注意的是，我们把vec3又typedef了一份color，一份point3。vec3、color、point3分别表示向量、rgb颜色和点的坐标，这样更容易理解指定变量的含义，不易混淆。


射线构建

　　射线是光线追踪最重要、最基础的东西。光线追踪的本质意义就是，从眼睛（即相机）射出射线，然后让射线在场景中进行碰撞、折射或反射，来获取颜色信息。因此射线是一切行为的基础，我们接下来便开始定义射线。

　　射线由哪些数学量决定呢？很容易知道由一个原点（origin）和一个向量（direction）决定。原点就是射线发射的起点，向量包含了射线的方向以及长度。

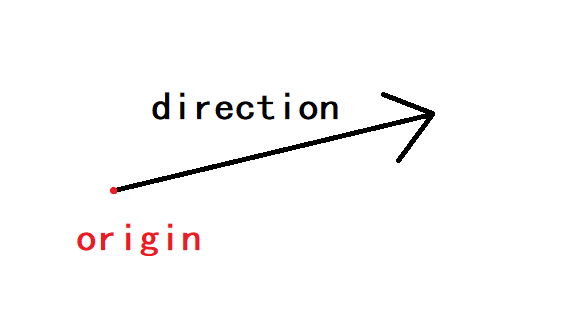
　　我们知道射线从原点射出，随着时间推移会越射越远，因此射线射到的点的坐标是关于t的函数。因此我们的Ray类就可以这样编写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#ifndef RAY_H
#define RAY_H

#include"vec3.h"

class ray {
public:
    point3 orig;
    vec3 dir;
public:
    ray(){}
    ray(const point3&amp; origin, const vec3&amp; direction) :orig(origin),dir(direction){ }

    point3 origin() const { return orig; }
    vec3 direction() const { return dir; }

    point3 at(double t) const {
        return orig + t * dir;
    }
};

#endif // RAY_H


相机

　　光追的相机和光栅化的相机有一点区别，这里我们的相机只有一个终极任务：在获得屏幕上像素的屏幕坐标后，向场景发射出相应的射线。当然要做到这件事，我们首先要对相机进行一些基础配置。

　　这里引用一张csdn上某大佬的图：

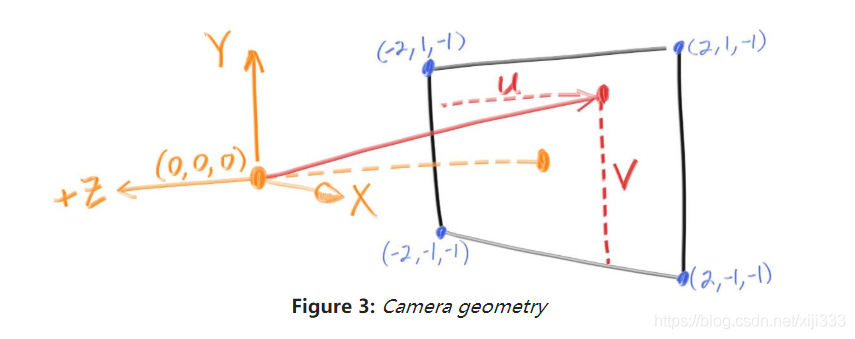
　　这里我们可以看到一些事情：首先相机和成像屏幕不在一起，相机在成像屏幕的后方（z相机>z屏幕）；相机拥有三个轴u、v、w，当相机没有旋转的时候，其三个轴就与图中的x、y、z轴重合，但是绝大部分情况下需要先给出相机位置、看向点的位置、相机上方向量这三个参量，才能决定u、v、w的方向。

　　除此之外有一个拓展内容，就是光圈。也就是说，最后射入相机的光线并非汇聚为一个点，而是聚在一个圆形范围内。这也就意味着：穿过屏幕上同一个像素的光线可能来自不同的方向（仔细思考这一点），它们携带的是不同的颜色信息，最后共同作用到同一个像素上，这就呈现出了景深模糊的效果。

　　最后就是射出射线的方法，也就是说屏幕上某个像素把自己的横纵位置给相机，相机能够计算出从该像素射出的射线结构（origin和direction）。要注意的是相机有光圈，因此射线的起点是一个圆内的随机值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#ifndef CAMERA_H
#define CAMERA_H

#include"rtweekend.h"
#include"vec3.h"
#include"ray.h"

class camera {
private:
    point3 origin;
    point3 lower_left_corner;
    vec3 horizontal;
    vec3 vertical;
    vec3 u, v, w;
    double lens_radius;
public:
    camera(point3 lookfrom, point3 lookat, vec3 vup, double vfov, double aspect_ratio,double aperture,double focus_dist) {
        auto theta = degrees_to_radians(vfov);
        auto h = tan(theta / 2);
        auto viewport_height = 2.0 * h;
        auto viewport_width = aspect_ratio * viewport_height;

        w = unit_vector(lookfrom - lookat);
        u = unit_vector(cross(vup, w));
        v = cross(w, u);

        origin = lookfrom;
        horizontal = focus_dist * viewport_width * u;
        vertical = focus_dist * viewport_height * v;
        lower_left_corner = origin - horizontal / 2 - vertical / 2 - focus_dist * w;
        lens_radius = aperture / 2;
    }

    ray get_ray(double s, double t) const {
        vec3 rd = lens_radius * random_in_unit_disk();
        vec3 offset = u * rd.x() + v * rd.y();
        return ray(origin + offset, lower_left_corner + s * horizontal + t * vertical - origin - offset);
    }
};
#endif // !CAMERA_H


可碰撞结构

　　射线有一项重要的任务是与物体进行求交，即计算射线和物体碰撞。可以碰撞的物体有很多种，例如球体，三角形，其它多边形等等，因此我们可以抽象成一个抽象类hittable，它的接口则是求交（碰撞）函数hit。

　　在介绍hit函数之前，需要再额外引入一个内容，就是hit_record结构体，它的作用是记录碰撞信息，包括交点、交点处法向量、对象材质、射线从出发到碰撞的距离、面朝向等等。当一根射线在场景中漫游时，需要时刻携带并维护hit_record，为自己记录上次或本次的碰撞信息。

　　那么接下来介绍下hit函数，它就是接收射线信息，根据射线的最短运行时间限制和最长运行时间限制来判断是否为有效求交，然后再在函数中编写求交逻辑。如果求交成功，则将碰撞信息写入hit_record中。

　　可以这么理解这件事：hittable本质就是场景中的物体，扮演服务员的角色。射线是顾客，他把自己的信息hit_record递给服务员，服务员后台计算射线的信息，最后把碰撞结果写入信息中，让顾客离开。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#ifndef HITTABLE_H
#define HITTABLE_H

#include"ray.h"

class material;

struct hit_record {
    point3 p;   //交点
    vec3 normal;    //法向量
    shared_ptr<material> mat_ptr;
    double t;   //距离
    bool front_face;

    inline void set_face_normal(const ray& r, const vec3& outward_normal) {
        front_face = dot(r.direction(), outward_normal) < 0;
        normal = front_face ? outward_normal : -outward_normal;
    }
};

class hittable {
public:
    virtual bool hit(const ray& r, double t_min, double t_max, hit_record& rec) const = 0;
};
#endif // ! HITTABLE_H

　　接下来我们再考虑一件事：场景中的可碰撞体非常多，需要用一种数据结构将它们包装起来。这样射线在求交的时候，可以直接提取数据结构中的内容，从而快速遍历所有可碰撞体。因此可以定义一个hitable_list类，用来装所有的可碰撞体。

　　在实现上，我们可以让list继承hittable，那么我们就需要override hit函数。list的hit函数本质上就是调用表中所有可碰撞体的hit，同时计算哪个物体距离射线起点最近（射线优先击中最近的物体），那么该物体就是射线与场景所有物体求交的结果对象。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#ifndef HITTABLE_LIST_H
#define HITTABLE_LIST_H

#include"hittable.h"
#include<memory>
#include<vector>

using std::shared_ptr;
using std::make_shared;
using std::vector;

class hittable_list :public hittable {
public:
    vector<shared_ptr<hittable>> objects;
public:
    hittable_list(){ }
    hittable_list(shared_ptr<hittable> object) { add(object); }

    void clear() { objects.clear(); }
    void add(shared_ptr<hittable> object) { objects.push_back(object); }

    virtual bool hit(const ray& r, double tmin, double tmax, hit_record& rec) const override;
};

#endif // !HITTABLE_LIST_H
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include "hittable_list.h"

bool hittable_list::hit(const ray&amp; r, double t_min, double t_max, hit_record&amp; rec) const {
    hit_record temp_rec;
    bool hit_anything = false;
    double closest_so_far = t_max;
    for (const auto&amp; object : objects) {
        if (object-&gt;hit(r, t_min, closest_so_far, temp_rec)) {
            hit_anything = true;
            closest_so_far = temp_rec.t;
            rec = temp_rec;
        }
    }
    return hit_anything;
}

　　说了这么多，具体几何物体的hit函数还没介绍怎么写，接下来介绍下这部分内容。


经典几何体

　　首先介绍下最简单的可碰撞体：球体。易知球体的参数有：球心坐标、球半径、球体材质（材质需要定义为指针形式，原因放后面说）

　　类的核心在于如何override hit函数。我们现在需要做的事情就是：已知球体坐标半径，已知射线的向量表示，如何计算是否能碰撞，以及碰撞点的坐标。这里白嫖大师上线，上一张白嫖的图：

　　就不从头带着推导了，有心情可以按上图推一边，没心情直接看结论就行。最后本质上是一个二元一次方程，通过求判别式、使用求根公式来判断是否有交点以及交点位置在哪。一旦碰撞成功，函数就需要维护hit_record信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#ifndef SPHERE_H
#define SPHERE_H

#include"hittable.h"
#include"vec3.h"

class sphere :public hittable {
public:
    point3 center;
    double radius;
    shared_ptr<material> mat_ptr;
public:
    sphere() { }
    sphere(point3 cen, double r, shared_ptr<material> mat) :center(cen), radius(r),mat_ptr(mat) { }

    virtual bool hit(const ray& r, double t_min, double t_max, hit_record& rec) const override;
};

#endif // ! SPHERE_H
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include "sphere.h"

bool sphere::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    vec3 oc = r.origin() - center;
    double a = r.direction().length_squared();
    double half_b = dot(r.direction(), oc);
    double c = oc.length_squared() - radius * radius;
    double discriminant = half_b * half_b - a * c;
    if (discriminant > 0) {
        double root = sqrt(discriminant);
        double t = (-half_b - root) / a;
        if (t > t_min&& t < t_max) {
            rec.t = t;
            rec.p = r.at(t);
            vec3 outward_normal = (rec.p - center) / radius;
            rec.set_face_normal(r, outward_normal);
            rec.mat_ptr = mat_ptr;
            return true;
        }
        t = (-half_b + root) / a;
        if (t > t_min&& t < t_max) {
            rec.t = t;
            rec.p = r.at(t);
            vec3 outward_normal = (rec.p - center) / radius;
            rec.set_face_normal(r, outward_normal);
            rec.mat_ptr = mat_ptr;
            return true;
        }
    }
    return false;
}

　　然后说下三角形。三角形一共分为两步：首先根据三角形三个点和射线的关系，计算出射线与三角形所在平面的交点；之后计算交点是否在三角形面内。首先看一下如何求出与平面的交点：

$$P_t=O+tD$$

$$n·(P-P_0)=0$$

$$n·(O+tD-P_0)=0$$

　　上述形式是满足分配律的，因为：

$$(a,b,c)·[(i,j,k)+(x,y,z)]=a(i+x)+b(j+y)+c(k+z)=(a,b,c)·(i,j,k)+(a,b,c)·(x,y,z)$$

　　所以可以拆开：

$$n·O+tn·D-n·P_0=0$$

$$t=\frac{n·P_0-n·O}{n·D}$$

　　这样我们就得到了t的值，那么交点坐标就是O+n·D了。接下来我们还需要判断是否在三角形内，这个算是比较经典的算法问题了，我们可以用最传统的叉乘法来解决：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#ifndef TRIANGLE_H
#define TRIANGLE_H


#include"hittable.h"
#include"vec3.h"

class triangle :public hittable {
public:
    point3 pt[3];
    vec3 normal;
    shared_ptr<material> mat_ptr;
public:
    triangle() { }
    triangle(point3 a, point3 b, point3 c, shared_ptr<material> mat): pt{a,b,c},mat_ptr(mat)
    {
        vec3 v1=(pt[0]-pt[1]);
        vec3 v2=(pt[1]-pt[2]);
        normal=cross(v1,v2);
        normal/=normal.length();
    }
    triangle(point3 a, point3 b, point3 c, vec3 n, shared_ptr<material> mat): pt{a,b,c},mat_ptr(mat)
    {
        normal=n/n.length();
    }
    bool SameSide(vec3 A, vec3 B, vec3 C, vec3 P)const;
    virtual bool hit(const ray&amp; r, double t_min, double t_max, hit_record&amp; rec) const override;
};

class cube
{
public:
    shared_ptr<triangle> tg[120];
    int faceCnt=12;
    shared_ptr<material> mat_ptr;
public:
    cube(){}
    cube(point3 pos,double size,shared_ptr<material> mat):mat_ptr(mat)
    {
        double half=size/2;
        /*前面*/
        tg[0]=make_shared<triangle>(pos+vec3(-half,half,half),pos+vec3(half,half,half),
                       pos+vec3(-half,-half,half),vec3(0,0,1),mat_ptr);
        tg[1]=make_shared<triangle>(pos+vec3(half,-half,half),pos+vec3(half,half,half),
                       pos+vec3(-half,-half,half),vec3(0,0,1),mat_ptr);
        /*上面*/
        tg[2]=make_shared<triangle>(pos+vec3(-half,half,-half),pos+vec3(half,half,-half),
                       pos+vec3(-half,half,half),vec3(0,1,0),mat_ptr);
        tg[3]=make_shared<triangle>(pos+vec3(half,half,half),pos+vec3(half,half,-half),
                       pos+vec3(-half,half,half),vec3(0,1,0),mat_ptr);
        /*右面*/
        tg[4]=make_shared<triangle>(pos+vec3(half,half,half),pos+vec3(half,half,-half),
                       pos+vec3(half,-half,half),vec3(1,0,0),mat_ptr);
        tg[5]=make_shared<triangle>(pos+vec3(half,-half,-half),pos+vec3(half,half,-half),
                       pos+vec3(half,-half,half),vec3(1,0,0),mat_ptr);
        /*后面*/
        tg[6]=make_shared<triangle>(pos+vec3(-half,half,-half),pos+vec3(half,half,-half),
                       pos+vec3(-half,-half,-half),vec3(0,0,-1),mat_ptr);
        tg[7]=make_shared<triangle>(pos+vec3(half,-half,-half),pos+vec3(half,half,-half),
                       pos+vec3(-half,-half,-half),vec3(0,0,-1),mat_ptr);
        /*下面*/
        tg[8]=make_shared<triangle>(pos+vec3(-half,-half,-half),pos+vec3(half,-half,-half),
                       pos+vec3(-half,-half,half),vec3(0,-1,0),mat_ptr);
        tg[9]=make_shared<triangle>(pos+vec3(half,-half,half),pos+vec3(half,-half,-half),
                       pos+vec3(-half,-half,half),vec3(0,-1,0),mat_ptr);
        /*左面*/
        tg[10]=make_shared<triangle>(pos+vec3(-half,half,half),pos+vec3(-half,half,-half),
                       pos+vec3(-half,-half,half),vec3(-1,0,0),mat_ptr);
        tg[11]=make_shared<triangle>(pos+vec3(-half,-half,-half),pos+vec3(-half,half,-half),
                       pos+vec3(-half,-half,half),vec3(-1,0,0),mat_ptr);
    }
};

#endif // TRIANGLE_H

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include "triangle.h"
bool triangle::SameSide(vec3 A, vec3 B, vec3 C, vec3 P)const
{
    vec3 AB = B - A ;
    vec3 AC = C - A ;
    vec3 AP = P - A ;

    vec3 v1 = cross(AB,AC) ;
    vec3 v2 = cross(AB,AP) ;

    return dot(v1,v2) &gt;= 0 ;
}

bool triangle::hit(const ray&amp; r, double t_min, double t_max, hit_record&amp; rec) const {
    /*n.(p0- porig)/ n.vDir*/
    //if(dot(normal,r.direction())==0)return false;
    double t=dot(normal,pt[0]-r.origin())/dot(normal,r.direction());

    if (t &gt; t_min&amp;&amp; t &lt; t_max)
    {
        point3 P=r.at(t);
        if(SameSide(pt[0],pt[1],pt[2],P) &amp;&amp; SameSide(pt[1],pt[2],pt[0],P)
                &amp;&amp;SameSide(pt[2],pt[0],pt[1],P))
        {
            rec.t=t;
            rec.p=r.at(t);
            rec.set_face_normal(r,normal);
            rec.mat_ptr=mat_ptr;
            return true;
        }
    }
    return false;
}

　　如此，我们便完成了最基础的两种可碰撞体类的编写了。


材质

　　如果所有物体全部是一片土灰，那么场景的感染力将直线下滑。如何体现出绚丽多姿的物体表面呢，那自然要请到材质出马了。材质是图形界一个避不开的话题，有别于光栅化管线渲染的材质，这里的材质将会对物体表面的物理性质进行描述。什么叫物理性质呢？在这里说的其实就是：光线打到表面上之后会发生什么。所以我们可以定义一个抽象类material，以及唯一的接口scattering（散射）。

　　散射接口需要传入的参数有：入射光线、碰撞记录、颜色衰减、出射光线。颜色衰减指的是一部分颜色被材质吸收以后，剩余rgb与吸收前的占比（例如(1,0,0)表示绿色和蓝色都被吸收了，那么光线从材质上弹出的就只有红光了）。出射光线默认是不知道的，传入的出射光线是个引用，在函数中完成赋值。

1
2
3
4
5
6
7
8
9
10
11
#ifndef  MATERIAL_H
#define  MATERIAL_H

#include"rtweekend.h"
#include"hittable.h"
#include"texture.h"

class material {
public:
    virtual bool scatter(const ray&amp; r_in, const hit_record&amp; rec, color&amp; attenuation, ray&amp; scattered) const = 0;
};

　　接下来介绍4种基础材质类型，分别是：均匀漫反射、镜面反射、透射、棋盘纹理材质。这四种材质都比较基础，就不详细介绍它们的来源了。均匀漫反射、镜面反射前面已经都介绍过了，透射其实也和之前介绍的类似，只是将菲涅尔定律的严谨定义换了个好计算的公式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
class lambertian :public material {
public:
    color albedo;
public:
    lambertian(const color&amp; a) :albedo(a) { }
    virtual bool scatter(const ray&amp; r_in, const hit_record&amp; rec, color&amp; attenuation, ray&amp; scattered) const override {
            vec3 scatter_direction = rec.normal + random_unit_vector();
            scattered = ray(rec.p, scatter_direction);
            attenuation = albedo;
            return true;
        }
    //virtual bool scatter(const ray&amp; r_in, const hit_record&amp; rec, color&amp; attenuation, ray&amp; scattered) const override;
};

class metal :public material {
public:
    color albedo;
    double fuzz;
public:
    metal(const color&amp; a, double f) :albedo(a), fuzz(f &lt; 1 ? f : 1) { }
    vec3 reflect(const vec3&amp; v, const vec3&amp; n) const{
        return v - 2 * dot(v, n) * n;
    }
    virtual bool scatter(const ray&amp; r_in, const hit_record&amp; rec, color&amp; attenuation, ray&amp; scattered) const override {
            vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
            scattered = ray(rec.p, reflected + fuzz * random_unit_vector());
            attenuation = albedo;
            return (dot(scattered.direction(), rec.normal) &gt; 0);
        }
    //virtual bool scatter(const ray&amp; r_in, const hit_record&amp; rec, color&amp; attenuation, ray&amp; scattered) const override;
};

class dielectric :public material {
public:
    dielectric(double ri) :ref_idx(ri) { }
    vec3 reflect(const vec3&amp; v, const vec3&amp; n) const{
        return v - 2 * dot(v, n) * n;
    }
    vec3 refract(const vec3&amp; uv, const vec3&amp; n, double etai_over_etat) const{
        auto cos_theta = dot(-uv, n);
        vec3 r_out_perp = etai_over_etat * (uv + cos_theta * n);
        vec3 r_out_parallel = -sqrt(fabs(1.0 - r_out_perp.length_squared())) * n;
        return r_out_perp + r_out_parallel;
    }
    double schlick(double cosine, double ref_idx) const{
        auto r0 = (1 - ref_idx) / (1 + ref_idx);
        r0 *= r0;
        return r0 + (1 - r0) * pow((1 - cosine), 5);
    }

    virtual bool scatter(const ray&amp; r_in, const hit_record&amp; rec, color&amp; attenuation, ray&amp; scattered) const override {
        attenuation = color(1.0, 1.0, 1.0);
        //判断交点是在外部还是内部 front_face为true时--&gt;外部
        double etai_over_etat = rec.front_face ? (1.0 / ref_idx) : ref_idx;
        vec3 unit_direction = unit_vector(r_in.direction());
        double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
        double sin_theta = sqrt(1.0 - cos_theta * cos_theta);
        if (etai_over_etat * sin_theta &gt; 1.0) { //全内反射
            vec3 reflected = reflect(unit_direction, rec.normal);
            scattered = ray(rec.p, reflected);
            return true;
        }
        double reflect_prob = schlick(cos_theta, etai_over_etat);//反射率
        if (random_double() &lt; reflect_prob) {
            vec3 reflected = reflect(unit_direction, rec.normal);
            scattered = ray(rec.p, reflected);
            return true;
        }
        vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);
        scattered = ray(rec.p, refracted);
        return true;
    }
public:
    double ref_idx;
};

　　现在就差个棋盘材质了，在此之前，得再引入一个Texture的概念。


纹理

　　纹理类其实很简单，无非就是个装rgb的数组。因此基类可以定义一个颜色数组，编写一个获取某个像素颜色的方法即可。那么接下来我们建立一个棋盘纹理chessTexture，要注意的是chessTexture和普通纹理不同，它是可无限扩展的、严谨的周期纹理，所以我们不需要手动对rgb数组赋值，而是在材质查询纹理的时候，直接根据像素坐标计算出一个颜色返还即可。棋盘纹理的像素颜色计算使用了一个正弦公式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#ifndef TEXTURE_H
#define TEXTURE_H
#include"vec3.h"

class texture
{
public:
    color col[256][256];
    texture(){}
};

class chessTexture : texture
{
public:
    color getCol(point3 p)
    {
        double tmp=sin(6 * p.x()) * sin(6 * p.y()) * sin(6 * p.z());
        if (tmp < 0)
            return color(0,0,0);
        else
            return color(1,1,1);
    }
};

#endif // TEXTURE_H

　　那么在材质类中，就可以补充棋盘材质的内容了：

1
2
3
4
5
6
7
8
9
10
11
12
13
class lambertianChess :public material {
public:
    shared_ptr<chessTexture> tex;
public:
    lambertianChess(const shared_ptr<chessTexture> a) :tex(a) { }
    virtual bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered) const override {
            vec3 scatter_direction = rec.normal + random_unit_vector();
            scattered = ray(rec.p, scatter_direction);
            attenuation = tex->getCol(rec.p);
            return true;
        }
    //virtual bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered) const override;
};


主程序

　　多线程的入口在renderRoute的Loop函数中，因此我们可以把Loop函数当做main函数来写。首先我们要定义窗口大小、相机性质，然后随机化一个场景出来。随机化我使用的是random_scene，方法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
hittable_list random_scene() {
    hittable_list world;

    //auto ground_material = make_shared<lambertian>(color(0.5, 0.5, 0.5));//地面
    auto mat = make_shared<lambertian>(color(0.4, 0.2, 0.1));
    auto ground_material = make_shared<lambertianChess>(make_shared<chessTexture>());
    world.add(make_shared<sphere>(point3(0, -1000, 0), 1000, ground_material));
    srand(time(NULL));
    for (int a = -4; a < 4; a++) {
        for (int b = -6; b < 3; b++) {
            auto choose_mat = random_double(); //随机材质
            auto choose_shape = random_double(); //随机材质
            point3 center(a + 0.9 * random_double(), 0.2, b + 0.9 * random_double()); //随机中心

            //if ((center - point3(4, 0.2, 0)).length() > 0.9) {
            if(1){
                shared_ptr<material> sphere_material;

                if (choose_mat < 0.4) {
                    // diffuse 漫反射
                    auto albedo = color::random() * color::random();
                    sphere_material = make_shared<lambertian>(albedo);
                    if(choose_shape<0.7)
                        world.add(make_shared<sphere>(center, 0.2, sphere_material));
                    else
                    {
                        auto c=cube(center,0.4,sphere_material);
                        for(int i=0;i<12;i++)
                            world.add(c.tg[i]);
                    }
                }
                else if (choose_mat < 0.6) {
                    // metal 金属
                    auto albedo = color::random(0.5, 1);
                    auto fuzz = random_double(0, 0.5);
                    sphere_material = make_shared<metal>(albedo, fuzz);
                    if(choose_shape<0.7)
                        world.add(make_shared<sphere>(center, 0.2, sphere_material));
                    else
                    {
                        auto c=cube(center,0.4,sphere_material);
                        for(int i=0;i<12;i++)
                            world.add(c.tg[i]);
                    }
                }
                else {
                    // glass 玻璃
                    sphere_material = make_shared<dielectric>(1.5);
                    if(choose_shape<0.7)
                        world.add(make_shared<sphere>(center, 0.2, sphere_material));
                    else
                    {
                        auto c=cube(center,0.4,sphere_material);
                        for(int i=0;i<12;i++)
                            world.add(c.tg[i]);
                    }
                }
            }
        }
    }

    auto material1 = make_shared<dielectric>(1.5);
    world.add(make_shared<sphere>(point3(4, 0.7, 0), 0.5, material1));

    auto material2 = make_shared<lambertian>(color(0.4, 0.2, 0.1));
    world.add(make_shared<sphere>(point3(-4, 0.7, 0), 0.7, material2));

    auto material3 = make_shared<metal>(color(0.7, 0.6, 0.5), 0.0);
    world.add(make_shared<sphere>(point3(0, 0.5, 0), 0.7, material3));

    return world;
}

　　然后我们就要遍历窗口的每一个像素，去调用相机的射出射线方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
void RenderRoute::write_color(int h, int w, color pixel_color, int samples_per_pixel) {
    auto r = pixel_color.x();
    auto g = pixel_color.y();
    auto b = pixel_color.z();
    //根据样本数对颜色取平均值
    auto scale = 1.0 / samples_per_pixel;
    r = sqrt(r * scale);
    g = sqrt(g * scale);
    b = sqrt(b * scale);
    /*col[h*800+w]=static_cast<int>(256 * clamp(r, 0.0, 0.999));
    col[h*800+w+1]=static_cast<int>(256 * clamp(g, 0.0, 0.999));
    col[h*800+w+2]=static_cast<int>(256 * clamp(b, 0.0, 0.999));*/
    col[(h*image_width+w)*4]=static_cast<int>(256 * clamp(r, 0.0, 0.999));
    col[(h*image_width+w)*4+1]=static_cast<int>(256 * clamp(g, 0.0, 0.999));
    col[(h*image_width+w)*4+2]=static_cast<int>(256 * clamp(b, 0.0, 0.999));
    col[(h*image_width+w)*4+3]=255;
}

void RenderRoute::loop() {
    const double aspect_ratio = (double)image_width / (double)image_height;
    const int samples_per_pixel = 50;
    auto world = random_scene();
    //auto world = triangle_scene();
    point3 lookfrom(0, 1.5, 5);
    point3 lookat(0, 0, -1);
    vec3 vup(0, 1, 0);
    auto dist_to_focus = (lookfrom - lookat).length();
    auto aperture = 0.005;
    camera cam(lookfrom, lookat, vup, 60, aspect_ratio, aperture, dist_to_focus);
#pragma omp parallel for
    for (int j = image_height - 1; j >= 0; --j) {
        for (int i = 0; i < image_width; ++i) {
            color pixel_color(0, 0, 0);
            for (int s = 0; s < samples_per_pixel; ++s) {
                auto u = (i + random_double()) / (image_width - 1);
                auto v = (j + random_double()) / (image_height - 1);
                ray r = cam.get_ray(u, v);
                pixel_color += ray_color(r, world, max_depth);
            }
            write_color(image_height-j,i,pixel_color, samples_per_pixel);//取平均值
            emit frameOut(col);
        }
    }
}

　　现在就缺一个最重要的内容了：ray_color方法。这个方法的作用在于，给定从视口射出的射线，返还光追结果。因此ray_color方法就是光追的核心程序。这里直接给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
color ray_color(const ray& r, const hittable& world, int depth) {
    if(depth <= 0)
        return color(0, 0, 0);
    hit_record rec;
    if (world.hit(r, 0.001, infinity, rec)) {
        ray scattered;
        color attenuation;
        if (rec.mat_ptr->scatter(r, rec, attenuation, scattered))
            return attenuation * ray_color(scattered, world, depth - 1);
        return color(0, 0, 0);
    }
    vec3 unit_direction = unit_vector(r.direction());
    double t = 0.5 * (unit_direction.y() + 1.0);
    return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}

　　其实思路还是比较清晰的。首先判断是否递归过深，然后便开始与list中的物体进行求交，得到碰撞信息，然后把碰撞信息、入射光线等信息送到对应物体的材质上进行出射光线的计算，得到出射光线后便开始下一层递归，直到打到天空为止。

　　那么总体程序就结束了，放一张光追结果：


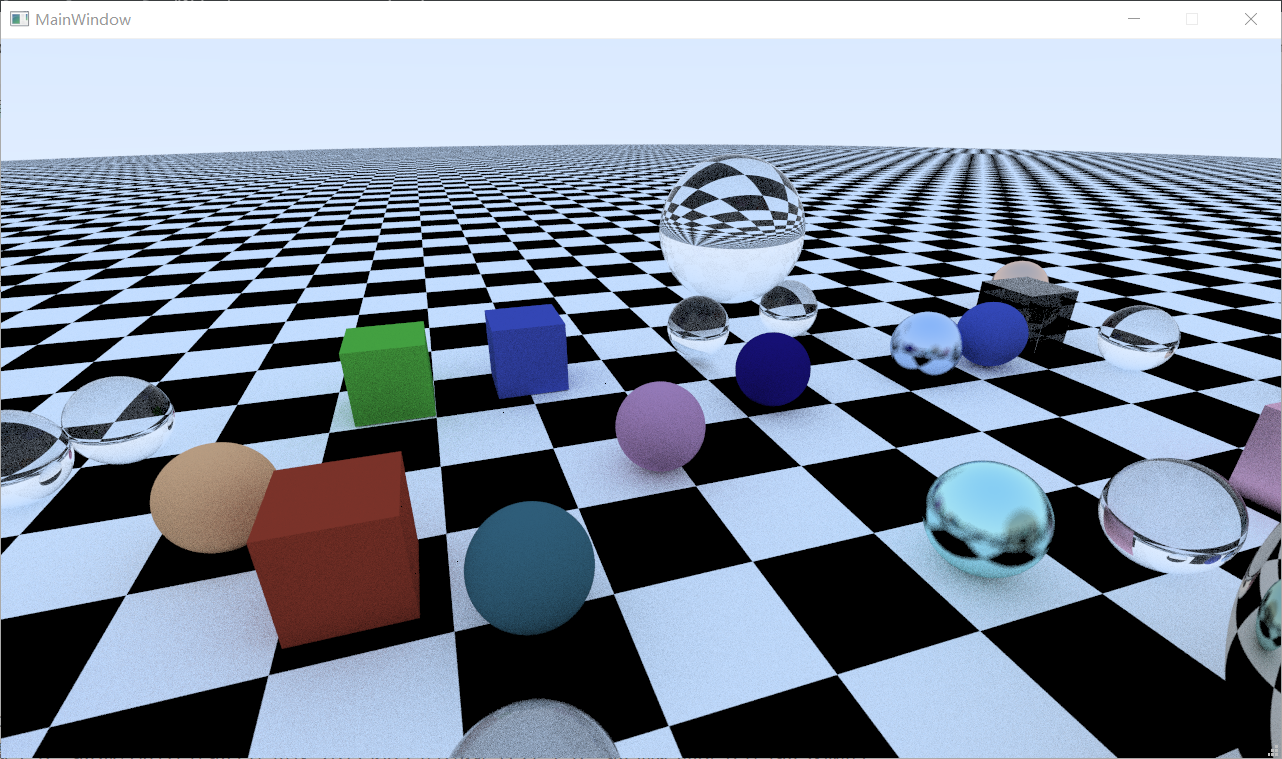
　　当然，这一篇文章实现的是一个极其简易的光追程序，没有性能优化，没有复杂纹理，也没有非常亮眼的效果。这里只是为后期拓展做一个铺垫，打一个底子。之后还会推出进阶篇来实现功能、性能乃至效果更加强大的光追渲染器。

一沙一世界，一花一天堂。君掌盛无边，刹那成永恒。