图像采样的空域频域原理
- 16 5 月, 2021
- by
- pladmin
引言:
采样是处理图像必不可少的一个步骤,同时抗锯齿也是成为当下游戏渲染的一个重要技术,本篇blog的目的便是解析一下它们的原理。
首先,什么是采样?我们想要获取的信号往往是连续的,但实际上我们不可能无间隔地获取实时信号,因此我们只能离散地进行采样。而采样会导致很多问题,例如锯齿(不平滑不圆润)等等走样问题。反走样技术就是要解决这类问题,不过学习该门技术需要一点信号处理的知识。
傅里叶变换:
之前对于采样的原理很抗拒,主要源于对傅里叶变换的抵触。相信大部分搞计算机的同学最开始听到这个词时也头疼不已,但实际上它并没有想象中那样复杂。在分析采样原理的时候,我们无需推导傅里叶变换的公式,只需要了解它代表什么、能做什么即可。
首先引入傅里叶级数展开的概念。对于一个任意的函数,我们都可以用若干个正弦函数来叠加形成。如下图所示,我们给出一个周期性的方波:
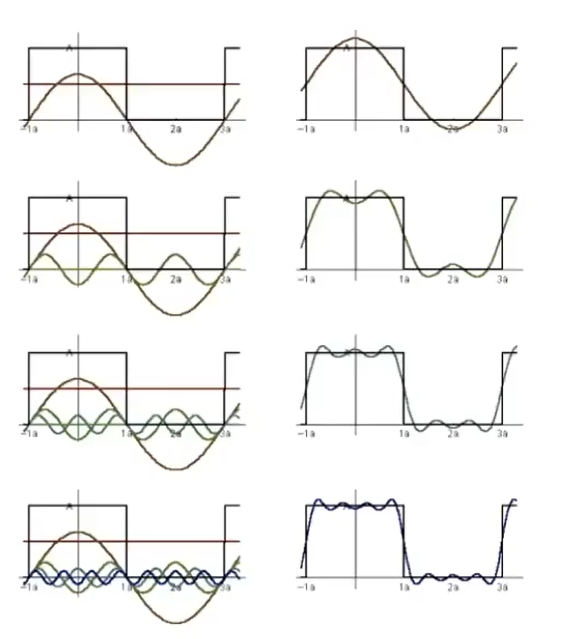
可以看到,为了拟合方波,我们使用了许多不同周期或频率的正弦波来进行叠加。使用的不同频率正弦波越多,最后拟合的效果就越好。对于方波而言,可能需要无限各不同频率的波进行叠加,但这不影响“任意函数都可以由正弦波叠加形成”的结论。那么,为什么是正弦波呢?是因为正弦信号恰好是很多线性时不变系统的特征向量,简而言之就是三角函数的正弦波的所有组合可以叠加出所有信号波的形状,而方波和三角波并不具备这样的特点。
总而言之,对于任意一个函数,都可以由所有频率的正弦波乘上各自的强度后叠加形成,那么关键点在于:各个频率的正弦波的强度怎么求呢?这就要请出我们的傅里叶变换了。
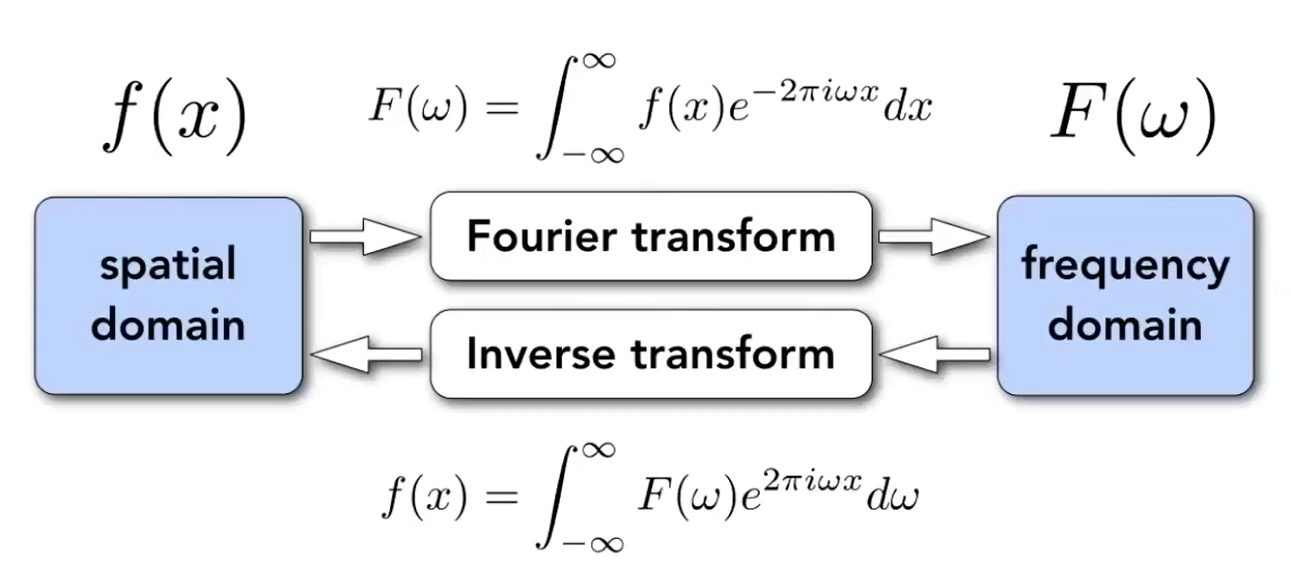
f(x)指的是空域或时域中的原函数,F(w)对应的就是为了拟合f(x),每个频率的正弦波对应的强度是多少,即横坐标是频率,纵坐标是对应的强度,这个就是我们上文想要求的函数。而f(x)和F(w)之间的变换可以通过图中的傅里叶变换公式实现(毕竟不是数学blog,所以就不推导公式了)。下图是一个最简单的例子:组成方波的各个正弦波在频域中的强度分布:
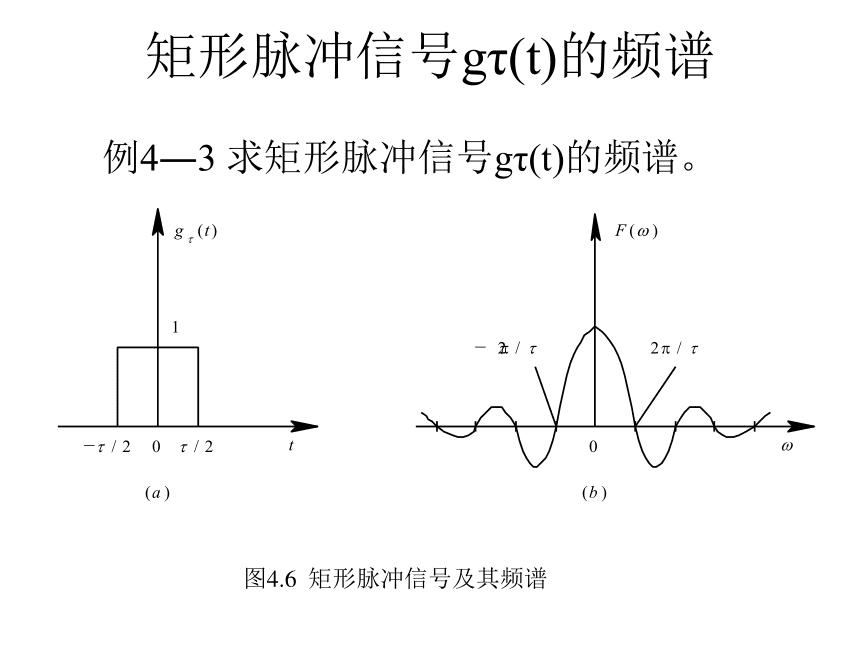
现在我们知道,对于任意f(x)都对应着一个频谱F(w),那么回到我们处理图像的问题上来。对于图像而言,频率代表着什么呢?实际上图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度。举个例子,大面积的沙漠在图像中是一片灰度变化缓慢的区域,对应的频率值很低;而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域,对应的频率值较高,也就是说图像(或者说空域)的频率表示的是灰度值的变化快慢。
那么我们知道图像是一种二维信号,对于最简单的灰度图,我们采样出来的信息应该是f(x,y),那么对应的频谱也会扩充到二维,即F(u,v),表示两个维度上的频谱分布。
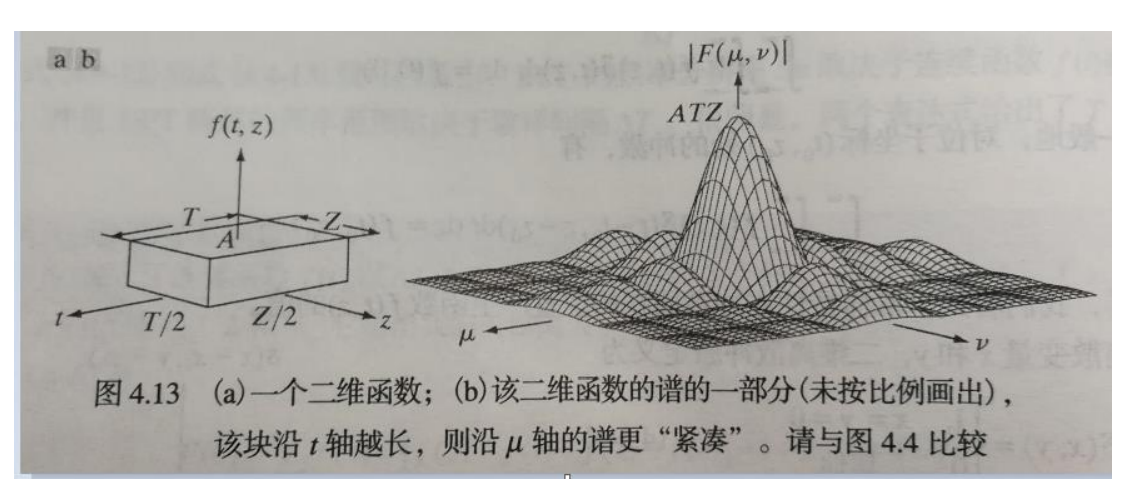
二维的傅里叶变换就更复杂了,所以就不再讨论公式了。为了让f(x,y)和F(u,v)之间的关系更加直观,我们把F(u,v)这个函数图样转换成一张图片,用灰度值来代表对应频率正弦波的强度,这就生成了一张频谱图:

左图是原图,右图是对应的频谱。中间部位非常亮,灰度值非常高,这意味着频率较低的波对应的强度会非常大;频率较高的波对应的强度会非常小。那么现在话锋一转,在此之前我们思考的方向都是,修改原图可以修改对应的频谱图,但是如果我们要修改频谱图来改变图像,会怎么样呢?
频域滤波:
上文提到低频强度很高,高频强度很低,现在我们要探究一下通过修改频谱图来影响图像。首先,我们尝试把中间(低频区域)挖个洞。怎么挖呢,我们定义一个新的频谱函数G(u,v),它的特点是u和v比较小时G(u,v)=0,u和v比较大时G(u,v)=1,让原来的F(u,v)乘一下G(u,v),就完成了低频挖洞操作。它的效果就是让原来的F(u,v)即将低频的波都过滤掉(这个操作叫做高通滤波,即保留高频率的波段,去除低频率的波段)那么图像会变成如下模样:
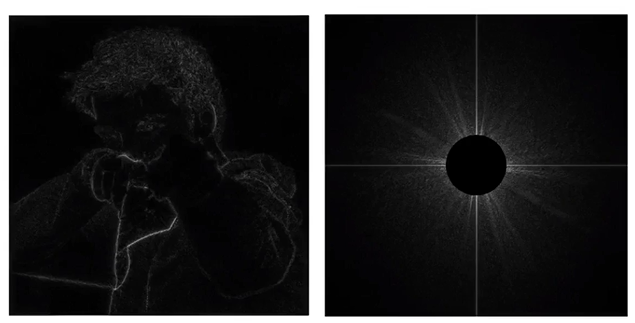
现在左图只剩下一些边缘了。为什么会这样呢,因为对于一个图像而言,若某区域中其灰度值变化很缓,类比到时域就是信号变化很缓,换言之就是信号周期很长。信号频率与信号周期成反比,因此该区域对应的就是低频率的波段。将这些波段滤掉,那么灰度值变化不大的区域就会被滤掉;而边缘最大的特点就是突变,即信号变化非常快,频率更高。在滤波过程中,高频波被保留了下来,因此原图中的边缘也会被突出了。
那么反过来,如果我们过滤掉高频波,保留低频波,就会将原图变为这样:

按照上面的逻辑,边缘这些对应高频波的部分都会被过滤掉,体现在图像上就是变平滑了、变模糊了。要注意的是,这就是反走样的关键所在:将尖锐突出的边缘或锯齿平滑处理,使得其周围变得模糊且柔和。
接下来我们要考虑的问题就是如何把图像这种二维信号变换到频域当中。对于一张图像,如果要将它变换到频域空间,就需要对图像这种离散的二维信号进行变换,这里我们就要用到大名鼎鼎的DFT(离散傅里叶变换):
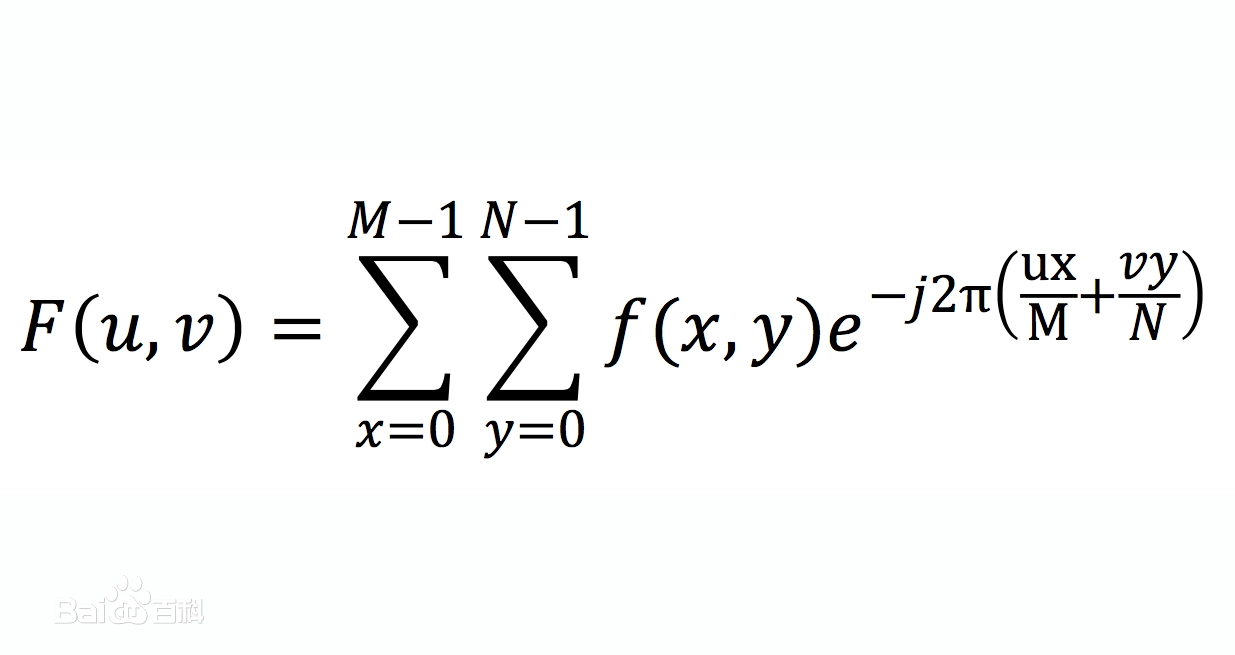
不难想象,dft的算法复杂度是O(n^2),这样一张1080P的图片恐怕要跑个几天甚至几个月才能出结果,显然是无法接受的。因此我们可以引入快速傅里叶变换FFT:
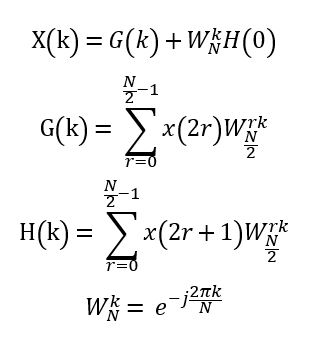
它的算法过程其实类似于归并算法,即每次二分,分而治之,最后再按照逆方向归并回来。和归并排序类似,算法复杂度是O(nlogn)。归并方法如下图所示:
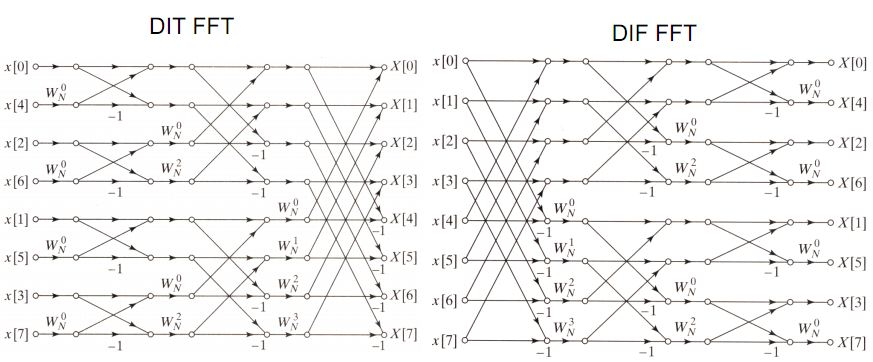
(实话实说,我是挺惊叹于这种算法的发明的。自己能根据公式顺着能推下来,但无法想象在什么都没有的情况下是如何发现并研发出这种算法的)
不过还是要说,FFT的时间复杂度虽然比DFT有所优化,但这种代价依然是非常高的,而且滤波之后还要进行反变换,一来一回会耗费非常多的性能。因此,我们必须要将滤波的操作搬到空域来解决。接下来我们就要求一下,空域中要怎么操作才能等效于频域中的滤波操作。
现在我们假定要完成低通滤波操作,设P是对空域进行滤波操作,Q是对频域进行滤波操作,那么P(f(x,y))=Q(F(u,v))。现在我们已知f(x,y),可以通过DFT算得F(u,v),Q操作上文已经解释过了,就是让F(u,v)乘一下G(u,v),现在我们要求出P操作是什么。这里我们直接引用一个定理:空域卷积等于频域乘积 空域乘积等于频域卷积。
这就意味着:f(x,y)卷积{G(u,v)}-1=F(u,v)*G(u,v),即原图像与低通滤波器的傅里叶逆变换进行卷积,等于图像的频域表示与滤波器相乘。这也说明了,P操作就是和滤波器的逆傅里叶变换作卷积操作。事实上,为了节约成本,我们不会先构造出来G(u,v)再作DFT变换为{G(u,v)}-1,而是根据经验直接构造卷积核,来完成卷积操作。
空域卷积:
上文提到了,在空域进行低通滤波的方法是进行卷积。卷积怎么理解呢,本质上就是让信号中的孤立点获取周围信息。卷积的式子如下:
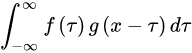
其中f是原函数,g则是卷积核。图像处理一般没有连续函数卷积的情况,因此我们可以直接来看离散卷积。首先举个一维卷积的例子:
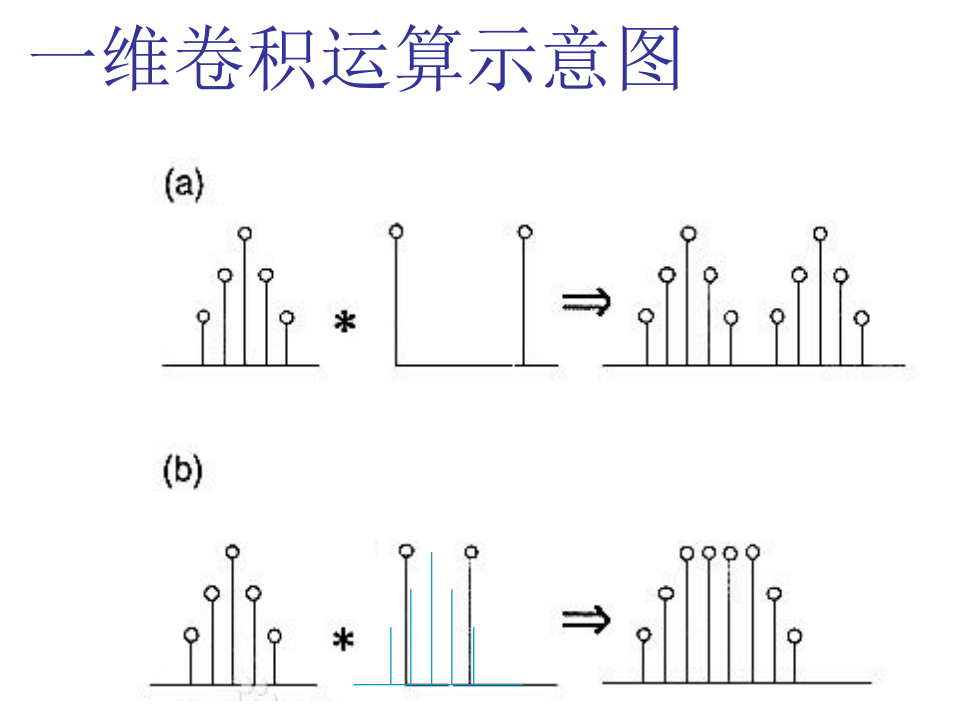
如果大家还是比较迷糊的话,可以看以下二维卷积的例子:
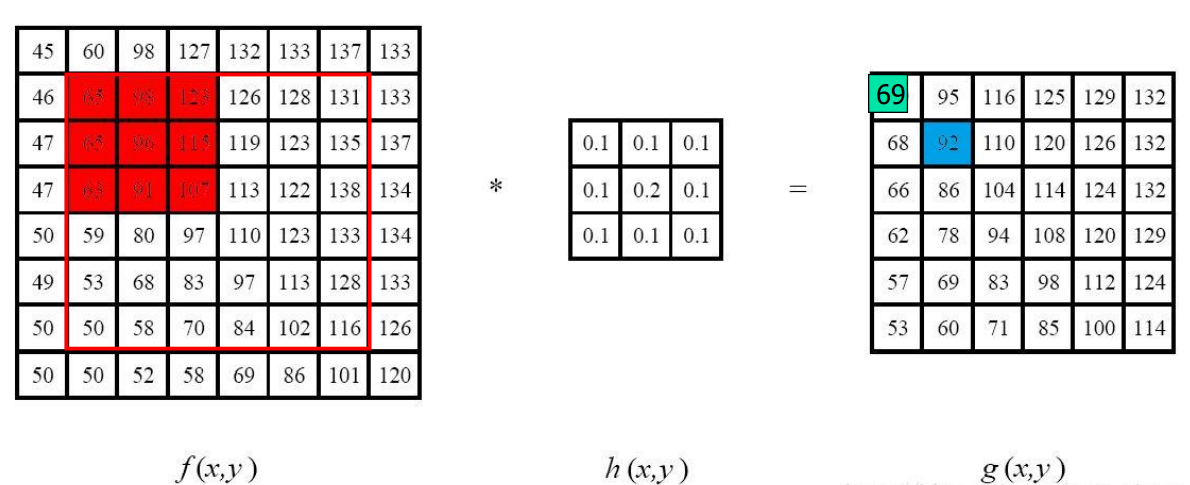
对于f(x,y)中的每一个点,以此为中心,把h(x,y)贴进来进行乘积加和,最后结果写入这个点中。举个例子,对于f中第三行第三列的96,卷积就是0.1*65+0.1*98+0.1*123+0.1*65+0.2*96+0.1*115+0.1*65+0.1*91+0.1*107=92,然后将92写入原来的这个点。
所以卷积的本质上,就是按照一定的权重将周围点的信息混合到中心点中。对于非边缘部分,由于其像素灰度较为接近,因此卷积前后不会有什么变换;对于边缘部分,它在卷积的时候会把边缘外的信息糅合进来,从而失掉边缘的突变性,实现整体平滑和模糊。所以卷积操作比较便于计算,也好理解,因此在做平滑处理的时候我们一般都使用空域卷积的方法。
那么如何构造低通滤波的卷积核呢?首先要做到所有权重都是正数,如果有负数的话会趋向于高通滤波;其次就是卷积核必须要归一化,即卷积核内的权重之和必须为1,否则卷积后的颜色会严重跑偏。如下图所示:

常见的卷积核有:所有权重都一样的均值滤波,呈二维正态分布的高斯滤波等。平滑程度取决于权重设置,平滑范围取决于卷积核的大小。现在已经明确了空域卷积和频域滤波的关系了,那我直接上一张闫老师的图来复习一下:
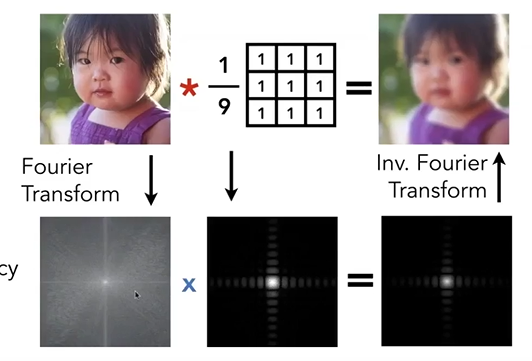
这里大家也能看到中值卷积核在频域中的滤波器图样。
空域和频域的采样:
上文讲了卷积和滤波操作的原理,它们其实都是反走样的手段。但是反走样的前提是先进行采样,所以接下来我们来看一下采样的原理。先看下图中的左半边:
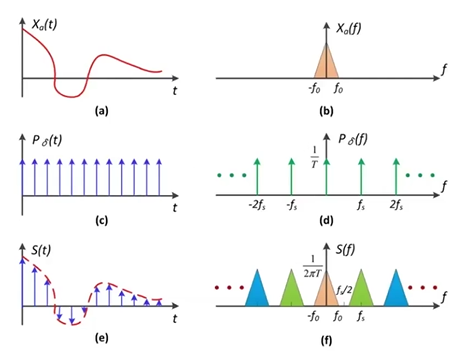
对于一个连续的信号函数,我们要采样一些离散的信号点,此时我们需要用到冲激串函数(图c):它的特点是每隔一段固定时间做一次冲激(这里还会有一段略显复杂的数学推导,这里直接略掉了)我们只需要将原信号函数和冲激串函数进行相乘,即可得到离散的采样点。
那么,空域或时域中的采样,对应到空域中是什么样子呢?我们前面提到了,空域的相乘也等于频域的卷积,因此原函数和冲激函数相乘,就等于原函数的频域表示与冲激串的频域表示进行卷积。冲激串的频域如图d所示,那么按照我们前面提到的卷积原理,就会得到图f的样子:多个图b排列在一起,在坐标轴上两两相隔的距离相等。
那么我们从这个角度来理解走样与反走样:走样的本质,就是图f中的各个图b之间出现了重叠部分。此时我们若先对图b进行低通滤波,使得图b在坐标轴上的宽度削窄,此时再进行采样,它们便不再发生重叠,解决了走样问题,这就是反走样。
如图a就是典型的频域中走样现象,那么为了避免这个现象,我们需要在采样之前对原频谱进行低通滤波,变成图b:
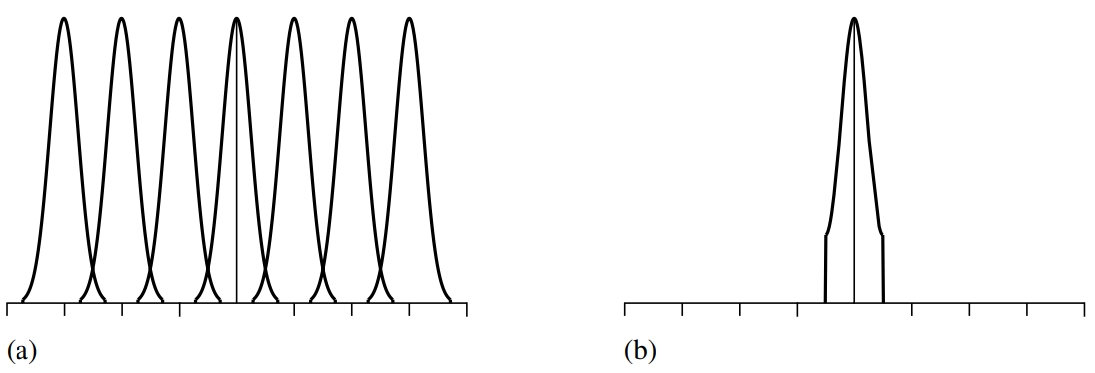
所以我们从空域和频域两部分分析了,为什么空域卷积和频域滤波可以解决走样问题:空域卷积能够平滑边缘,柔化图像;频域滤波能够解决原函数的频域采样后发生的重叠问题。这里一定要注意:必须先进行卷积或滤波,再进行采样。大家可以想一下,对于频域而言,如果先采样再滤波,那么重叠的部分依旧会存在,无法完成反走样;对于空域而言,如果先采样再卷积,那么在卷积之前锯齿已经出现了,此时再进行卷积已于事无补。所以先卷积滤波后采样的顺序一定要记住!
由于本篇文章篇幅过长,因此没有详细介绍反走样技术的代表MSAA算法,之后我会在学习完FXAA和TAA后,把三项反走样技术放在一篇文章中介绍。